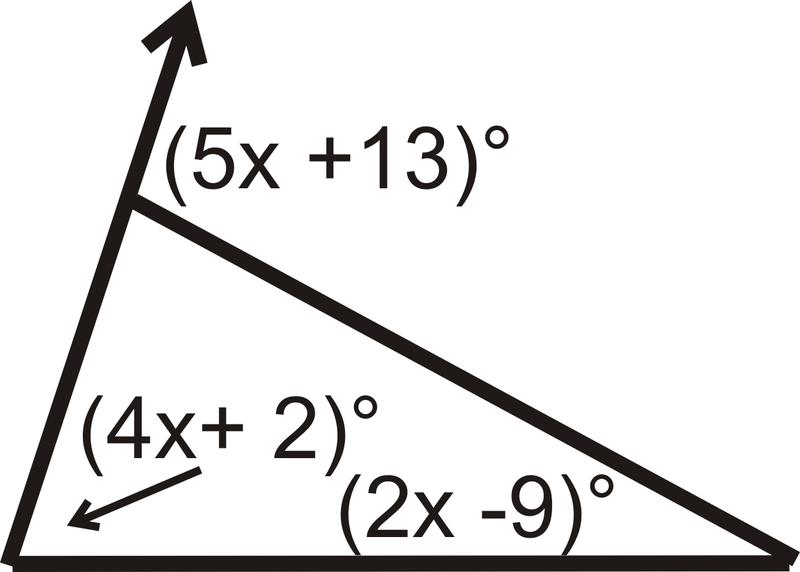Solve for x

x = 109
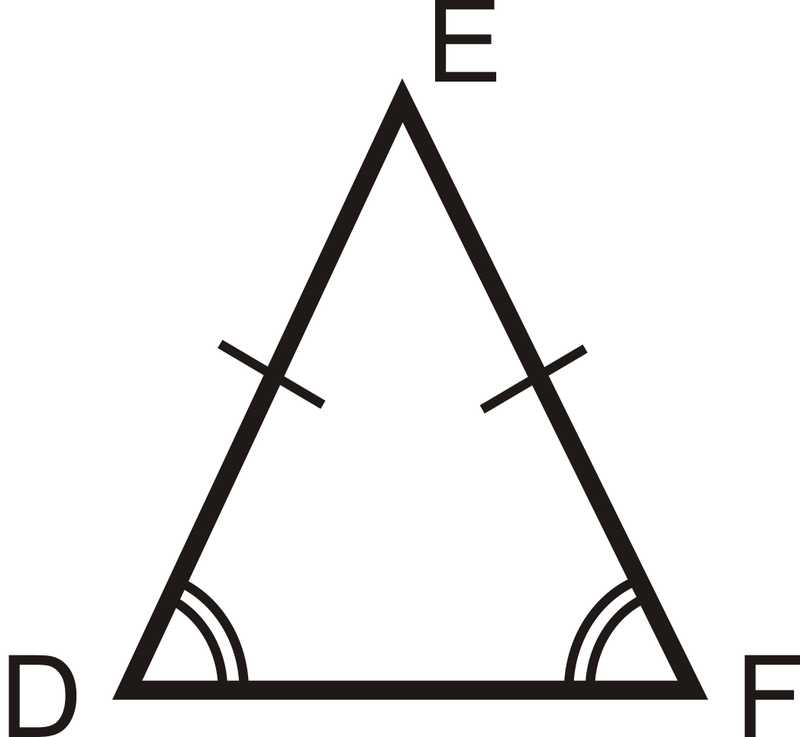
Name a pair of congruent sides
Acceptable Answers
AB and DE
BC and EF
CA and FD
Solve for x
x = 4
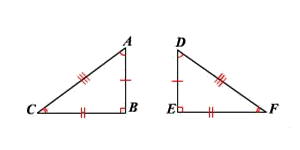
Are these two triangles congruent? If so, by which theorem?

Yes, by SSS
x = 20
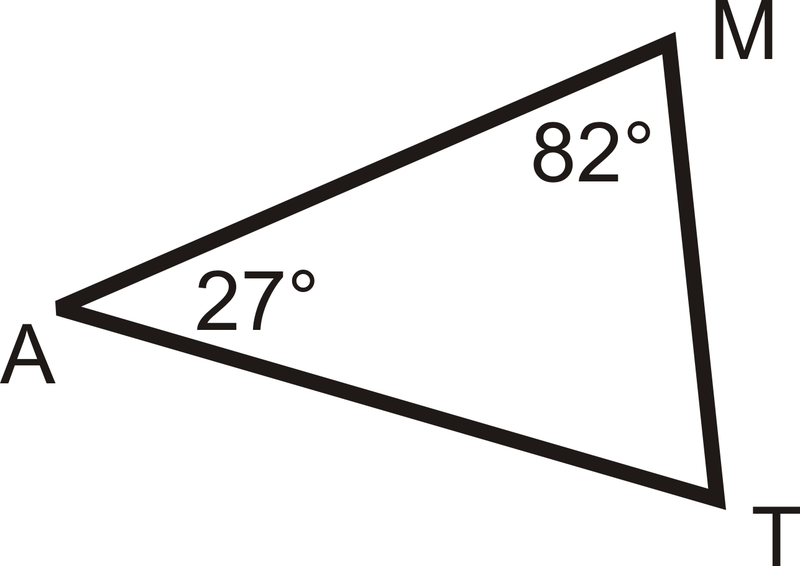
Solve for the missing angle
T = 71 degrees
Name a pair of congruent angles

Acceptable Answers
Angle A and Angle D
Angle B and Angle E
Angle C and Angle F
Solve for a if DE = 5a - 3, EF = 2a + 6, and DF = 7a - 12
a = 3
Are these triangles congruent? If so, by which theorem?
Yes, by ASA
Solve for x: Angle 1 = 7x + 12, Angle 2 = 3x + 14, Angle 3 = 3x - 15
x = 13
Solve for y
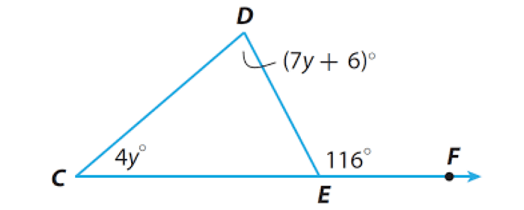
y = 10
If ABCD is congruent to EFGH and AB = 3x + 4 and EF = 25, solve for x

Solve for x and y
x = 25
y = 4
Can you prove these two triangles are congruent? By which theorem?
Yes, by HL
Segment AB = 13x - 4, Segment BC = 9x + 24, Segment AC = 6x + 2
x = 7
Solve for x AND classify the triangle by its angles.
x = 9
Acute Triangle
Solve for x if we assume BAHG is congruent to DCFE
NOTE: 4x + 5 is on Angle H
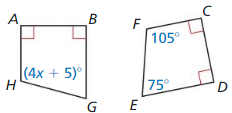
x = 25
Solve for x
NOTE: Line GF should say 3x + 10
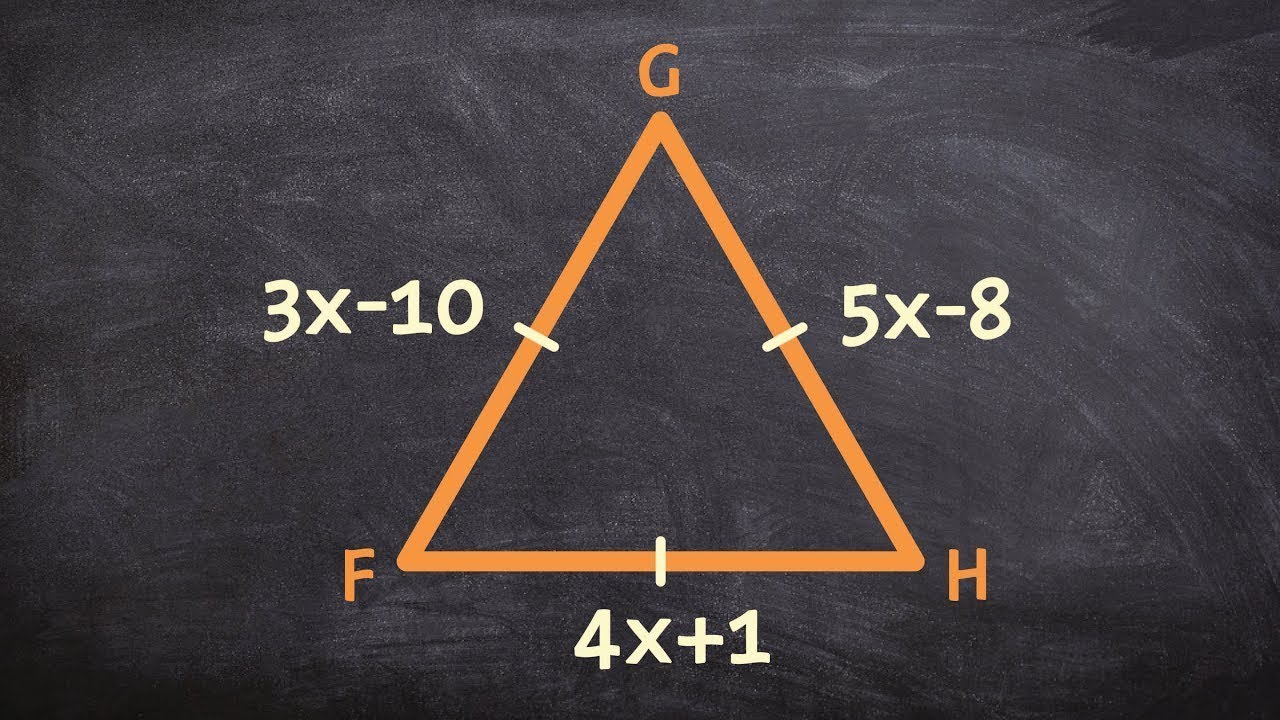
x = 9
Write a congruent statement and state the theorem
1) Answers may vary
2) By AAS
Are they congruent? Prove it

Yes, by SSS
Solve for x
Write a congruent statement of the image below

Answers may vary
Assume: Triangle ABC is congruent to Triangle DFE
Solve for x and y

x = -12
y = 13
Give a congruent statement to the two triangles and identify the theorem that makes the two congruent.
1) Answers may vary
2) by ASA
Fill in the blank
Corresponding
P ____________ of
Congruent
T ____________ are
C ____________
Parts
Triangles
Congruent