Graph Basics
Graphs
Trees/networks
Paths/Walks, etc.
Miscellaneous
100
What are the points/dots of a graph called
Vertices
100
What 2 things must a graph have
Vertices and edges
100
A tree contains no: (3 things)
Loops
cycles
multiple edges
100
A trail is a walk with:
no repeated edges
100
What is the highest degree of any node in the diagram?
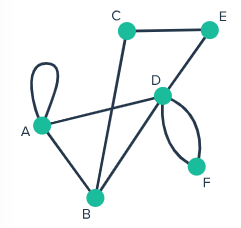
Node D - Degree 5
200
What are the lines of a graph called
Edges
200
A connected graph is when:
Every vertex is connected directly or indirectly
200
a tree with 3 vertices has ____ edges
2
200
A path is a walk with no repeated:
vertices
200
How many edges are there in this network?
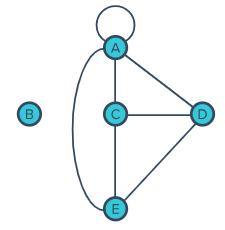
7 edges
300
The degree of a vertex represents:
The number of edges attached to a vertex
300
2 or more edges that connect the same vertices are called
Multiple edges
300
A spanning tree connects:
all vertices
300
A circuit must:
start and finish at the same vertex
300
What is the length of the shortest path from A to H
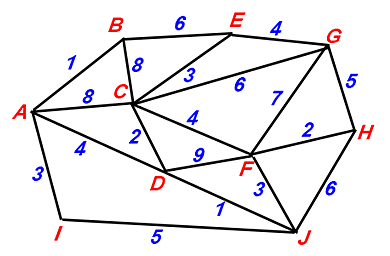
What is 10, A - D - J - F - H
400
A loop contributes ___ edges to a vertex
2
400
2 graphs are isomorphic
they have the same number of edges & vertices
and
the vertices have the same degree and edges connect to same vertices
400
The numbers on a network are often used to represent.. (provide an appropriate example)
Cost, distance, time and other appropriate
400
The difference between an eularian circuit and an eularian trail is:
a EC must have all even degree vertices
400
For a network with 5 nodes, this is the size (or dimensions) of its adjacency matrix
A 5 x 5 matrix or 25 fields
500
The sum of degrees is equal to ______ the number of edges
Twice
500
A planar graph must be draw with no:
intersections
500
The shortest path is used for finding:
shortest distance or time
500
A traversable graph must have either ____ or ______ vertices of odd degree
zero
two
500
This type of graph can be drawn on a flat surface without any edges crossing over each other.
What is a planar graph?