Limits
Derivatives
Derivative Applications
Integrals + Applications
Surprise!
100
lim_{x to 4} f(x)
Check left and right on the function to see if they match.
100
Find the derivative.
f(x) = 3 ln(x) +4/(sqrt(x^3)) -e^4 + arcsec(x)
Basic and power rules
100
Given f(x) = x^2 +5x-1 , find the equation of the tangent line at x=3 and find the linear approximation of f(3.1) .
Take the derivative. Plug in 3 to get slope at x=3. Plug 3 into function to get y-value. Plug both into point-slope form to find equation of the tangent line at x =3.
Plug 3.1 into equation of line found in first part to get linear approximation.
100
int ( 3/sqrtx + 5/x - 4e^x + 2 cos x - pi) dx
Basic and power rules. Don't forget +c!
100
Find the derivative of
f(x) = int_-3^tanx u/(u^3 -5) du
FTC Part 1! Take off the integral, plug in the tanx, then multiply and take the derivative of tanx.
200
lim_{x to -3} (t^2 -9)/(2t^2+7t+3)
Plug in, 0/0, algebra and cancel.
200
Find the derivative.
f(x) = (x sinx)/(1+x)
Quotient and Product Rules
200
Find the absolute extrema of f(x) = x^3-3x^2+1 on the interval [-1/2, 4] .
Find critical points: take derivative, set equal to 0 and solve.
Plug critical points and end points into function to see which has the greatest and least y-value.
200
Given int_-1^6 f(x) = 7 , int_-1^3 f(x) = 2 , and int_3^6 g(x) dx = -3 , find
int_3^6 (5f(x) -g(x) +4 )dx
Use additivity to find int_3^6 f(x) dx , then break up the addition/subtraction and constant multiplier, and use
int_a^b c dx = c(b-a)
200
Use the limit definition of derivative to find the derivative of
f(x) = x^2+2x-1 .
lim_{h to 0} (f(x+h) - f(x))/h
300
lim_{x to 0} (x-5)/(x^4)
Plug in, number over 0, vertical asymptote -> check both sides!
300
Find the derivative.
f(x) = sqrt( (cotx - lnx)/(x^2+3x)
Chain Rule!
300
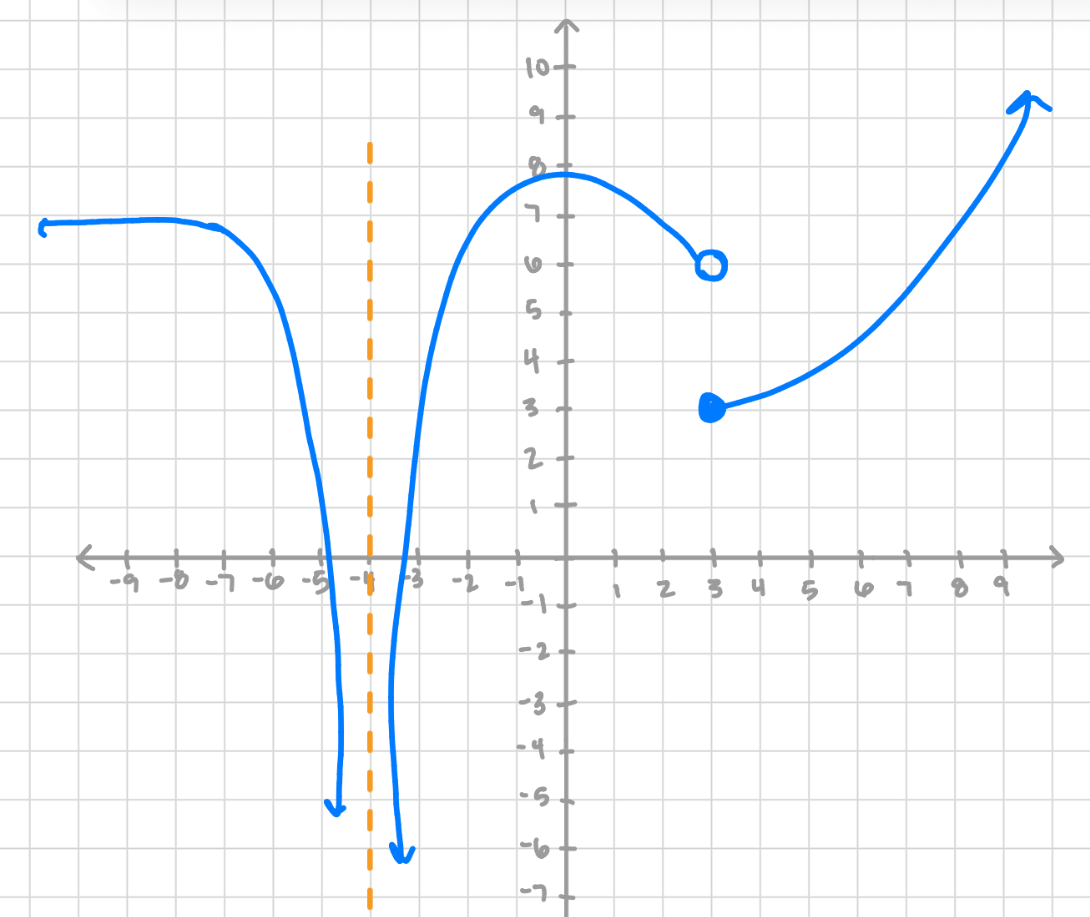
Sketch the curve given the info:
Domain:
(4, 10) \cup (10, oo)
lim_{x to oo} f(x) =1 , lim_{x to 10^+} f(x) = -oo , lim_{x to 10^-} f(x) = oo
f(5) = 0, f(11) =0, f'(12) = 0, f''(15) = 0
f'(x) > 0 when x is in
(4, 10) \cup (10, 12)
f'(x) < 0 when x is in
(12, oo)
f''(x) > 0 when x is in
(4, 10) \cup (15, oo)
f''(x) < 0 when x is in
(10, 15)
Domain gives overall check.
HA on right at 1.
VA at 10, going up on left and down on right.
x-intercepts at 5 and 11.
Increasing from 4 to 10 and 10 to 12. Decreasing greater than 12. Local max at 12.
Concave up 4 to 10 and greater than 15. Concave down between 10 and 15. Inflection point at 15.
300
Find the area bounded by y = f(x), x = -1, x = 1, and the x-axis, where
f(x) = 1/ \sqrt(1-x^2)
Set up integral and solve!
300
Determine if the function is continuous at x = 1.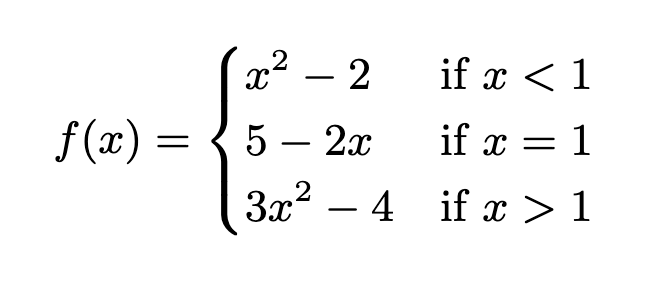
If it is continuous, verify all conditions of continuity. If it is discontinuous explain why.
Need to check
1. Limit exists (left = right)
2. Function value exists
3. Limit and function value are equal
400
lim_{x to - oo} (e^(3x) - e^(-3x))/(e^(3x) + e^(-3x))
Limit at infinity, will get (- oo)/(-oo), could try L'Hospital's (wouldn't work), need to use algebra and true facts.
400
Find the derivative.
f(x) = ((x+1)/(x-1))^cosx
Logarithmic Differentiation
400
If 1200 sq cm of material is available to make a weird cylinder package with a circular base and an open top, find the largest possible volume of the package.
Optimization. Set up two equations one of surface area (known-constraint equation) one of volume (unknown-optimization equation). Use constraint equation to get optimization equation in one variable. Take derivative of optimization equation, set it equal to zero, and solve.
400
The velocity of a sprinter is given by the table.
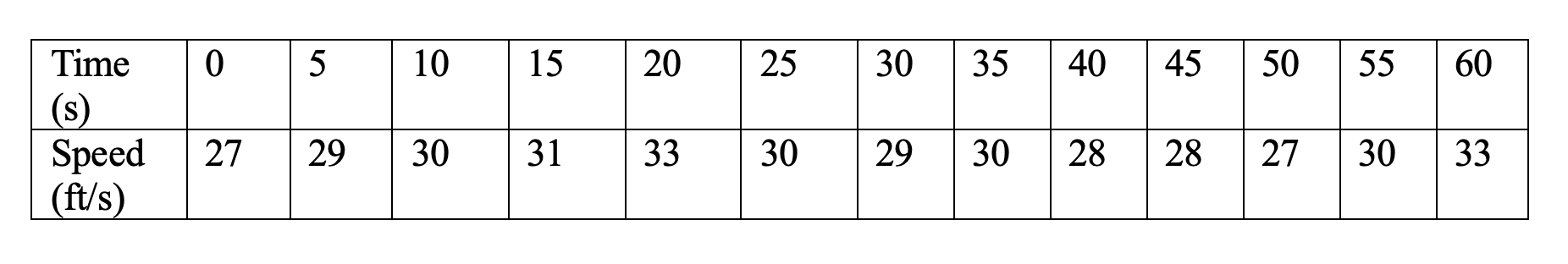
Use a Riemann Sum with 6 subintervals and midpoints to estimate the distance traveled by the sprinter.
6 intervals would give us a width of 10 seconds and midpoints would give the time values t = 5, 15, 25, 35, 45, 55.
So we'd sum the speed values for those times and multiply by 10.
400
Suppose that
4 \leq f'(x) \leq 8
for all x. What's the largest possible distance between f(2) and f(10)?
Mean Value Theorem!
500
lim_{x to 0} (cosx)^csc x
Use logs to bring down exponent, then write as a fraction, then use L'Hospital's Rule.
500
Find the derivative.
x^2y^5 + cos (2x+3y) = 11x^2 - e^y
Implicit differentiation.
500
A water tank has the shape of an inverted circular cone with base radius 2 m and height 4 m. If water is being pumped into the tank at a rate of 2 cubic meters per minute, find the rate at which the water level is rising when the water is 3 m deep.
The volume of a circular cone is
V = 1/3 pi r^2 h
Related Rates!
Draw a picture and label everything that you can.
Identify what is changing.
Take the derivative of the equation, making sure that anything changing is derivative implicitly with respect to time.
Plug things in and solve.
500
int_0^{pi/3} sinx \cdot e^cos x dx
U-sub! Make u = cos x.
500
Express the definite integral
int_1^4 (2x^2-5) dx
as a limit of a Reimann sum using right endponts.
Need to find \Delta x = (b-a)/n , x_i = a + i \cdot \Delta x , and f(x) .
Then plug into
lim_{n to oo} \sum_{i = 1}^n f(x_i) \Delta x