Parallel and Perpendicular Lines
Angles
Quadrilaterals
Transformations
Congruence Statements
Proofs
Anything Goes!
100
Define parallel lines AND perpendicular lines.
Parallel: Lie in the same plane and never intersect.
Perpendicular: Intersect to form RIGHT ANGLES.
100
Congruent means _______.
Supplementary means _______.
Equal
Add up to 180o
100
Find the measure of <A.
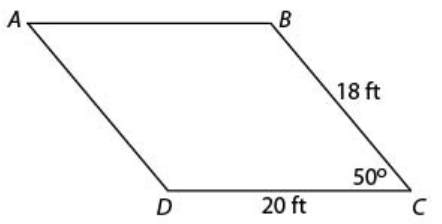
<A = 50o
100
List the transformations that are also rigid motions.
Translation, rotation, reflection.
Preserve congruence.
100
What side is congruent to side EG?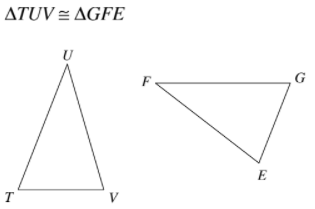
Side VT
100
Complete the proof below.
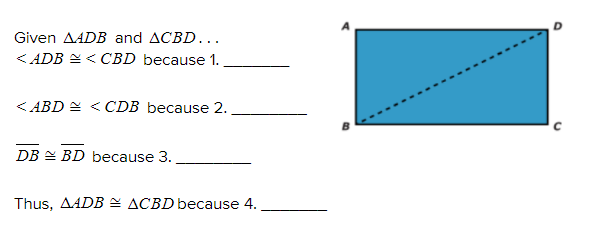
1. Alternate interior angles are congruent
2. Alternate interior angles are congruent
3. Reflexive property
4. ASA
100
What is the rotational symmetry of a regular hexagon?
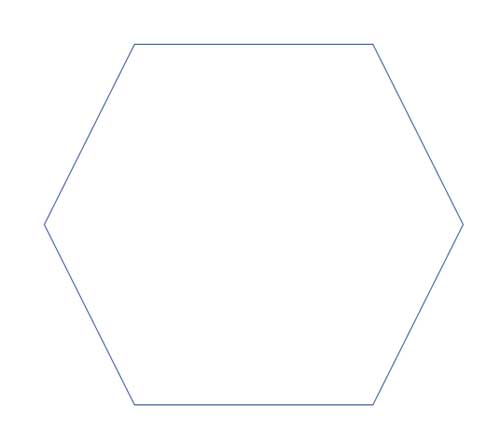
360/6=60
200
Parallel lines have slopes that are ___________, while perpendicular lines have slopes that are _________.
Equal; Opposite reciprocals.
200
What angles are congruent to <1?
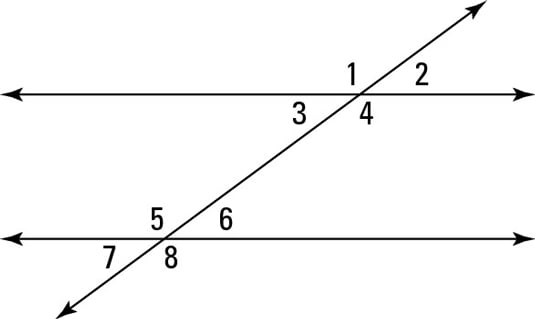
<4, <5, <8
200
Find the measure of <D.
<D = 130o
200
Translate the point A(-4, -4) by (x + 3, y + 4).
A'(-1, 0)
200
What angle is congruent to <FED?
<RSD
200
Complete the proof listed below.
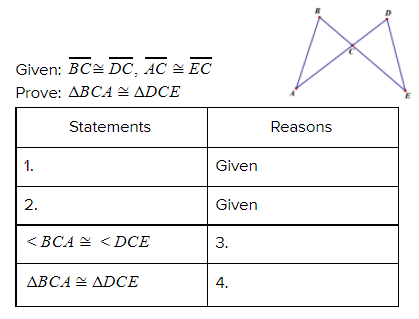
1. BC ≅ DC
2. AC ≅ EC
3. Vertical angles are congruent.
4. SAS
200
Solve the equation.
4x-3=65
x=17
300
Identify the slope and y-intercept of the following line:
y=-6x-2
m=-6;b=-2
300
Identify the angle relationship.
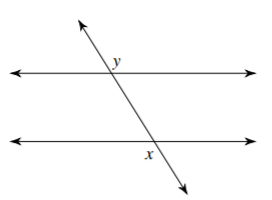
Alternate exterior angles
300
Solve for x.
x=0
300
If B(3,1) and B'(-4, 5), what is the translation vector?
< -7, 4>
300
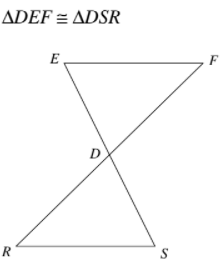
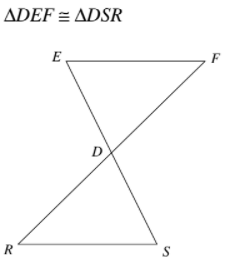
Write the six corresponding congruent parts of the triangles shown below.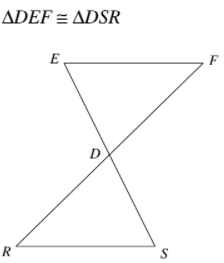 
DE≅DS; EF≅SR; DF≅DR; <DEF≅<DSR; <EFD≅<SRD; <FDE≅RDE
300
Complete the proof listed below.
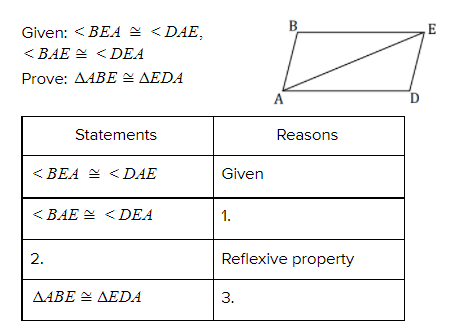
1. Given
2. AE ≅ EA
3. ASA
300
8/7 +4/3=
52/21
400
Write the equation of a line that passes through the point (-1,3) and is parallel to the line below.
y=-6x-2
Slope of original line: -6
Slope of new line: -6
Plug -6 and the points (-1, 3) into y=mx+b
y=-6x-3
400
Find the value of the missing angle.
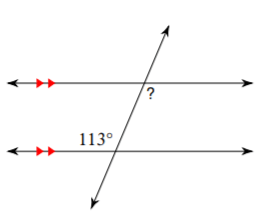
113o
400
Find the value of x.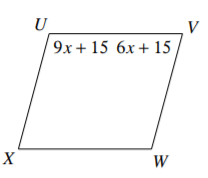 
x = 10
400
Reflect the triangle M(2,0), E(3,1), L(-1,2) about the line x= -3.
M'(-8,0); E'(-9,1); L'(-5,2)
400
Label the corresponding congruent sides and angles on the triangles below.
400
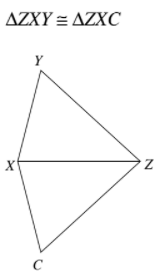
Complete the proof below.
1. Given
2. CB || AD
3. <ADC ≅ <CBD
4. Alternate interior angles are congruent
5. BD ≅ DB
6. AAS
400
4/5+1/2+5/4=
51/20
500
Write the equation of a line that passes through the point (12,1) and is perpendicular to the line below.
y=-6x-2
Slope of original line: -6
Slope of new line: 1/6
Plug 1/6 and the points (12, 1) into y=mx+b
y=1/6x-1
500
Find the value of x.
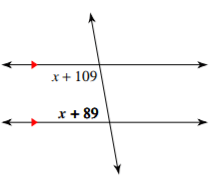
x=-9
500
What property tells us that side AC is congruent to itself?
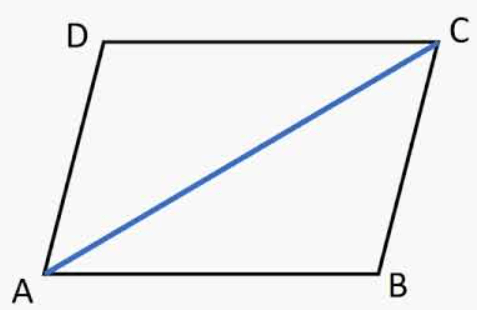
Reflexive property
500
Dilate Z(-1, 0), G(0, 2), E(1, 3), W(-1, -1.5) by a scale factor of 2.5.
Z'(-2.5, 0); G'(0, 5); E'(2.5, 7.5); W'(-2.5, -3.75)
500
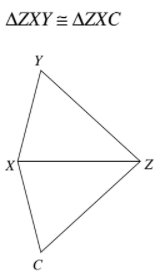
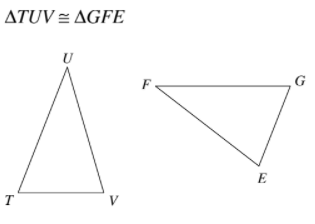
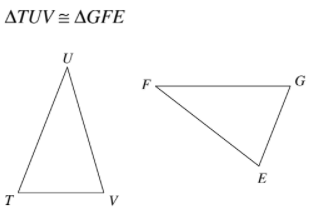
Label the corresponding congruent sides and angles on the triangles below.
500
Complete the proof below.
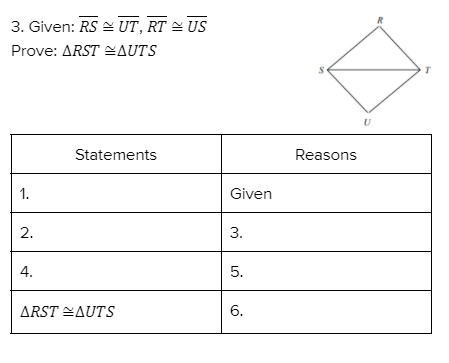
1. RS ≅ UT
2. RT ≅ US
3. Given
4. ST ≅ TS
5. Reflexive property
6. SSS
500
How many squares are there?
14 squares
600
Is the line passing through the points (−4,5) and (1,10) parallel to the line passing through the points (−18,−6) and (−8,4)?
m=1
m=1
Since the slopes of the lines are the same, the lines are parallel.
600
Find the value of x.
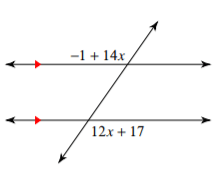
x=9
600
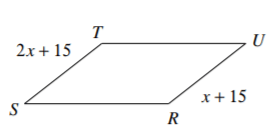
Name one characteristic of ALL parallelograms.
- Opposite sides that are parallel.
- Opposite sides are congruent.
- Opposite angles are congruent.
- Consecutive angles are supplementary.
600
Rotate the following points 180° clockwise about the origin: L(1, 3), Z(5, 5), F(4, 2).
L'(−1, −3); Z'(−5, −5); F'(−4, −2)
600
Label the corresponding congruent sides and angles on the triangles below.
600
Complete the proof below.
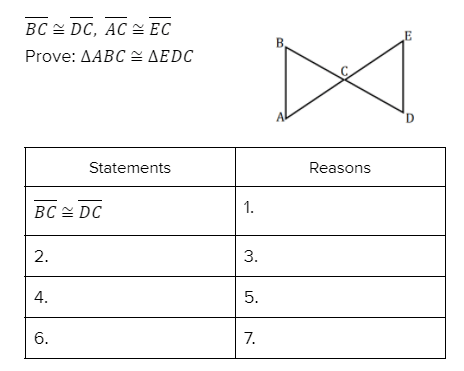
1. Given
2. AC ≅ EC
3. Given
4. <BCA ≅ DCE
5. Vertical angles are congruent
6. Triangle ABC ≅ Triangle EDC
7. SAS
600
There are five people in a meeting. Every person wants to shake the hands of everyone else in the room once. How many handshakes will occur?
10 handshakes