The order in which the dimensions of a matrix are listed
rows x columns
The type of graph that quadratics produce
Parabolas
What is the solution to any system of two equations?
Their intersection point
Name the given polynomial 3x5 - 54
Quintic Binomial
Increasing and decreasing intervals are described with these values.
x-values
Roots, zeros, solutions, are all names for what?
x-intercepts
This tells us the maximum number of possible rational roots.
Degree
What has to be true in order to multiply two matrices together?
Columns of the first must match the rows of the second
Two complex numbers, in the form a + bi, that when multiplied always result in a real number
Complex Conjugates
Place the following in slope-intercept form
6x+2y=22
y=-3x+11
Simplify x2+6x-10 - (-2x2+5x)
3x2+x-10
Determines if the graph will cross or bounce at a given root.
Multiplicity
Identity Matrix
This theorem tells us that if 3+i is a root, so is 3-i
Conjugate Root Thm
Draw the additive identity for a 3x4 matrix.
3x4 zero matrix
Solve with square roots. Don't forget +/-.
2x^2+42=6
+- 3isqrt2
Solve the equation 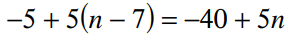
All real numbers
3(2x +1)(4x +5)
24x2 + 42x +15
State the end behavior for the given function without graphing it:
-3x^7+5x^3-12x-100
x --> infinity f(x) --> -infinity
x --> -infinity f(x) --> infinity
The simplest form of any function in a given group of functions.
Parent function
List the possible rational roots
x^5-8x^3+2x^2-12
{(+/- )12, 6, 4, 3, 2, 1}
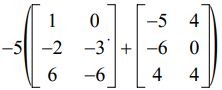
See Ms. Rogers
Factor and solve: x2 + 5x = -6
(x + 2)(x + 3) = 0 ; {-2, -3}
Solve the equation
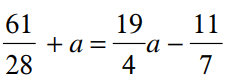
(x2 -5)(x2 + 2x + 1)
x4 +2x3 -4x2 -10x - 5
f(x) = x2 + 3 and g(x) = 6x - 1 find:
(f x g)(x)
6x3 -x2 + 18x - 3
State the domain and range in interval notation.
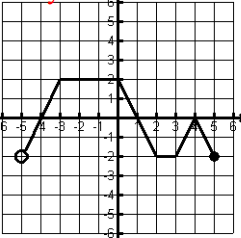
D: (-5,5]
R: [-2,2]
Given f(x), find f(-3)
f(x)=x^5-3x^3+12x^2-14x+1
f(-3)=-11
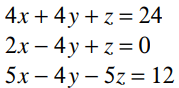
(4,2,0)
Simplify
(4-5i)/(2-i)
(13-6i)/5
Solve the literal equation
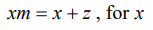
x=z/(m-1)
Factor the following completely.
10x^3-55x^2+60x
5x(2x-3)(x-4)
The height of a model rocket being launched is modeled by the function below. State what each coefficient and constant represent in context. h = feet, time = seconds
h(t)=-16t^2+90t+2
-16 = gravity
90 = initial velocity
2 = initial height
Which parent function is shown?
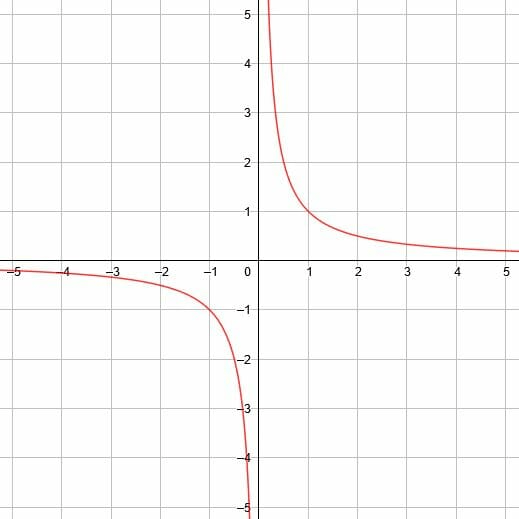
Reciprocal function
Write a 4th degree polynomial equation with integral coefficients that has 2i and 1+i as solutions.
x^4-2x^3+6x^2-8x+8=0
Yellowstone National Park is a popular field trip destination. This year the senior class at High School A and the senior class at High School B both planned trips there. The senior class at High School A rented and filled 8 vans and 5 buses with 420 students. High School B rented and filled 10 vans and 10 buses with 750 students. Every van had the same number of students in it as did the buses. How many students can a van carry? How many students can a bus carry?
Van: 15
Bus: 60
Solve using the quadratic formula
10x^2-4x+10=0
(1+-2isqrt6)/5
The sum of three consecutive odd integers is 17 less than four times the smallest integer. Find the largest integer.
27
f(x) = x2 + 3 and g(x) = 6x - 1 find:
f(g(x))
36x2 -12x +4
A polynomial has a root at 3 with a mult. 2, a root at 0 with a mult. 1, and a root at -1 with mult. 3. Write a polynomial in factored form that could represent this function.
f(x) = x(x-3)2(x+1)3
Factor the following completely
2x^5-14x^3+12x
2x(x-1)(x+1)(x^2-6)
Solve.
x={-1,2,(3+-sqrt17)/2)