Similar Figures
Dilations and Scale Factor
Slope
Triangles
Vocabulary
100
Identify all the figures similar (remember congruent can be similar) to polygon A.
D, E, and F.
100
What would happen to a figure if it was dilated to a scale factor of 1/2?
The sides would be half the size they used to be.
100
Choose all of the lines that have a slope of 5/2.
A, because 10/4 and 5/2 are the same.
E, because if you go up 5 and right 2, the line crosses an intersection every time.
100
The angles of two triangles have been given. Are these two triangles similar? Yes, No, or Not enough Infomation.
Yes, you only need to know 2 angles of a triangle to say they are similar.
100
A process that produces scaled copies is called a ____________.
Dilation
200
Fill in the blank boxes with the missing information if the two figures are congruent.
Show on your board like this:
Top Right:
Bottom Right:
Side Left:
Top Right: 4.5cm
Bottom Right: 6cm
Side Left: 2.8cm
200
Draw and label the triangle after a dilation with a scale factor of 2.
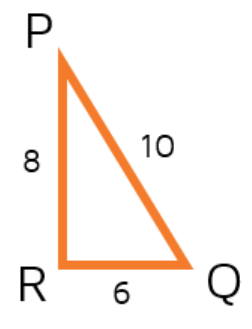
16, 20, and 12
200
Find the slope of the line and explain how you got that.
C. 1.25
Because the rise/run is 2.5/2
200
Similar, because the missing angle for Triangle C would have to be 53o because we know the three angles of a triangle add to 180o.
200
The new image after a dilation is called a _______________.
Scaled Copy
300
These two triangles are similar. Find side lengths a and b.
a = 3
b = 6
300
What would the length of side AC be after a dilation with a scale factor of 1/4?
3
300
Find the slope of the line.
8/4 or 2/1 or just 2
300
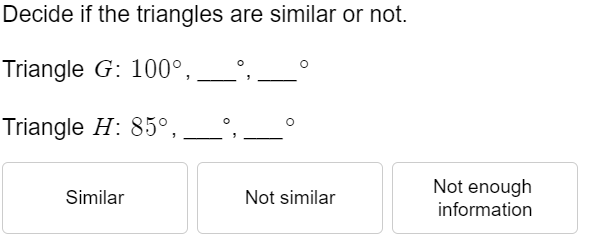
Not enough information.
300
The number you multiply by to create the new image in a dilation process.
Scale factor
400
If the two triangles are similar figures, find the value of x.
x = 5
400
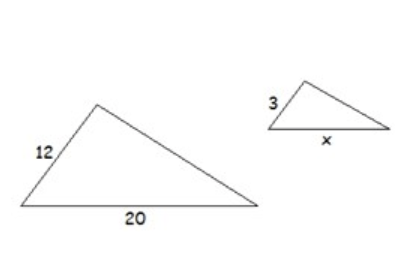
Find the value of x. Hint: remember to divide corresponding sides.
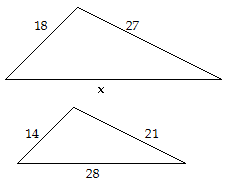
36
400
Find the values of a and b.
a = 5
b = 6
400
Are these two triangles similar? Explain how you know.
No they are not, because there is no scale factor that would multiply 3 to 6, 4 to 7, and 5 to 8.
400
When two figures have the same angles and shape but the side lengths have dilated bigger or smaller they are called _____________________.
Similar figures
500
Triangles ABC and DEF are similar. Find the lengths for segments DF and EF.
EF = 4.47
DF= 5.97
500
Describe how you would dilate this by a scale factor of 1/2 using point A as the center?
You would make each points distance from A, half as long as it used to be.
500
What is the slope of the line?
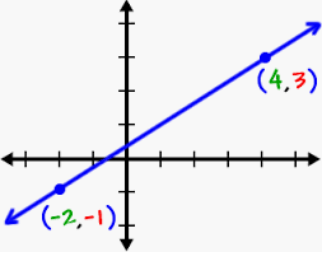
4/6 or 2/3
500
Find the missing side length if the two triangles are similar.
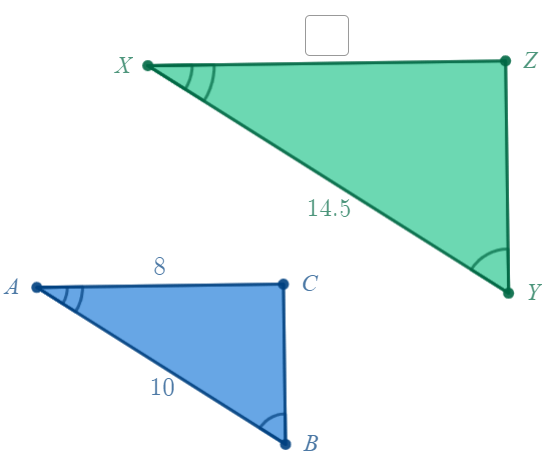
11.6
500
The "steepness" of a line by comparing its rise to its run.
Slope