Extended
Math
11
Logic
Reasoning
100
True of False?
Conclusions based on inductive reasoning will always be true?
What is false?
Inductive reasoning DOES NOT always mean it will be true
100
Deductive reasoning uses ______ to make conclusions?
What are facts, laws, theories?
100
What are the two types of logical reasoning
What is inductive and deductive reasoning
100
The next term in this sequence
6,7,9,12,___
What is 16?
100
The definition of counterexample
What is an example that does not follow an idea or theory?
200
What kind of logic reasoning is this statement?
All students go to school. You are a student. Therefore you go to school.
What is deductive reasoning?
200
How many counterexamples do you need to make a conjecture invalid?
What is the number one?
200
What is an example of a counterexample for this statement:
All odd numbers are prime
What is the number 2?
Number 2 is a prime number but not odd.
200
The sum of 2 even integers is always even.
2+2=4
4+20=24
30+2=32
What type of logical reasoning did I use?
What is inductive reasoning?
I used inductive reasoning because I did not prove this for all cases. I looked at the pattern.
200
What conjecture could you make about the product of two odd integers and one even integer?
What is the conjecture the product of two odd integers is always even?
300
What could I use to represent an odd number when using deductive reasoning?
What is 2x+1?
300
What is one method you can use to solve a problem deductively
What are Venn Diagrams, Number Theory or Two Column Proofs?
300
Find a counterexample: The sum of two numbers is always greater than the larger number used
What is -2+ (-3)=-5?
**or another example that works*
300
PROVE that the difference between an odd integer and an even integer is odd.
What is:
Let 2x=even integer
Let 2y+1=odd integer
(2y-1)-(2x)= 2y-2x-1
2(y+x)+1
Any number doubled plus 1 will be an odd number
300
Write an expression for a three digit number.
What is 100a+10b+c?
400
Select a number. Add 50 to the number. Multiply the sum by 2. Subtract the original number from the product. Solve inductively
What is the result?
What is the result is always 100 more than the selected number?
400
Daisy noticed a pattern when dividing these numbers by 4. The numbers are 33,73,113. Determine the pattern and make a conjecture.
What the cube of an odd number that is one less of a multiple of 4 is divided by 4, the decimal part will result in .75?
400
What are the missing numbers? 
What are the numbers: 20, 27,23?
400
Find a counterexample for this statement:
All furniture that have 4 legs are tables.
What is a chair?
400
Julie made 3 types of holiday treats for all of her holiday company. She made gingerbread, sugar cookies and peanut butter balls. She made 50 of each type. What conjecture can you make about Julie?
What is Julie's conjecture is that her company will eat and like each type of holiday treat equally?
500
What is 14?
(5+3) *3=24
(4+2)*5=30
(1+2)=42/3
500
Think of any number. Multiply that number by 2, then add 6, and divide the result by 2. Next subtract the original number.
What is the result?
What is the number 3?
The result will always be 3
500
What number should go in the fourth box?
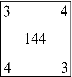
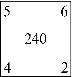
What is the number 30?
500
Use deductive reasoning to prove that the divisibility rule for 3 is valid for a two digit number.
What is...
let ab=two digit number
ab=10a+b
ab=9a+a+b
ab=9a+(a+b)
9a is always divisible by 3 therefore if (a+b) is divisible by three than ab will be divisible by 3.
500
What is the missing number?
What is the number 10?
A,B,C
to find pentagon B: A+C
B-A=C