Unit 1
Unit 2
Unit 3
Unit 4
Unit 5
100
What are 2 ways you could name the plane?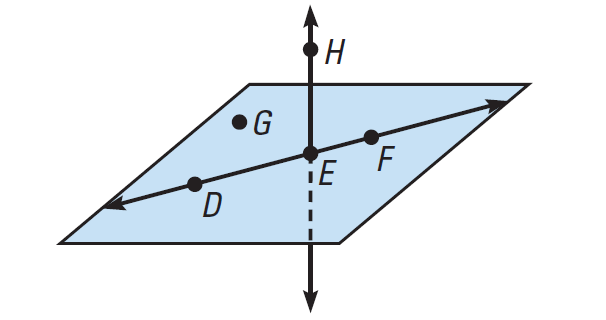
Possible answers: GDE, GEF, GDF, FEG.
100
The next figure in the pattern is A, B, C, or D?
B
100
Assuming lines k and i are parallel. Name a pair of alternate exterior angles.
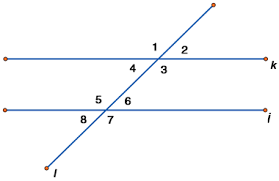
1 and 7
8 and 2
100
Which triangles are isosceles?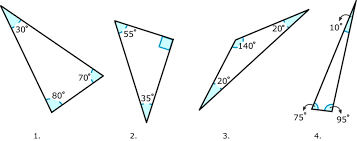
Triangle 3
100
If you wanted to construct the circumcenter of a triangle what lines would you construct to find the point of concurrency?
You would construct the 3 perpendicular bisectors of a triangle.
200
Name one of the lines visible in the figure.
Possible Answers, DE, EF, DF, HE with double arrow over the top.
200
Is the conjecture true or false?
An even number plus 3 is always odd.
If true provide two examples, if false, provide one counter example.
True.
Example: 4+3=7 and 10+3=13
200
Assuming lines k and i are parallel, name a pair of corresponding angles.
1 and 5
2 and 6
4 and 8
3 and 7
200
Which triangles are acute triangles?
Triangle 1
200
If you wanted to construct the incenter of a triangle what lines would you construct to find the point of concurrency?
You would construct the three angle bisectors of a triangle.
300
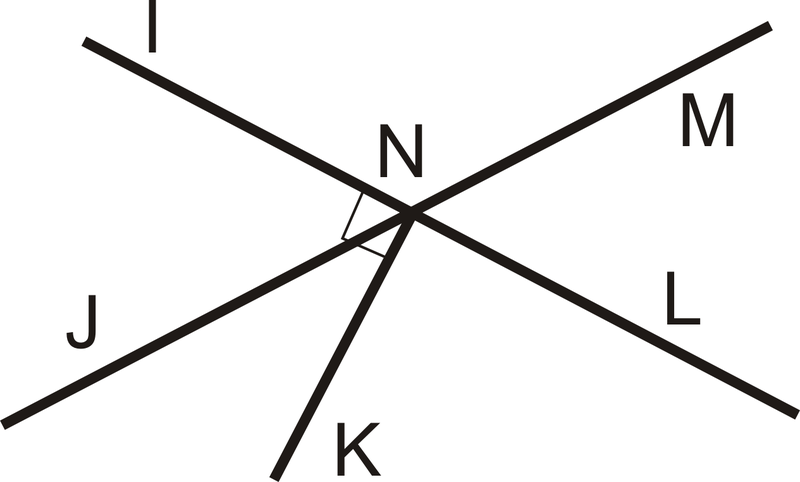
Name a linear pair of angles.
Possible answers:
Angle INM and Angle MNL.
Angle INJ and Angle JNL.
300
Determine if the conditional statement is true or false. If false provide a counter example.
"If two angles are acute, then they are complementary."
False. Angle 1 = 30 and Angle 2 = 40. Both are acute but they are not complementary.
300
Assuming lines k and i are parallel, name a pair of alternate interior angles.
4 and 6
3 and 5
300
Which triangles are scalene?
1, 2, and 4.
300
If you wanted to construct the centroid of a triangle what lines would you construct to find the point of concurrency?
You would construct the 3 medians of a triangle.
400
Name a pair of vertical angles.
Angle INJ and Angle MNL.
400
Determine if the conditional statement is true or false. If false provide a counter example.
"If and angle is acute, then its measure is less than 90°."
True.
400
These pairs of angles are congruent when formed by a transversal through parallel lines.
Corresponding, Alternate Interior, and Alternate Exterior.
400
Which postulate proves these two triangles are congruent?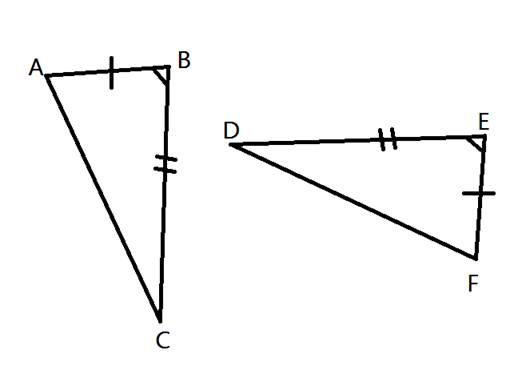
SAS
400
If you wanted to construct the orthocenter of a triangle what lines would you construct to find the point of concurrency?
You would construct the 3 altitudes of a triangle.
500
Name a pair of complementary angles.
Angle INJ and Angle JNK
500
Determine if the conditional statement is true or false. If false provide a counter example.
"If two angles are supplementary, then at least one of them has a measure of 90°."
False. One doesn't have to be 90° for example, 120° and 60°."
500
These pairs of angles are supplementary when formed by a transversal through parallel lines.
Same-side interior angles.
500
What postulate proves these triangles are congruent?
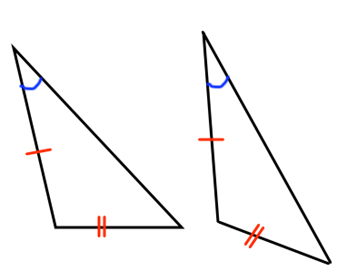
Not enough information to tell if they are congruent.
500
Name the special properties of the circumcenter, incenter, and centroid.
Circumcenter is equidistant from the vertices.
Incenter is equidistant from the sides.
Centroid is the center of gravity or balance point.