Systems
Function Basics
Domain and Range
Function Transformations
Piecewise Functions
100
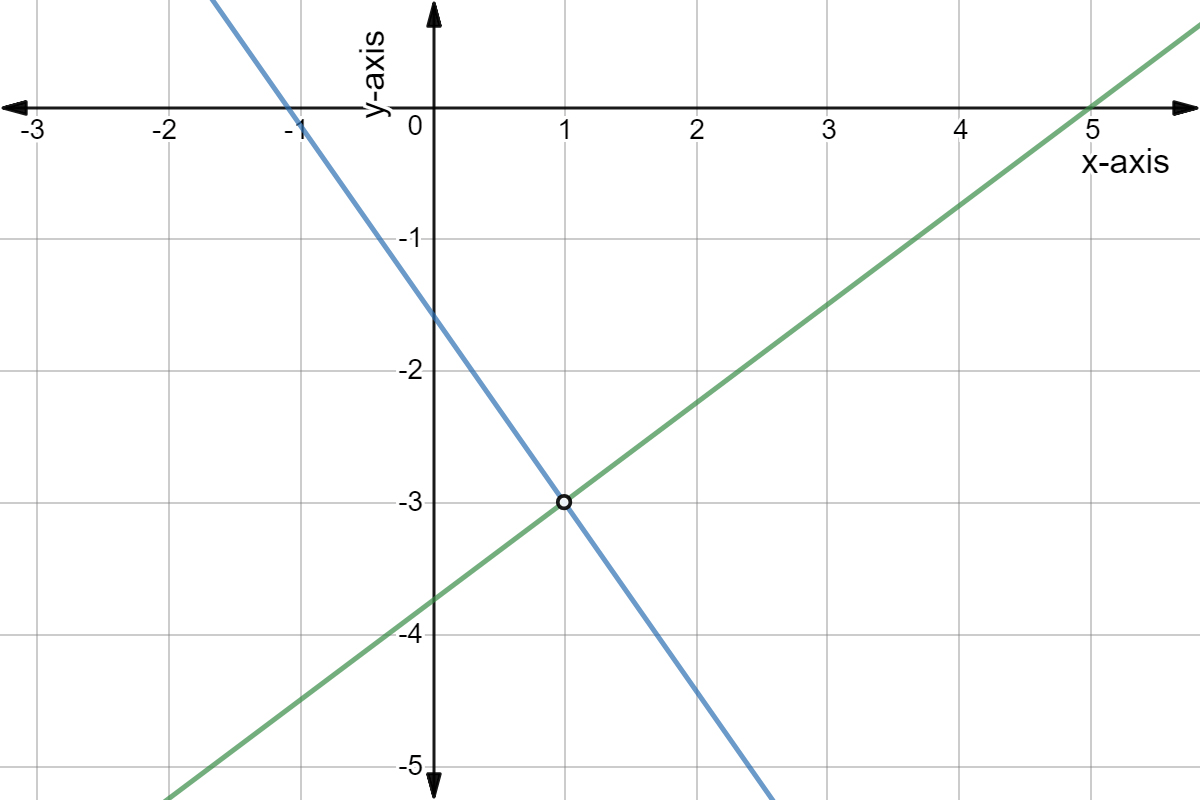
Its the answer to this system
What is (1,-3)
100
This is the interval that this function is increasing on
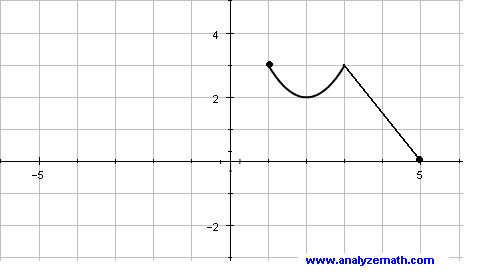
What is (2,3)
100
This is the domain of this function:
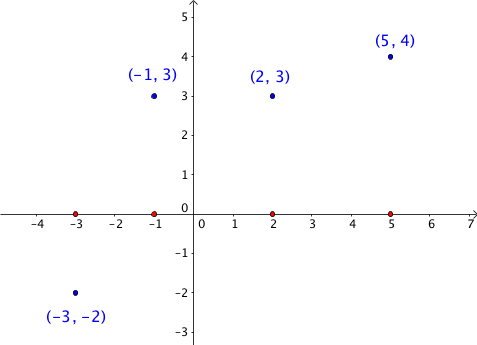
What is (-3,-1,2,5)
100
This is the parent function to
y=(x-4)^2+5
What is
y=x^2
100
This is the domain of this function in interval notation
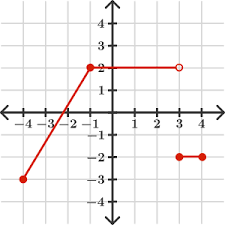
what is [-4,4]
200
It is the answer/answers to this system of equations:
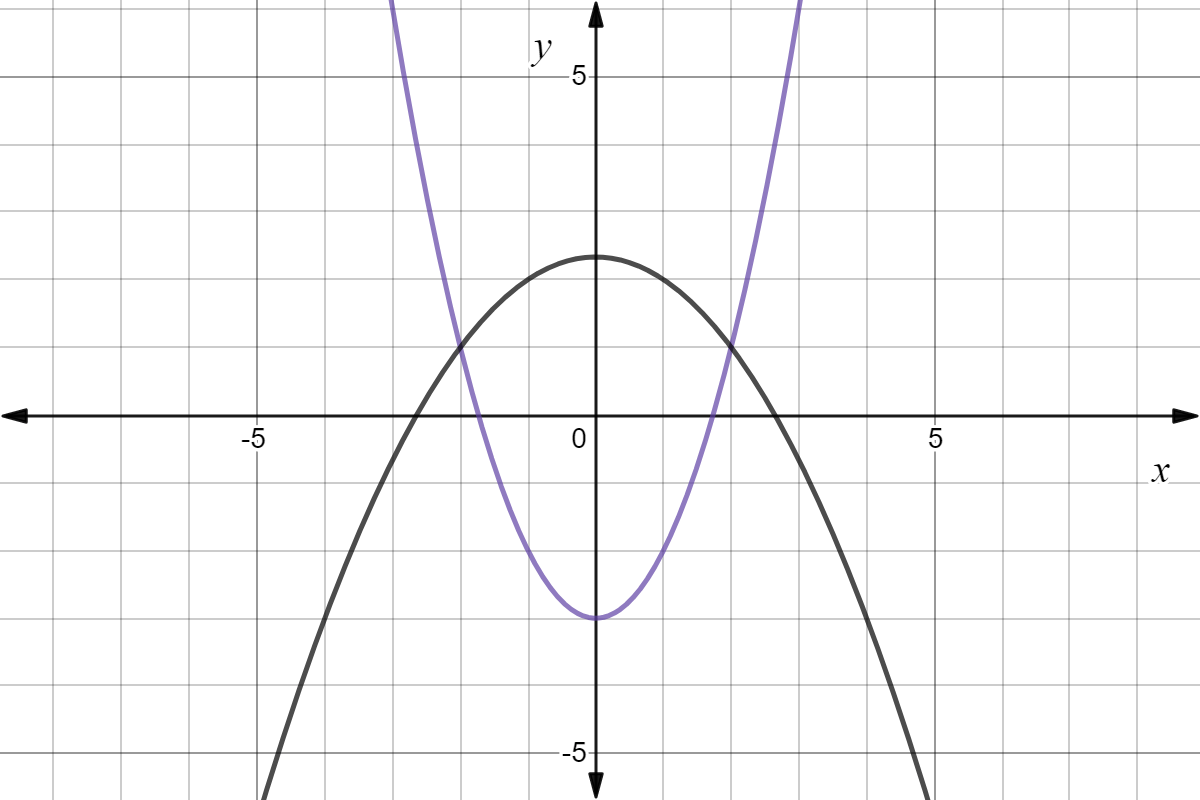
What is (-2,1) and (2,1)
200
These are the zeros of this function:
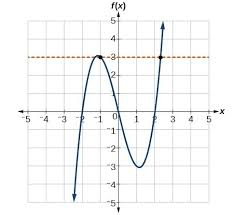
What are (-2,0), (0,0) and (2,0)
200
This is the range of this function:
What is [-5,2]
200
This is the transformation done here:
y=|x-4| +7
What is to the right 4, up 7
200
This is the range of the function in interval notation
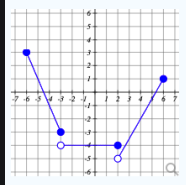
what is (-5,3]
300
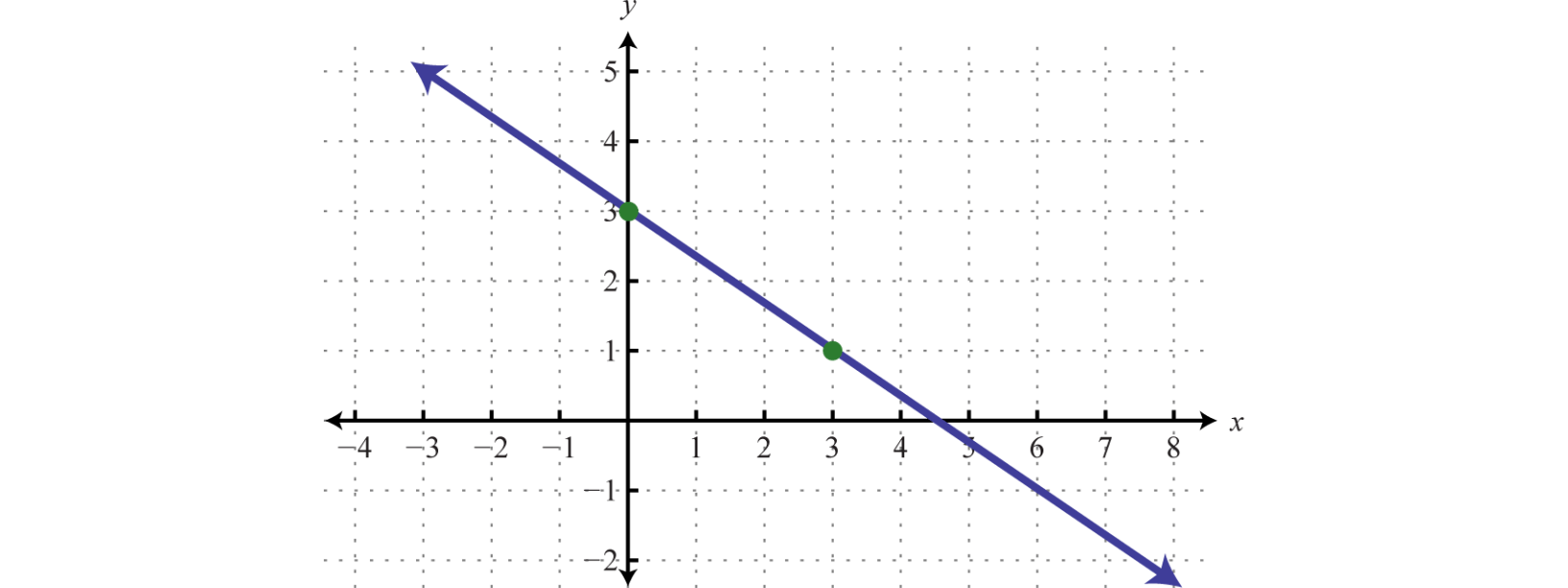
It is the intersection of these 2 lines:
y= -1/3 x -3 and y=2x+4
What is (-3,-2)
300
This is the interval this function is decreasing:
What is ( - infinity, infinity)
300
This is the domain of
x^2
What is (- infinity, infinity)
300
You would graph this transformation by doing this
y=4x^2
What is multiply all the y values by 4
300
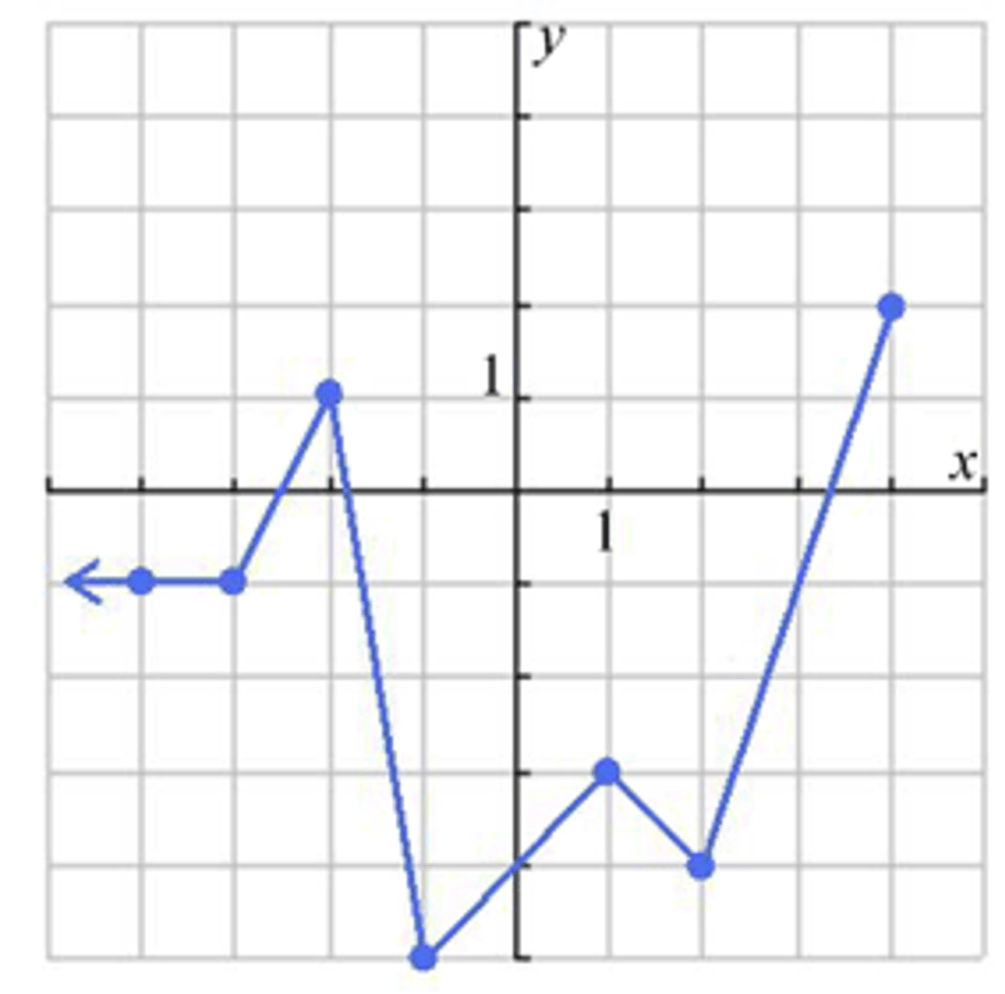
This is the number of equations that represent this piecewise function
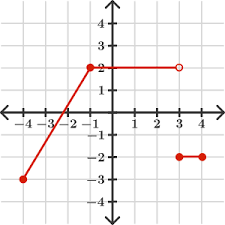
what is 3
400
It is the solution to this system of equations:
-7x-5y=13 and 14x-4y=30
What is (1,-4)
400
This function is positive over this intervals/ intervals:
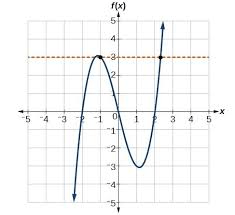
What is (-2,0) in union with (1,infinity)
400
This is the range of
y=|x|+5
What is [5, infinity)
400
The equation of this transformation is....
what is
y=|x+1|+2
400
This are the equations that represents this piecewise function
what is
f(x)= { -1/2 x -1 for (-infinity, -2)
x for [-2,1]
500
Where these 2 lines intersect?
8x-10y=-28 AND -4x+5y=13
What is nowhere, or no solutions
500
This is the interval that this function is decreasing on:
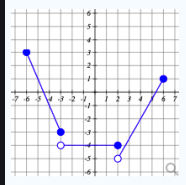
What is [-6,-3]
500
This is the domain of
y=(x+3)^2 -1
What is (-infinity, infinity)
500
The equation for this transformation is...
what is
y=-|x-1|+3
500
This are the equations that represents this piecewise function
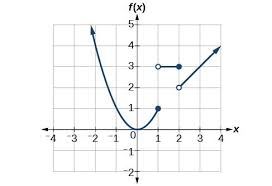
what is
f(x)= { x^2 for (-infinity, 1]
3 for (1,2]
x for (2,infinity)