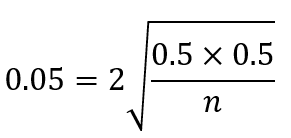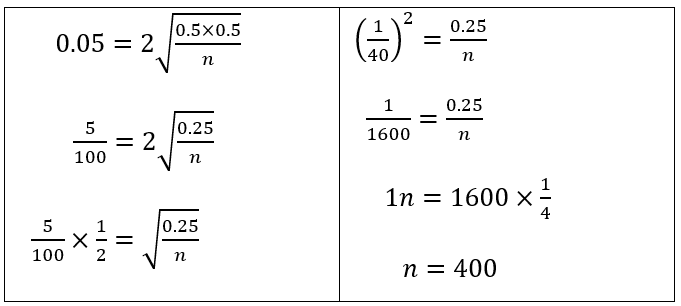No
1^3 -4(1)^2 -5(1)+3ne0
Differentiate
f(x) = 1/x^3
f(x) = x^-3
f'(x) = -3x^-4
=-3/x^4
What is the vertical and horizontal shift of:
y=3cos(2x+pi)-2
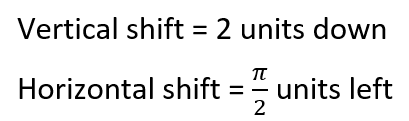
Solve for x:
loge (x) + loge (3) = loge (6)
x=2
Tech Active
Solve to 1 decimal place:
20=90(0.85^x)
x = 9.3
The graph of a cubic has a stationary point of inflection (3, -16), and an x-intercept at (5, 0).
Find the equation.
y=2(x-3)^3-16
Simplify using log laws and differentiate with respect to x
y = ln sqrt(4x-3)
y = ln(4x - 3)^(1/2)
= 1/2 ln(4x - 3)
y'=1/2 xx 4/(4x - 3)
y'= 2/(4x-3)
What is the exact value of:
sin ((7pi)/6)
-1/2
A population of organisms is growing by the formula: N = Number of Organisms t = time in days
Determine the number of organisms after 25 days.
N=3xx2^(0.2t)
96 organisms
Tech Free
2/9-:3/4-1/3
-1/27
Apply the discriminant to
12x^2 -3x + 1
to determine the number of roots.
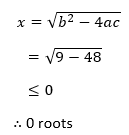
a = 12 b = -3 c = 1
Calculate the gradient of the tangent to the curve at x = -1.
f(x) = x^2 -5x + 1
f'(x) = 2x - 5
f'(-1) = -2 - 5
= -7
Solve
4costheta+1=3
0lethetale2pi
(pi/3,(5pi)/3)
Find the x-intercept of: y = loge (x-2)
(3, 0)
Tech Active
Solve to 1 decimal place within the specified domain:
1/5 sin(x+pi)=1/10
0<=theta<=2pi
x=3.7 and x=5.8
The product of two consecutive odd numbers is 99. Set up an equation and solve it to find one of the numbers.
x=-11 or x=9
Use derivatives to determine the nature of the stationary point at
x=1
of f(x)=x^3 - 3x
f''(1)=6>0
:. Minimum Stationary point
Determine the equation of the tangent to the curve y = 8cos(x) at the point where:
x=pi/2
y=-8x+4pi
Solve for x, showing all answers:
loge (2x) + loge (x + 2) = loge (6)
x = -3 and x = 1
Tech Free Solve for n: