Factoring & Identifying Polynomials
Graphing Polynomials
Finding Inverse Functions
Solving Systems of Equations
Theorems
100
What is the formula for squares of a difference?
What is (x-y)2=x2-2xy+y2
100
Find the zeros of the polynomial.
What is -3, -1, 3?
100
Find the inverse of this original relation.
(0,2)(1,5)(5,6)(8,9)
What is (2,0)(5,1)(6,5)(9,8)?
100
Find the solutions on the graph.
What is (0,-3)?
100
Find the remainder. Use The remainder theorem
6x2-53x-63/ x-10
What is a remainder 7
200
What is the formula for squares of a sum?
What is (x-y)2=x2+2xy+y2
200
Find the end behavior of the polynomial.
What is f(x)→−∞ x→−∞ and f(x)→+∞ x→+∞?
200
Find the inverse function of f(x).
f(x)=2x
What is f^-1(x)=x/2
200
What are solutions?
What is the points on the coordinate plane where the graph of the two equations intersect?
200
Find the roots. Use the Rational Roots Theorem
2x6+8x2-9
What is 1,3,9 and 1/2, 3/2, 9/2
300
Use factor theorem to factor.
f(x)=6x3+3x2+24x+12
What is -1/2 and 2i
300
Find the domain of the polynomial.
What is (-∞,+∞)?
300
Find the inverse of f(x).
f(x)=x-4/2
What is f^-1(x)=2x+4?
300
How many solutions will these equations have.
y=x^3-x^2-x+1
y=x+1
What is 3 solutions?
300
Analyze the roots of the function. Use The fundamental Theorem of Algebra
2x2-2x+1
What is 2 or 0 Roots
400
Use factor theorem to factor.
g(x)= 5x4-35x3-45x2+315x
What is 0,7, and 3
400
Find the range of the polynomial.
What is (-∞,+∞)?
400
Find the inverse of f(x).
f(x)=10-x/5
What is f^-1(x)=5x-10?
400
What are the solutions of these equations?
y=x^4-3x^2-4
y=10x+20
What is (-2,0) and (3,50)?
400
Write a polynomial functions of least degree that has rational coefficients, that has a leading coefficient of 1 and that has the roots -3 with a multiplicity of 2 and -5?
What is x3+11x2+39x+45
500
Use factor theorem to factor.
f(x)=2x5+4x4+5x+10
What is -2 and square root 5/2i
500
Find the zeros, end behavior, domain and range of the polynomial.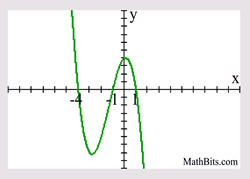 
What is-4,-1,1/f(x)→+∞ x→−∞ and f(x)→−∞x→+∞/(-∞,+∞)/(-∞,+∞)?
500
Are these two functions inverse of each other?
f(x)=3x+15
g(x)=-15+x/3
What is yes?
500
What are the solutions of these equations?
5x=2-y
-10x=-4+2y
What is infinite many solutions?
500
What does the remainder theorem state?
What is that when a polynomial f(x) is divided by a binomial (x-a), the remainder is the value of f(a).