![]() What type of symmetry does this shape have?
What type of symmetry does this shape have?
Line symmetry

Find x and the length of BC
Part + Part = Whole
AB + BC = AC
9x+7 + -3x+20 = 39
x = 2
BC = 14
Given △ABC with m∠A = 45, m∠B = 85, find m∠C.
m∠C = 50
What is the sum of the exterior angles of an octagon?
360o.
The sum of the exterior angles for any polygon is 360o.
p: I did not bring in a key-lime pie.
q: I passed Geometry class.
Give the original conditional statement in the form:
p-->q
as well as the inverse, converse, and contrapositive.
Conditional: If I did not bring in a key-lime pie, then I passed Geometry class.
Inverse: If I did bring in a key-lime pie, then I did not pass Geometry class.
Converse: If I passed Geometry class, then I did not bring in a key-lime pie.
Contrapositive: If I did not pass Geometry class, then I did bring in a key-lime pie.
This image has what type of symmetry?

Point Symmetry

Find x and find m∠ABD
The angles are a linear pair:
Part + Part = Whole
5x+10 + 2x-5 = 180
x = 25
m∠ABC = 135
Which of the following sets of numbers CAN represent the sides of a triangle?
a) 2,4,8
b) 8,8,5
c) 8,10,2
d) 6,9,15
b) 8,8,5
What is the measure of one external angle of a regular 36-gon?
The sum of the exterior angles for any polygon is 360.
360/36 = 10.
One angle measures 10o.
Give the meaning of each logic symbol:
~
∧
∨
→
~ "not" (oppostive/inverse)
∧ "and"
∨ "or"
→ "if/then"
Find the distance between (3,5) and (9,13).
Distance = 10 units.
The point M is the midpoint of segment AB.
Point B has coordinates (-10,6).
Point M has coordinates (-6,8).
What are the coordinates of point A?
A = (-2,10)
Which congruence method proves these two triangles are congruent?
SAS
The angles formed at the intersection C are vertical and thus are congruent.
What is the sum of the interior angles for a 20-gon?
3240o
You can draw 18 triangles inside a 20-gon and each triangle's angles sum to 180o.
Find the radius of a circle whose area is 113.04.
Use the equation A = 𝜋r2.
r = 6
What is the slope of the line that passes through the points (5,8) and (-1,-1)?
9/6
OR
3/2
OR
1.5
Build and equation and find x.
The angles are congruent.
17x - 4 = 12 + 15x
x = 8

Find the lengths of BA and BC
BA: use tangent. BA = 8.40
BC: use cosine. BC = 14.65
Given parallelogram ABCD below:

Given AE = 8
Given DB = 12
Find the lengths of:
CE
DE
BE
CE = 8
DE = 6
BE = 6
Given circle A below. EB is a diameter.
What is the measure of Arc ED?
Measure of Arc ED = 38o
What is the equation of the line of reflection of these figures?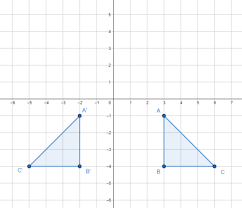
Find the midpoint of A and A': (0.5,-1).
Use the x-value because the line of reflection must be vertical.
x = 0.5
Find x, then find the m∠TRQ.
The angles are congruent because they are vertical.
8x = 2x + 72
x = 12
m∠TRQ = 96o

Given that the two triangles are similar, find x.
Set up a proportion
13/27 = 21/x
Cross-multiply to create an equation
13x = 27*21
x = 43.6
A rectangular park has been built in downtown Richmond. The designer wants to put a gravel walkway diagonally across the park. The width of the park is 80 feet long and the length is 150 feet long. Find the length of the walkway.
The walkway makes the hypotenuse of a right triangle.
The length is 170 feet.

Given circle O with an inscribed decagon.
Find:
m∠AOB
and
m∠OCB
Find the measure of an arc made by one side of the decagon: 360o / 10 = 36o. ∠AOB is twice that.
m∠AOB = 72o
m∠OCB = 36o
By the exterior angle theorem, ∠OCB+∠OBC = ∠AOB. The triangle OBC is isosceles since its legs are both radii of the same circle. So, ∠OCB = ∠OBC.

