Two limits of a function approach a specific point from either the left or the right.
8
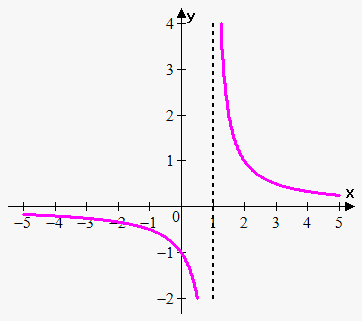
No

Infinite Discontinuity
If f is a continuous function whose domain contains the interval [a, b], then it takes on any given value between f(a) and f(b) at some point within the interval
Intermediate Value Theorem
Find the limit of when x is approaching -1 from the right
-1

Yes
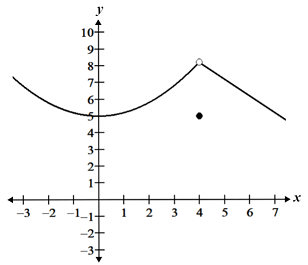
Removable Discontinuity
A theorem which provides a technique to evaluate limits of indeterminate forms.
L'Hopital's Rule
4/5

yes

Jump Discontinuity
A type of discontinuity of functions that occurs at a point where the graph of a function has a hole in it
Removable Discontinuity
8
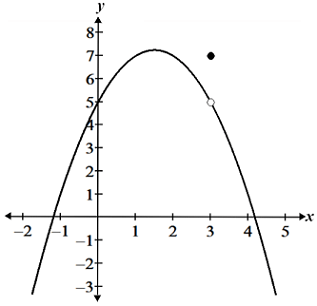
No

Oscillating Discontinuity
A classification of discontinuities in which the function steps from one point to another along the curve of the function, often splitting the curve into two separate section
Jump Discontinuity
Negative Infinity
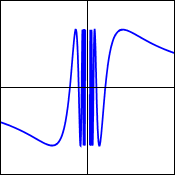
No
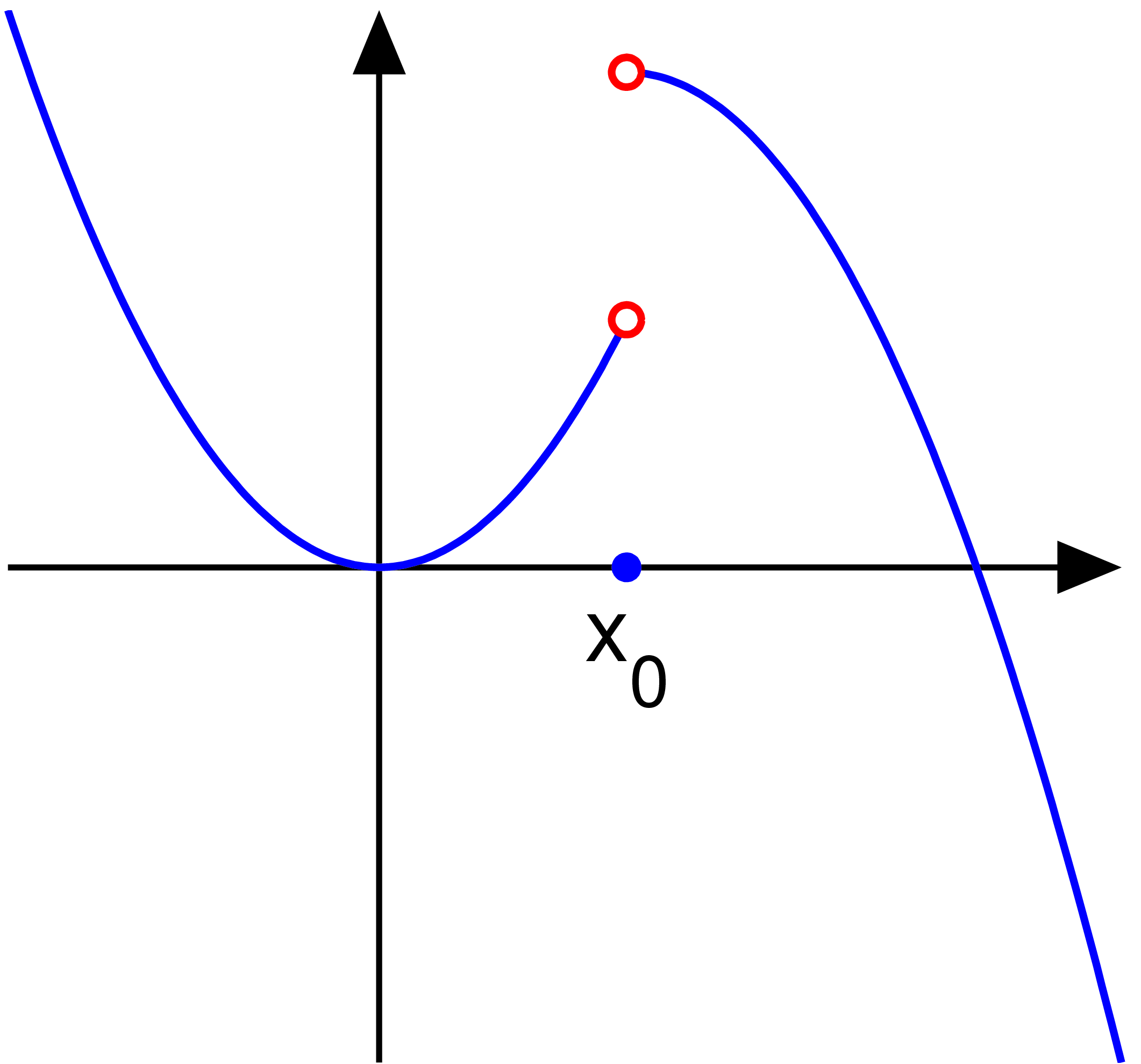
Jump and Removable Discontinuity