Rewrite into fraction form:
root 7 (x^2)
What is x2/7
Solve the quadratic: 2x2 -11x-6=0
What is x = -0.5 and x = 6
Given, ABCD is a parallelogram. If CT = 9, find AT
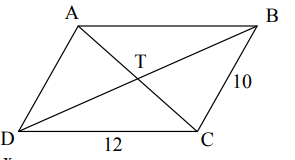
AT = 9
Assume the figure below is a parallelogram, solve for the missing value of x and y. 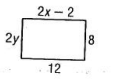
What is y = 4 and x = 7
What is the vertex of the parabola below.
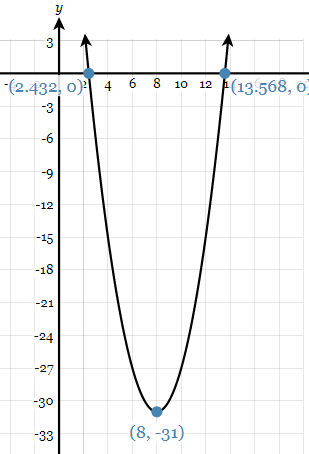
What is (8,-31)
Rewrite in radical form: x4/3
What is
root 3 (x^4)
Solve: 9x2+12x+4=0
What is x = -2/3
Given, ABCD is a parallelograms. If AT = 4x-7 and CT = -x +13, solve for x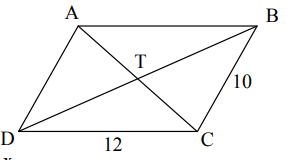
What is x = 4
Given the figure below is a parallelogram, solve for x and y
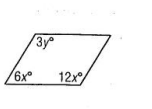
x = 10
y = 40
Find the minimum or maximum of the parabola given below.
y = x2 -12x +29
What is (6,-7)
Simplify the expression as much as possible:
(4x^6)^(1/2)
What is 2x3
Solve (x+1)2 +14=15
What is x = 0 and x = -2
Given PQRS is a rhombus. If m<PMQ = 4x-5, solve for x.
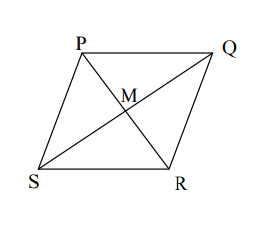
What is x = 23.75
I am a quadrilateral, whose diagonals bisect each other and are perpendicular. What am I?
What is a Rhombus?
Find the minimum or maximum of the parabola given below.
y = x2 +10x+25
What is (-5,0)
Simplify the expression:
(16x)^(5/4)
What is
32xroot4(x)
Solve: x2 -14x-11= -30. Round your answer to the nearest tenth.
What is x = 12.5 and x = 1.5
Given PQRS is a rhombus. If PQ = 3x+7 and QR = -x+17, find the length of PQ
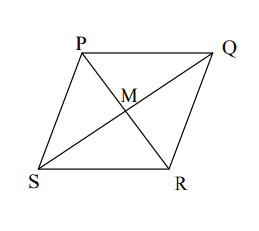
What is 22.
Given the figure below is a parallelogram, solve for x and y.
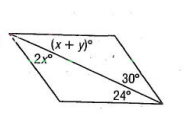
What is x = 15 and y = 9
Find the minimum or maximum of the parabola given below.
y = -x2 +8x+5
What is (4,21)
Simplify the expression below:
1/((8x)^(-2/3)
What is
4x^(2/3)
Solve: 5(x+5)2-33= 2
What is x =
-5 + root 2 (7)
-5 - root 2 (7)
Given that ABCD is a parallelogram, find the perimeter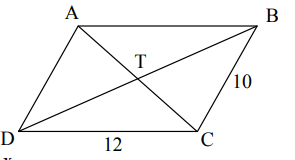
What is 44
Given CDEF is a rhombus and that EC = 10 and GC = -4x+9. Solve for x.
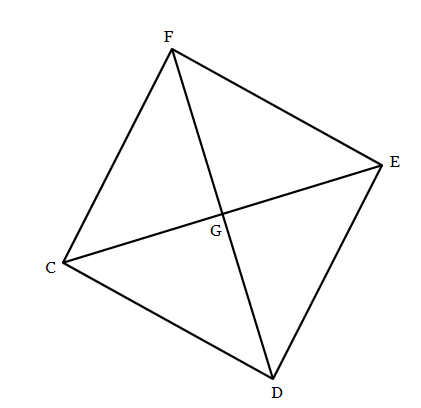
x = 1
Find the minimum or maximum of the parabola given below.
y = -3x2 -42x-159
What is (-7,-12)