Vocabulary
Operating w/ Rational #s
Reasoning Algebraically
Thinking Proportionally
Other
100
______________ represents the distance from zero on a number line, always resulting in a positive value.
Absolute value
100
Determine the sign of the product or quotient.
The product of two numbers with opposite signs
negative
100
Evaluate the algebraic expression for x = (− 4)
− 5x
20
100
Write the fractional rate as a unit rate.
1/2 cup for 3 batches
1/6 cup per batch
100
2/7 + 4/6
40/42 or 20/21
200
A _____________ is a number or an algebraic expression that is a factor of two or more numbers or algebraic expressions.
common factor
200
Determine the sum.
45 + (−27)=
18
200
5m(2n – 7)
10mn – 35m
200
Write the fractional rate as a unit rate.
6 pages every 1/5 hour
30 pages an hour 1/30 hour per page
200
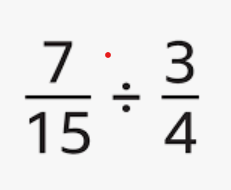
28/45
300
The _______________ describes how the dependent variable changes for every unit that the independent variable changes.
unit rate of change
300
Determine the difference.
−20 − (−30) =
10
300
Solve the equation 5c + 2 = 27
c=5
300
Solve each problem by setting up and solving a proportion.
The 18 wind turbines on Windy Hill are enough to meet the electrical needs of all 6 houses on Breezy Lane. How many wind turbines are needed to meet the electrical needs of 26 houses?
78 wind turbines
300
2.7 x 5.8
15.66
400
A _____________ is a ratio in which one or both of the quantities are fractions. When comparing complex ratios, rewrite them as unit rates.
complex ratio
400
Complete the number sentence with + or –.
2 ___ (− 2) = 0
+
400
Solve –4x + 5 ≥ – 3
x ≤ 2
400
Solve each problem by setting up and solving a proportion.
Between 1990 and 2000, the population of New York City increased at a rate of 32 people every 4 hours. By how many people would the population have increased in 63 hours?
504 people
400
53
Write in expanded form and solve
5 x 5 x 5= 125
500
_______ are operations that “undo” each other.
Inverse operations
500
The temperature in Chattanooga, Tennessee, is −3°C. The temperature in Sam’s hometown is 18 degrees Celsius colder than that. What is the temperature in Sam’s hometown?
(−3) - 18 = −21
The temperature in Sam’s hometown is −21°C.
500
4(x − 9) = − 48
-3
500
Solve each problem by setting up and solving a proportion.
Nicholas owns a pet bearded dragon named Oscar, which is a type of lizard. It typically eats 51 crickets in 2 days. How many days has Nicholas fed Oscar if it has eaten 102 crickets?
4 days
500
Double Jeopardy
2x + 4(3n - 4 + x) - 12n
6x - 16