Is it a Function?
Evaluating Functions
Domain and Range
Increasing/Decreasing
End Behavior
100
Is this a function?
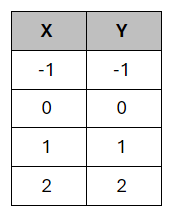
Yes, it is a function because none of the x-values repeat.
100
Evaluate the following function for f(-2)
f(x) = 5x^3+6x^2+4x
f(-2)= - 24
100
What is the domain of the following set of values:
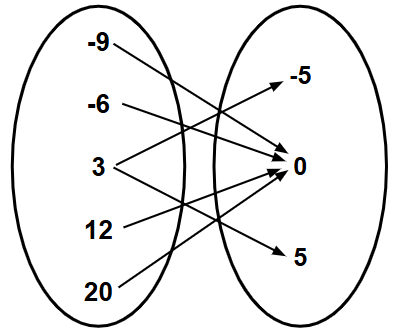
{-9, -6, 3, 12, 20}
100
Identify the vertex of the following function and decide if it is a maximum or minimum:
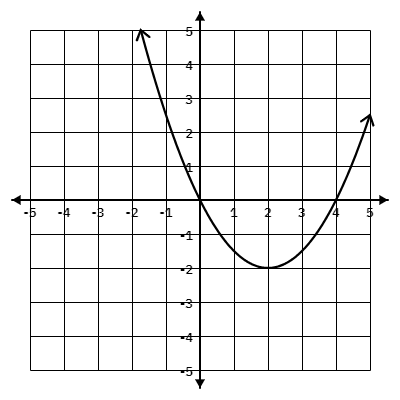
The vertex is at (2,-2) and it is a minimum.
100
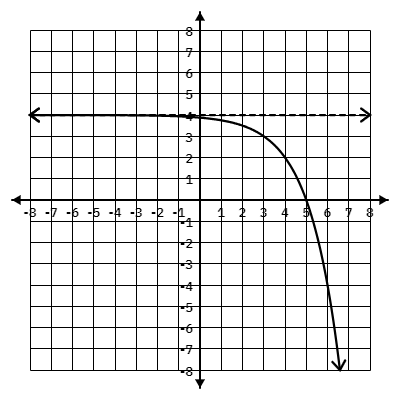
Finish the end behavior for the graph below:
As x -> \infty, y ->
\infty
200
Is this a function?
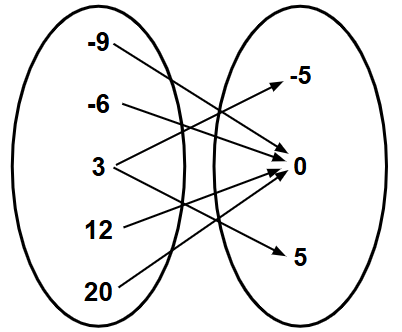
No, it is not a function, the x-value 3 repeats/is used twice.
200
Evaluate the following function for g(-16)
g(x)=x^2/(2x)
g(-16) = -8
200
Identify the range:
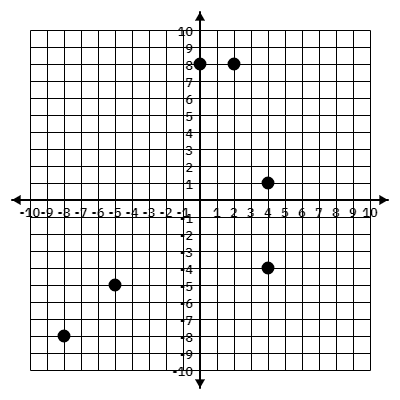
{-8, -5, -4, 1, 8}
200
State the interval of increasing and decreasing for this graph.
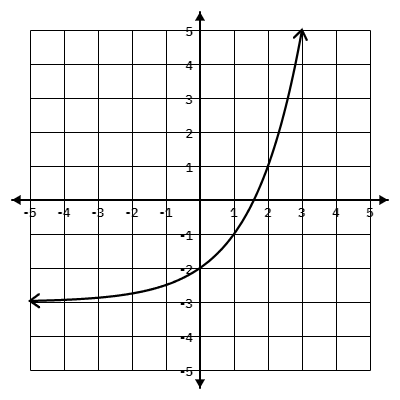
Increasing:
(-oo, oo)
Decreasing: Never
200
Write the end behavior for the graph below:
300
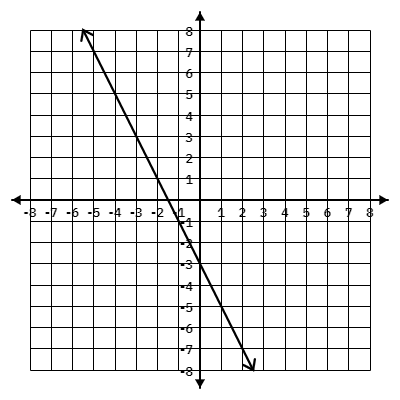
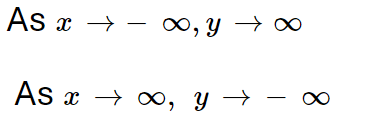
Which two points make this relation not a function?
(4,1) and (4, -4)
300
if f(x) =-6 , find x
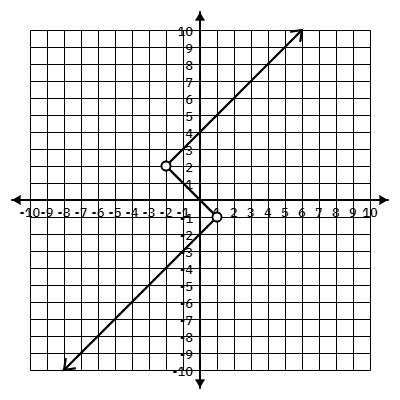
x= -4
300
Write the range for the following graph:
Range: [-4, 8]
300
At what interval is this graph increasing?
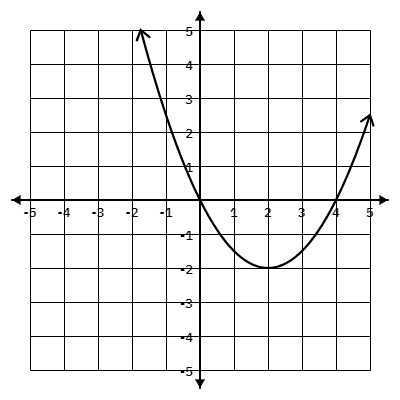
(2, \infty)
300
Finish the end behavior for the graph below:
As x -> - \infty, y -> __
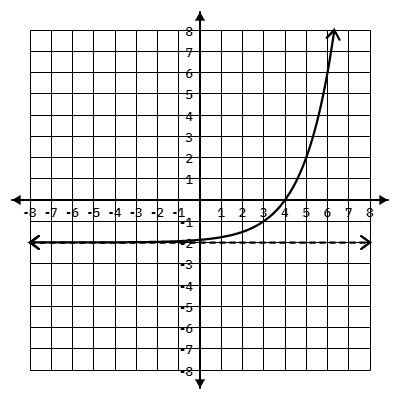
As x -> - \infty, y -> -2
400
Analyze the relation below:
{(-1,3) (0,3) (4,2) (7,12) (12,7)}
Is it a function? Explain your answer.
Yes, it is a function because none of the x-values are repeated.
400
Find f(-2)
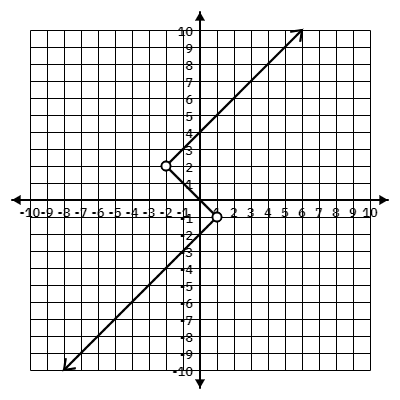
if f(-2) = -4
400
Write the domain and range of the following graph:
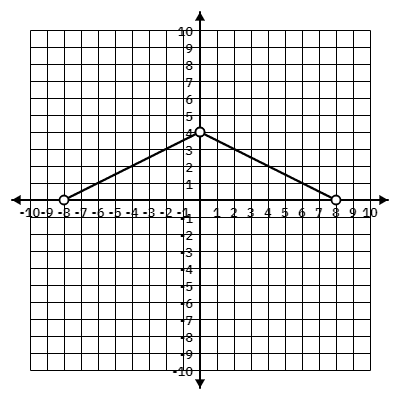
Domain: (-8,8)
Range: (0,4)
400
Identify all intervals at which the following graph is decreasing:
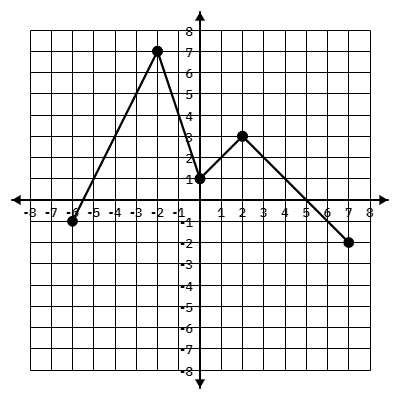
The graph is decreasing (-2,0) and (2,7)
400
Choose all of the graphs with
the following end behavior:
as x-> -\infty, y -> infty
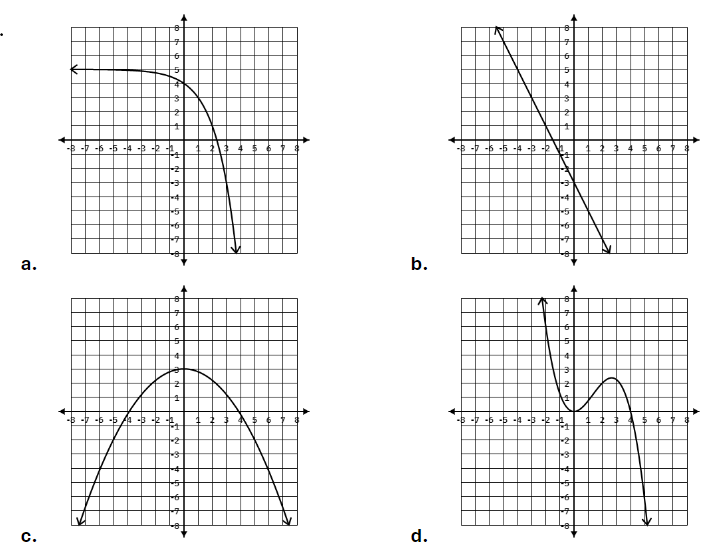
B and D
500
Is this graph a function? Explain.
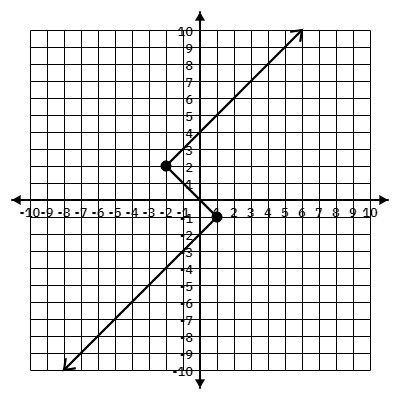
This graph is not a function because:
- it does not pass the vertical line test
- there is more than 1 point on some x-values
- x-values are repeated.
500
Find f(1)
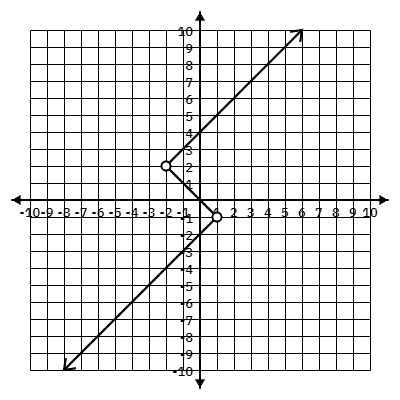
f(1) = 5
500
Write the domain and range of the following graph:
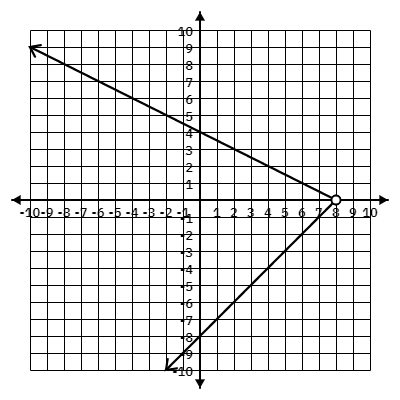
Domain:
(-oo, 8)
Range:
(-oo, oo)
500
Identify all graphs that are decreasing from (-\infty, \infty)
a and b
500
Write the end behavior for the graph below:
