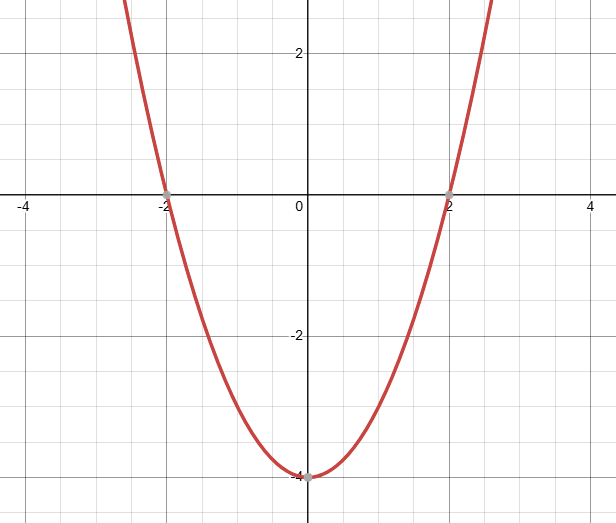
Describe the transformation applied to the graph of
y=x^2 - 4
Vertical translation 4 units down.
Determine the vertex form equation for the equation given below:
y=x^2+8x+16
y=(x+4)^2
Expand the following expression:
(x-1)(x-1)
x^2-2x+1
Given the vertex form equation below, a student said the transformations being applied to get the graph of the equation below are:
- horizontal translation 2 units to the left;
- vertical translation 7 units up.
What is the error?
y=(x-2)^2+7
2 units to the right, not left
Describe the transformations applied to the graph of y = x^2 to obtain the graph of the equation below.
y=(x-5)^2+5
Horizontal translation 5 units to the right, and vertical translation 5 units up.
Find the missing number (BLANK) below that makes the equation a perfect square trinomial:
y=x^2-10x+(BLANK)
25
Determine the standard form equation for the equation given below:
y=(x+7)^2-37
y=x^2+14x+12
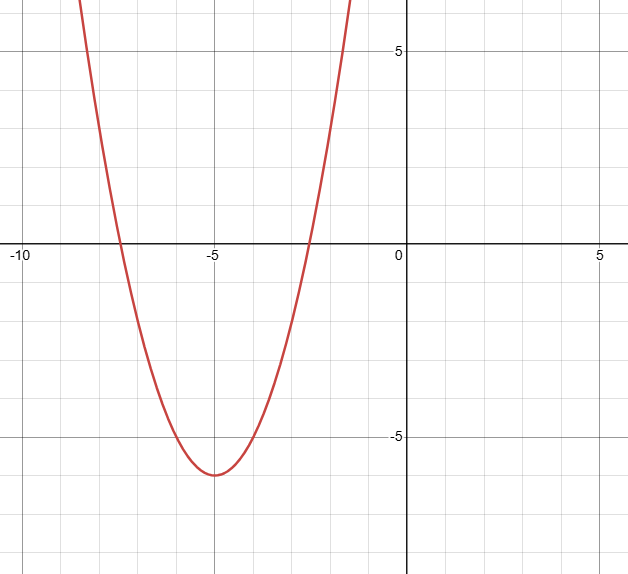
A student wrote the vertex form equation for the graph above. Determine why it is wrong.
y=(x-5)^2-6
Since the graph has moved 5 units to the left, it should be (x + 5) in the brackets, not (x - 5).
Given that a = -3, determine the vertex form equation where the vertex is V(-2, 38).
y=-3(x+2)^2+38
Determine the vertex for the equation given below:
y=x^2-8x+21
(4, 5)
Expand and simplify the equation below:
y=3(x-2)^2-5
y=3x^2-12x+7
Identify the error in the steps below:
y=2(x-1)^2-6
y=2(x^2-2x+1)-6
y=2x^2-4x+1-6
y=2x^2-4x+5
Third line, forgot to multiply the 1 by 2. And fourth line, 1 - 6 = -5, not +5.
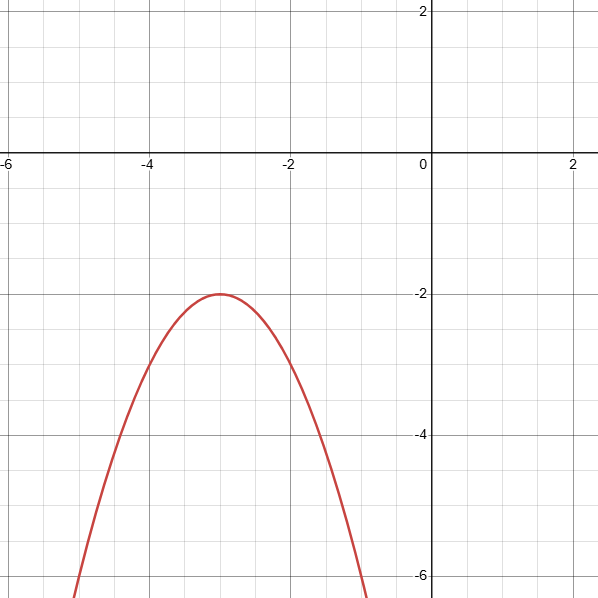
Describe the transformations applied to the graph of y = x^2 to obtain the given graph above.
Reflection about the x-axis, horizontal translation 3 units to the left, and vertical translation 2 units down.
Find the missing number (BLANK) below that makes the equation a perfect square trinomial:
y=x^2+(BLANK)x+100
20
Determine the standard form equation for the equation given below:
y=-1/2(x+7)^2+2
y=-1/2x^2-7x-22.5
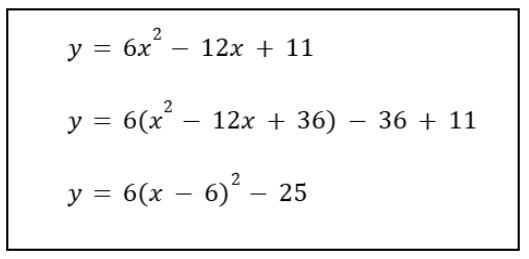
Spot the mistake in the problem above, and describe how to fix the issue.
In the second line, when "adding zero", the -36 is not being multiplied by 6.
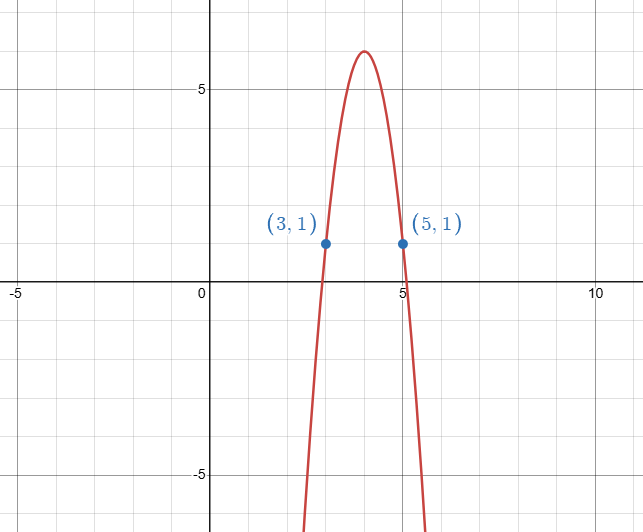
Describe the transformations applied to the graph of y = x^2 to obtain the graph given above.
Reflection about the x-axis, vertical stretch by a factor of 5, horizontal translation 4 units to the right, and vertical translation 6 units up.
Determine the vertex form equation for the equation given below:
y=-4x^2+32x-67
y=-4(x-4)^2-3
Determine the standard form equation for a parabola that has a vertex of V(6, 11) and that passes through the point P(12, -7).
y=-1/2x^2+6x-7
An equation was given to be y = -2(x + 4)^2 + 8.
A student wrote that the transformations are:
- Reflection
- Vertical compression by a factor of 2
- Horizontal translation 4 units to the right
- Vertical stretch by 8
Determine the errors, and fix the issues.
"Reflection about the x-axis, vertical stretch by a factor of 2 (not compression), horizontal translation 4 units to the left (not right), and a vertical translation (not stretch) 8 units up."