Quadratic Formula
Part 1: f(x)=-2x^2+4x+6
Part 2: f(x)=-2x^2+4x+6
Part 1: f(x)=x^2+6x+9
Part 2: f(x)=x^2+6x+9
100
Find the discriminant, number of solutions, and type of solution(s):
f(x)=8x^2+6x-5
b^2-4ac
(6)^2-4(8)(-5)
Discriminant: 196
Number of Solutions: 2
Type of Solutions: Real
(Since the discriminant is positive, there are 2 real solutions)
100
Find the discriminant:
f(x)=-2x^2+4x+6
b^2-4ac
(4)^2-4(-2)(6)
64
100
What is the direction of opening for this quadratic?
f(x)=-2x^2+4x+6
a=-2
Since a is negative, the direction of the opening is:
Down
100
Find the discriminant:
f(x)=x^2+6x+9
b^2-4ac
(6)^2-4(1)(9)
0
100
What is the direction of opening for this quadratic?
f(x)=x^2+6x+9
a=1
Since a is positive, the direction of the opening is:
Up
200
Find the discriminant, number of solutions, and the type of solutions:
f(x)=4x^2-2x+7
b^2-4ac
(-2)^2-4(4)(7)
Discriminant: -108
Number of Solutions: 2
Type of Solutions: Non-real
(Since the discriminant is negative, there are 2 non-real solutions)
200
What is the y-intercept for the following quadratic?
f(x)= -2x^2+4x+6
x=0 for the y-intercept. Plug in 0 for x:
-2(0)^2+4(0)+6
0+0+6
(Plugging in zero cancels the first 2 terms. Which means y=c)
(0,6)
200
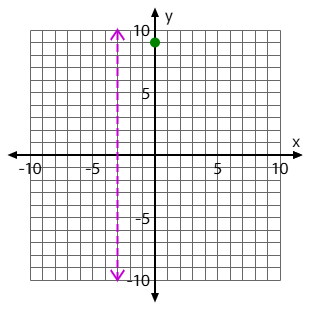
Graph the y-intercept for this quadratic:
f(x)= -2x^2+4x+6
Use your paper to graph. The green dot is the ordered pair for the y-intercept. It should look like this:
200
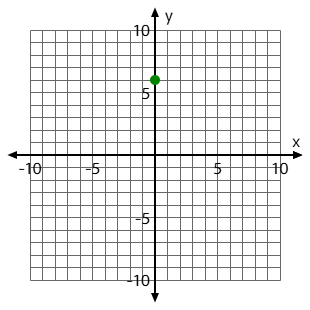
What is the y-intercept for the following quadratic?
f(x)= x^2+6x+9
x=0 for the y-intercept. Plug in 0 for x:
(0)^2+6(0)+9
0+0+9
(Plugging in zero cancels the first 2 terms. Which means y=c)
(0,9)
200
Graph the y-intercept for this quadratic:
f(x)=x^2+6x+9
Use your paper to graph. The green dot is the ordered pair for the y-intercept. It should look like this:
300
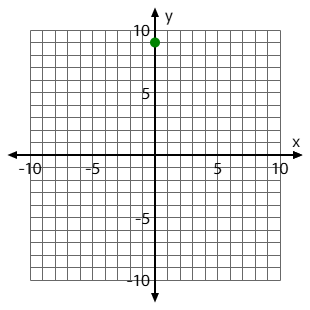
Use the quadratic formula to solve for x:
2x^2+4x+2=0
b^2-4ac
(4)^2-4(2)(2)
Discriminant: 0
frac{-bpmsqrt(b^2-4ac)}{2(a)}
frac{-(4)pmsqrt0}{2(2)}
frac{-4}{4}
x=-1
300
Find the Axis of Symmetry for this quadratic:
f(x)= -2x^2+4x+6
frac{-b}{2a}
frac{-(4)}{2(-2)}
frac{-4}{-4}
x=1
300
Graph the Axis of Symmetry of this quadratic:
f(x)= -2x^2+4x+6
Use your paper to graph. The pink dotted line is the Axis of Symmetry. It should look like this:
300
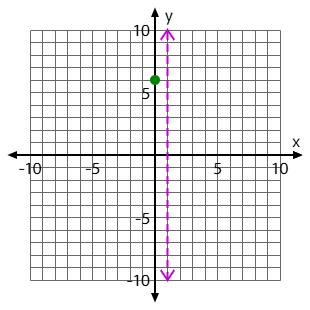
Find the Axis of Symmetry for this quadratic:
f(x)=x^2+6x+9
frac{-b}{2a}
frac{-(6)}{2(1)}
frac{-6}{2}
x=-3
300
Graph the Axis of Symmetry of this quadratic:
f(x)=x^2+6x+9
Use your paper to graph. The pink dotted line is the Axis of Symmetry. It should look like this:
400
Use the quadratic formula to solve for x:
0= -2x^2+4x+6
b^2-4ac
(4)^2-4(-2)(6)
Discriminant: 64
frac{-bpmsqrt(b^2-4ac)}{2(a)}
frac{-(4)pmsqrt64}{2(-2)}
frac{-4+8}{-4}
x=-1
frac{-4-8}{-4}
x=3
x=-1, 3
400
Find the ordered pair of the Vertex:
f(x)= -2x^2+4x+6
Use the axis of symmetry x-value (x=1) to find the ordered pair of the Vertex:
y=-2(1)^2+4(1)+6
y=8
(1,8)
400
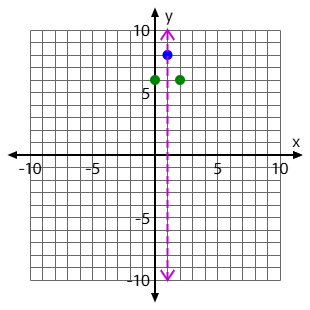
Graph the Vertex for this quadratic:
f(x)= -2x^2+4x+6
Use your paper to graph. The blue dot is the ordered pair for the vertex. It should look like this:
400
Find the ordered pair of the Vertex:
f(x)=x^2+6x+9
Use the axis of symmetry x-value (x=1) to find the ordered pair of the Vertex:
y=(-3)^2+6(-3)+9
y=0
(-3,0)
400
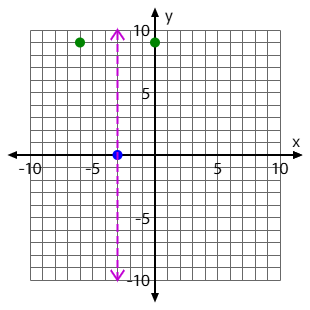
Graph the Vertex for this quadratic:
f(x)=x^2+6x+9
Use your paper to graph. The blue dot is the ordered pair for the vertex. It should look like this:
500
Use the quadratic formula to solve for x:
-17x^2-7x+2=3
-17x^2-7x-1=0
b^2-4ac
(-7)^2-4(-17)(-1)
Discriminant: -19
x=frac{-bpmsqrt(b^2-4ac)}{2(a)}
x=frac{-(-7)pmsqrt(-19)}{2(-17)}
x=frac{7pmisqrt19}{-34}
500
(Use the quadratic formula or solve by factoring. Use the discriminant from the previous question.)
Find the x-intercepts:
f(x)= -2x^2+4x+6
x=frac{-bpmsqrt(b^2-4ac)}{2a}
x=frac{-(4)pmsqrt(64}{2(-2)}
x=frac{-4pm8}{-4}
x=frac{-4+8}{-4}
x=-1
x=frac{-4-8}{-4}
x=3
Since y=0 for x-intercepts, the x-intercepts are:
(-1,0) and (3,0)
500
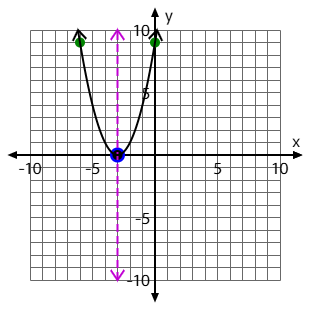
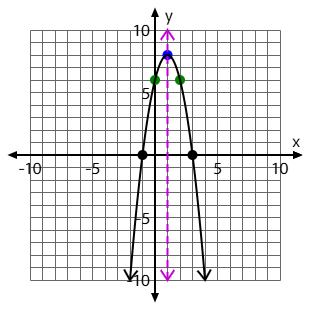
Graph the x-intercept(s) for this quadratic:
f(x)= -2x^2+4x+6
Use your paper to graph. The black dots are the x-intercepts. Your final graph should look like this:
500
(Use the quadratic formula or solve by factoring. Use the discriminant from the previous question.)
Find the x-intercepts:
f(x)=x^2+6x+9
x=frac{-bpmsqrt(b^2-4ac)}{2a}
x=frac{-(6)pmsqrt0}{2(1)}
x=frac{-6pm0}{2}
x=frac{-6}{2}
x=-3
Since y=0 for x-intercepts, the x-intercept is:
(-3,0)
500
Graph the x-intercept(s) for this quadratic:
f(x)=x^2+6x+9
Use your paper to graph. The black dot is the x-intercept, which is also the vertex in this case. Your final graph should look like this:
