Love Triangles
Work Those Quads
Similar, but Not the Same
Face Full of Trigonometry
Circles & Stuff
100
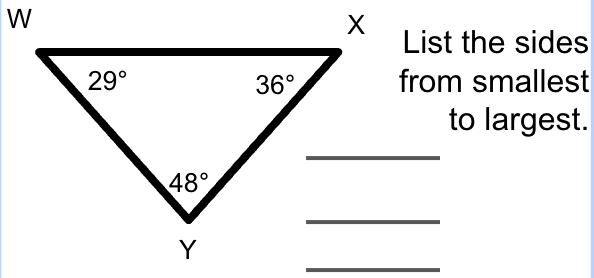
1) XY
2) WY
3) WX
100
Find the value of x.
180(5-2) = 540
(5x+2)+(3x+5)+(8x+8)+(4x+15)+(5x+10) = 540
25x+40 = 540
x=20
100
Find the length of CD
if quad ABCD ~ RSTU.
(y+2)/12 = 5/6
6(y+2)=(12)(5)
y+2=10
y=8
CD=y+2=8+2=10
100
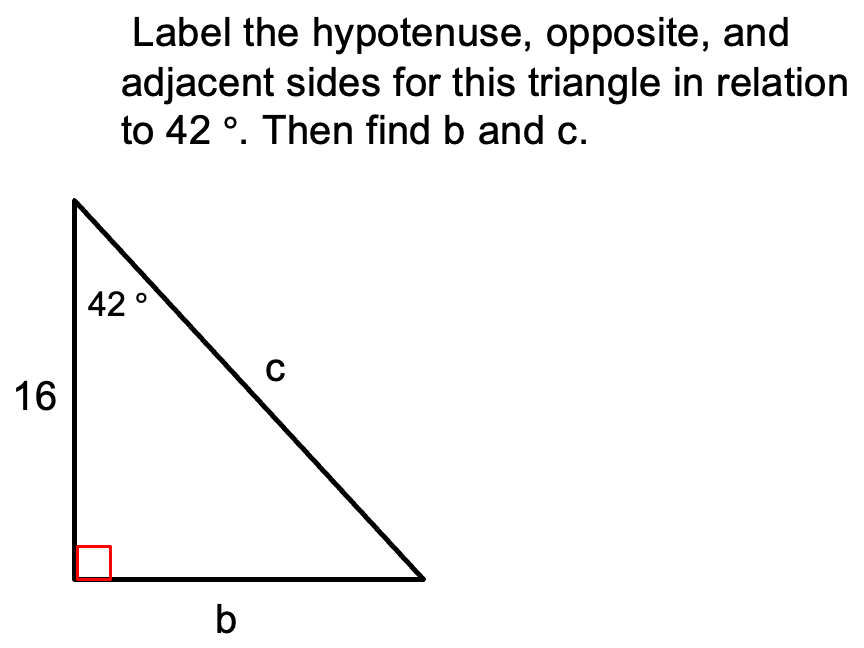
adjacent hypotenuse
opposite
b = 14.4065 c = 21.5301
100
Find the values of x and y.
2y+1=y+4
y=3
5x-18=3x-4
2x=14
x=7
200
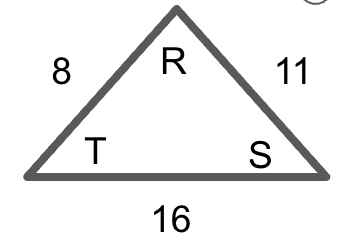
List the angles from smallest to largest.
m∠S, m∠T, m∠R
200
This is a rhombus. Find LO.
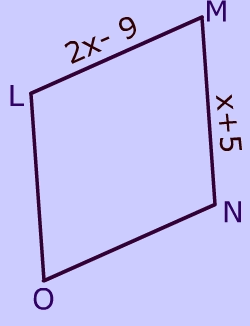
MN cong LO
LM cong MN
2x-9=x+5
x=14
LO = 14+5 = 19
200
The 2 triangles are similar.
What is the length of CD?
(HINT: What theorem will help you
find AB?)
6^2+AB^2=10^2
AB^2=100-36
AB=8
AC/CD = AB/ED
6/CD = 8/12
8(CD) = 72
CD=9
200
What is
theta?
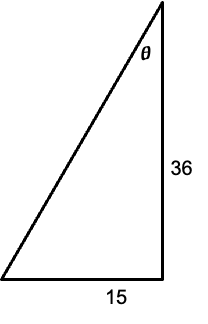
ፀ = 22.6199°
200
What is the arch length of AB if x = 48 degrees and r = 18? (Leave pi in answer.)
24/5 pi
300
What is a segment that divides an angle in half to make 2 congruent angles?
Angle bisector
300
Solve for
angleSPQ
angleSPQ cong angleSRQ
(6z-5)+(2z+25)=180
8z=160
z=20
angleSPQ=2(20)+25=65
300
What kind of triangle does the statement determine?
a2 + b2 < c2
What theorem says this it true?
__________________________________
__________________________________
Obtuse triangle, according to the Pythagorean Inequality Theorem
300
Solve the triangle.
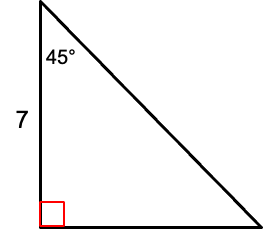
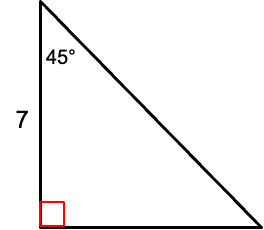
45 degrees
leg = 7
hypotenuse = 7sqrt2
300
What is the arc length of major arc AB if r = 30 and x = 60?
5pi
400
Is it possible to make a triangle with the following sides? Show the statement that proves yes or no.
29 ft, 62 ft, 17ft.
No.
17 + 29 cancel(>) 62
400
Name 3 kinds of parallelograms
ie. rectangle, rhombus, square
400
Write the coordinates of S'V'U'T of a dilation with a scale factor of 4.
S(-2,-2), V(-1,1), U(1,1), T(0,-2)
S'(-8,-8), V'(-4,4), U(4,4), T(0,-8)
400
What is the area of this triangle? (Round to 4 sig figs.)
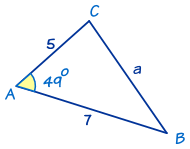
A = (1/2)bc sin A
= (1/2)(5)(7) sin 49
A=13.2074
400
What is the area of the blue sector?
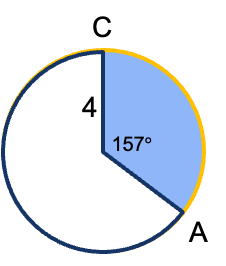
157/360 pir^2
314/45 pi
500
Find the possible values of x.
angleMOP > angleMON
therefore 4x+12 > 5x+3
x < 9
500
Find x.
(1/2)(AC+TI)=VE
(1/2)[(x+6)+(3x-2)]=4x+1
(1/2)(4x+4)=4x+1
2x+2=4x+1
1=2x
x=1/2
500
x/5.9 = 3.1/4.8
4.8x=18.29
x=3.8
500
Solve for the variable. Round to 4 decimal places.
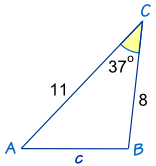
SAS - Law of Cosines
c^2 = a^2 + b^2 - 2ab*cos C
c = 6.6663
500
Solve for x. Round to the nearest tenth.
x2+212=(x+9)2
x2+121=x2+18x+81
40=18x
x=2.2