A triangle named triangle ABC has the following coordinates: A(-4,2) B(-3,3) C(2,1)
What are the new coordinates of the triangle A'B'C' if translated 2 units down?
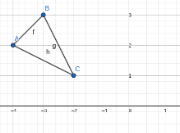
New coordinates of Triangle A’B’C’:
A’ = (-4,0) B’ = (-3,1) C’ = (-2,-1)
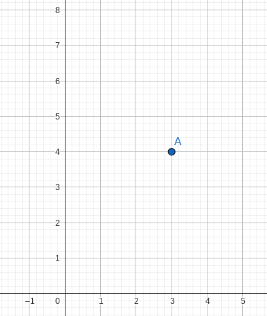
Point A(1,4)
If I reflected point A over the y axis and translated it 1 unit up, what is the coordinate of point A''?
A''( -1, 5)
Does an octagon have rotational symmetry? If so, what is the order?

Yes, 8
What kind of triangle has 3 lines of symmetry?
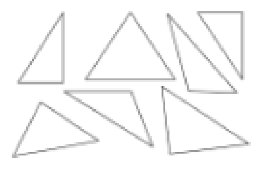
An equilateral triangle has three lines of symmetry.
What is the rule for reflecting across the x axis?
(x, y) -> (x, -y)
Figure ABC has points A(6,5), B(8,2) and C(4,2). Reflect figure ABC across the y axis, Then translate 2 units down. Where will A’B’C’ be?
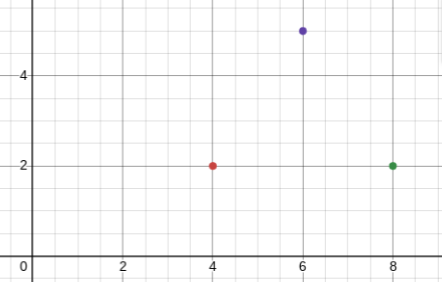
A’(-6,3) B’(-4,0) C’(-8,0)
If I translated the shape 6 units to the left and 7 units up and then rotated 180 degrees. Fill in the rules
(x,y) —> (x- __ , y + __ ) —> (__,___)
(x,y) ---> (x-6, y+7) -----> (-x,-y)
What is the order of Rotational Symmetry of a star?

The answer is 5
Is a parallelogram symmetrical? Why or why not?
How can you find the number of lines of symmetry in a regular hexagon?
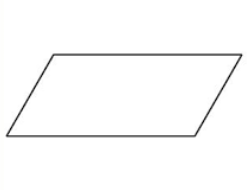
A parallelogram is NOT symmetrical. When folded along the diagonal line it does not result in the same shape in two halves.
What is the rule for rotating 180 degrees?
(x, y) -> (-x, -y)
Figure ABCD has points A(0,6), B(3,3), C(6,6) and D(3,0). Translate figure ABCD 3 units down and 2 units to the left, Then reflect A’B’C’D’ across the y-axis. What are the points?
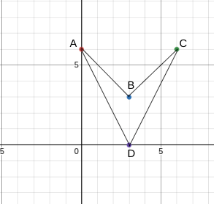
A''(2,3) B''(-1,0), C''(-4,3) D''(-1,-3)
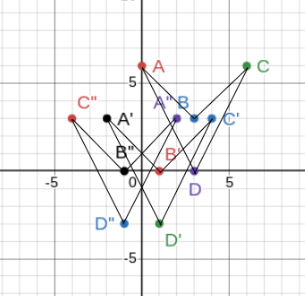
Point A(1,4), point B(5,6) point C(3,2)
If these points are translated 2 units to the right and 4 units down, then reflected over the line y= x, what are the coordinates of the points.
A''(0,3) B''(2,7) C''(-2,5)
If this shape has rotational symmetry, how many degrees will it have to rotate to complete a single turn?
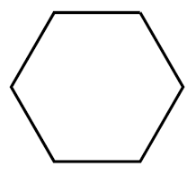
It will have to rotate 60 degrees.
How many sides does a Hendecagon have? How many lines of symmetry does a Hendecagon have?
It has 11 lines of symmetry. It has 11 sides.
What is the rule for reflecting across the y axis and rotating 180 degrees? (non-combined)
(x, y) -> (-x, y) -> (-x, -y)
Trapezoid ABCD has coordinates A(-4,4), B (-2,2), C(-2,-2) and D(-4,-4). Rotate the figure about the origin 450 degrees counterclockwise about the point origin, then translate A’B’C’D’ 8 units to the left and 7 units down. What are the coordinates of A"B"C"D"?
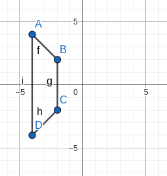
A’’(-12,-11) B’’(-10,-9) C’’(-6,-9) D’’(-4,-11)
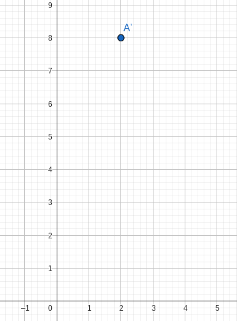
Reflect point A over the _______ axis, rotate ____, translate the figure 5 units up and _______ units to the left. Point A(3,4). Point A'''(2,8)
Reflect point A over the y axis, rotate 90 degrees clockwise, and translate the figure 5 units up and 2 units to the left.
Hi, I'm a regular polygon that has the same number of sides as the number of multiplication tables that a high schooler should have memorized, and my angle of rotation is the same number that Messi wore while playing for PSG. What is my Angle of Rotation?

The answer for this question would be 30, because the multiplication tables you should memorize in High School are the ones from 1-12, which means that the polygon has 12 sides. This means that to get the angle of rotation of the polygon, you should divide 360 by 12 which is 30 degrees. Messi's number wasn't important (:
What shape is it? How many lines of symmetry does it have? What’s its interior angles?
How can you determine the number of lines of symmetry in a regular dodecagon?
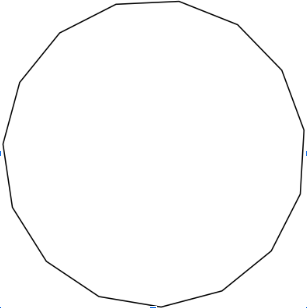
This shape is a Pentadecagon or Pentakaidecagon. It has 15 lines of symmetry. It has interior angles of 156.
First, you must know what a dodecagon is. A dodecagon has 12 sides and 12 angles, and you can figure this out by looking at the first part of the word. The Greek word, “dodeka” means twelve. And then you determine the lines of symmetry.
What is the rule for rotating 90 degrees clockwise around the origin, and reflecting across the x axis?
(Combined - use point (2,3) to test your combination)
(x,y) -> (y, -x) -> (x, -y)
Combined: (x, y) -> (y, x)
A (-3, 3) B (-2, 3) C (-1, 3) D (-3, 0) E (-1, 0)
If you translate ABCDE 8 units to the right, and 6 units down. Then rotate ABCDE by 450 degrees clockwise, then reflect across the x axis. What are the coordinates of A’B’C’D’E’?
A’(-3, 5) B’(-3, 6) C’(-3, 7) D’(-6, 5) E’(-6, 7)
Triangle ABC has the vertex A(3,7) B(4,2) C(1,3). After a sequence of transformations, the triangle has the vertex A””(-5,-2). What are the coordinates of the vertex A”, B”, C”, B”” and C””? What was the sequence of the transformations?
A"(-1,-1) B”(-2,4) C”(-4,2) B””(-6,-7) C””(-8,-5)
Rotate 180 degrees CW around point C. Reflect over line A’B’, Translate 4 units to the left and 3 units up, and reflect over the x-axis.
I am a regular polygon that has the same order as lines of symmetry, and my angle of symmetry is equal to the number of hearts that 13 octopuses and 1 human have. What polygon am I and what is my angle of symmetry?

Nonagon, 40 degrees
What shape is this?
How many lines of symmetry does it have?
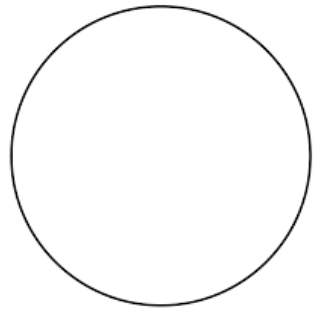
A circle and it has an infinite number of lines of symmetry.
What is the rule for rotating 270 degrees counter clockwise around the origin, translating 3 units up, 2 units left and reflecting over the y axis?
(Combined -- use point (1,3) to check)
(x, y) -> (y, -x) -> (x - 2, y + 3) -> (-x, y)
Combined: (x, y) -> (-y + 2, -x + 3)