What is the equation for calculating the slope from two points?
y2 - y1 / x2 - x1
Graph the equation:
y = 2x - 4
Start at -4. Up 2 to the right 1.
Write the equation of the line in slope - intercept form with a slope of 10 that goes through the point (0, 200).
y = 10x + 200
State whether the lines are parallel, perpendicular, or neither:
y = 5x - 10
-1x + -5y = 3
perpendicular
What is the pythagorean theorem?
a2 + b2 = c2
Calculate the slope of the line that goes through the points: (9, -13) and (8, 5)
-18
What is the correct equation of the line?
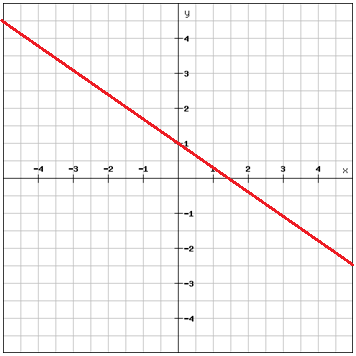
y = -2/3x + 1
Write the equation of the line in any form that goes through the points: (4, -3) and (9, 12).
y - 12 = 3(x - 9) or y = 3x - 15
Write the equation of the line parallel to the line
y=-3x+7 through the point (6, 6).
y-6 = -3(x-6)
y=-3x+24
Find the distance between the two points!
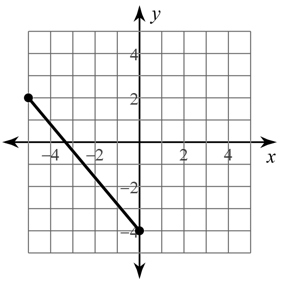
7.81
What is the slope of the line:
9x - 18y = 36
1/2
Graph the equation:
y = -7/5x + 6
Start at 6. Down 7, right 5.
Rewrite the equation in slope intercept form:
-6x + 16y = 48
y=3/8x + 3
Write the equation of the line in slope intercept form perpendicular to the line 3x - 4y = 10 through the point (0, 7).
y=-4/3x+7
Find the distance between the two points!
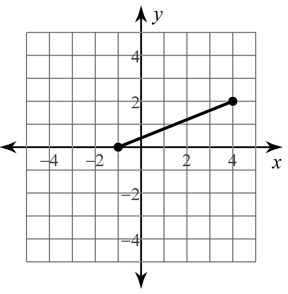
5.39
What is the slope of the line: x = 0?
undefined!
Name the 4 equations of the lines that make up this square:

y = 4.5
y = -4.5
x = -4.5
x = 4.5
Write the equation of the line in slope intercept form with a slope of -4 and an x intercept of 5.
y=-4x+20
Name the vertical line perpendicular to the line y=0 that passes through the origin!
x=0
Find the distance from the Pet Store to the Drug Store. What is this side of the triangle called?
8.06 - the HYPOTENUSE!
Find the value of r if the slope of the line through (5, -11) and (8, r) is -1/3.
-12
Solve this system of equations by graphing:
***Your answer is the ordered pair that the lines intersect at!
2x+y= 15
3x−y= 5
(4, 7)
Write the equation of the line in BOTH slope intercept and point slope form that goes through the points
(-7, 3) and (2, 1)
y - 1= -2/9 (x - 2)
y= -2/9 x + 13/9
Find r so that the lines are parallel.
Line 1: goes through the points: (-1, 8) and (4, -12)
Line 2: goes through the points: (6, r) and (7, 3)
r = 7
Using the DISTANCE FORMULA, find the distance between these two points:
(6, 4) and (-3, -4)
sqrt of 145 (12.04)
