Write the equation in function form/slope-intercept form.
-y=6x
y=-6x
Find the x-intercept of x + 22y = 5 . Write the x-intercept and write it as an ordered pair.
x+22(0)=5
x+0=5
x=5
(5,0)
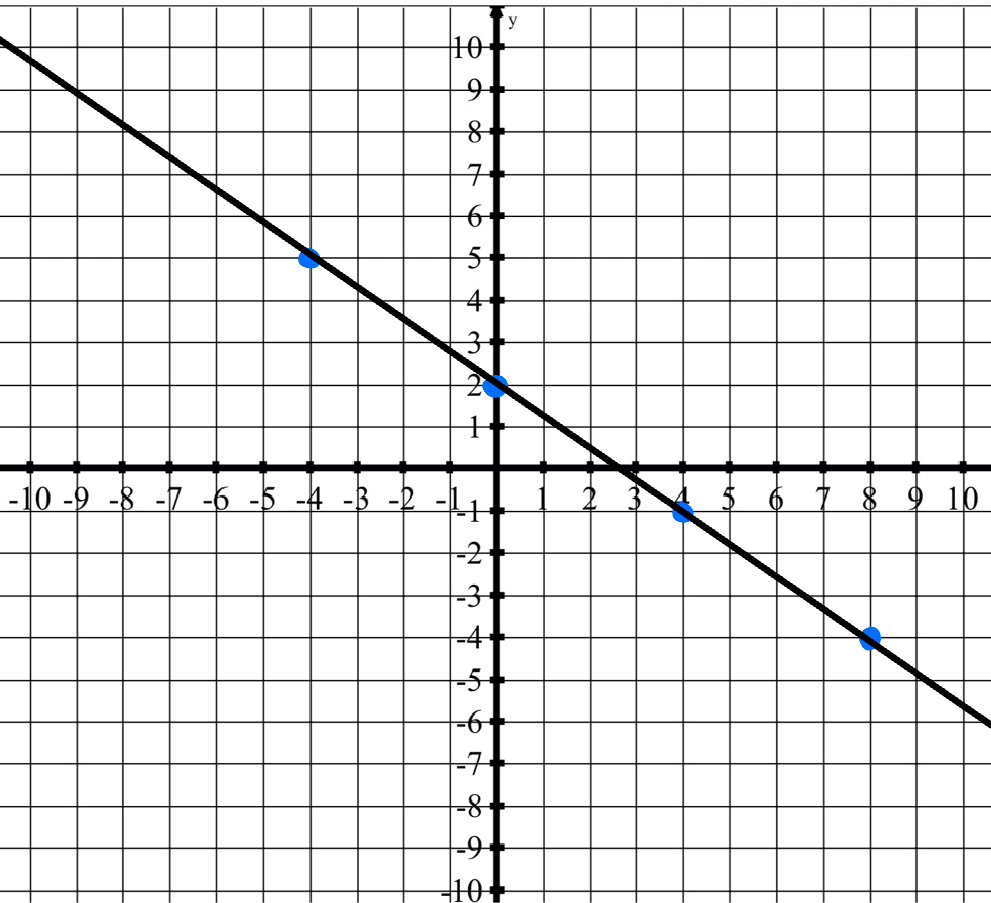
Is this a linear function function? If so, explain why. 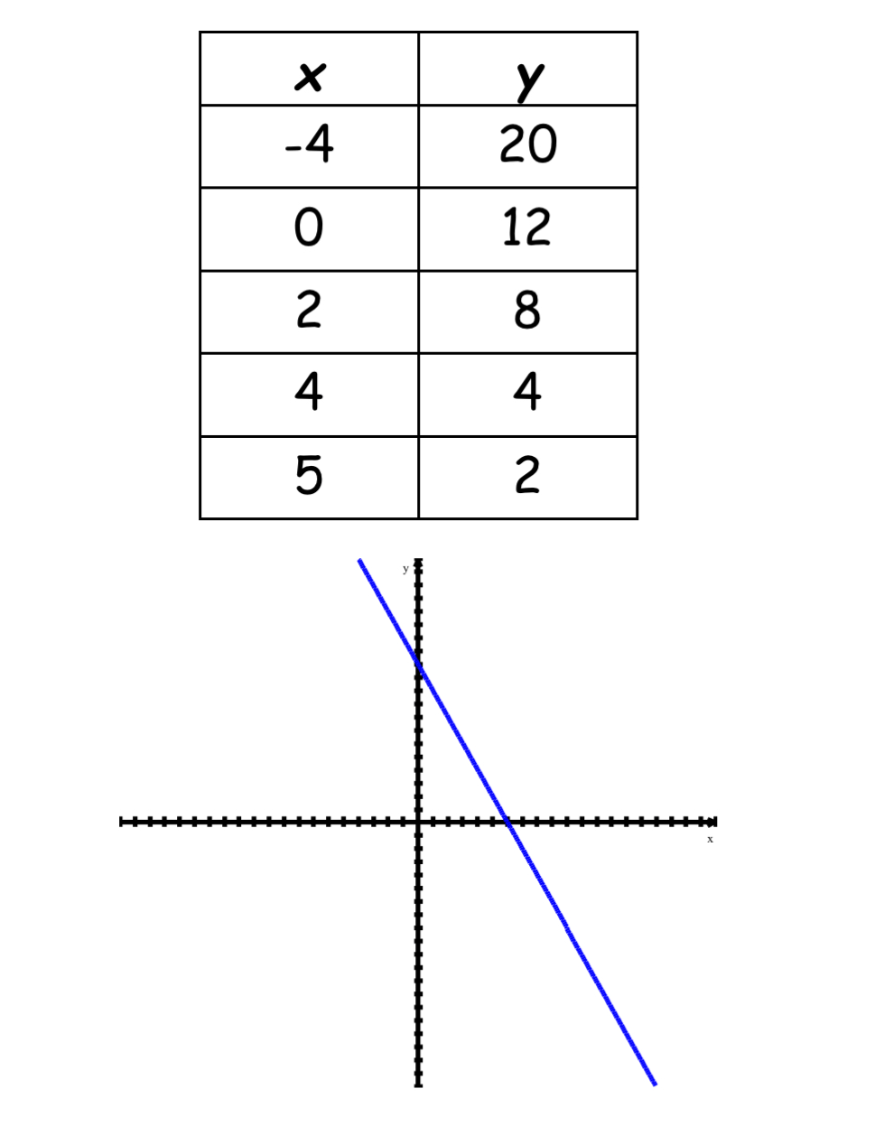
Yes, it is a linear function.
Explanation: The rate of change is constant.
What is the slope of the line
y=-2x+ 8
m=-2
What is the slope of the line:
y=1/2x+8
m=1/2
Write the equation in function form/slope-intercept form.
9x + y = 12
y = - 9x +12
Find the y-intercept of x + 5y = 15 . Write the y-intercept and write it as an ordered pair.
0+5y=15
(5y)/5=15/5
y = 3
(0,3)
Determine whether the table represents a linear or nonlinear funtion. SHOW YOUR WORK. Provide an explanation.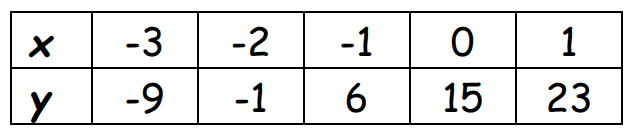
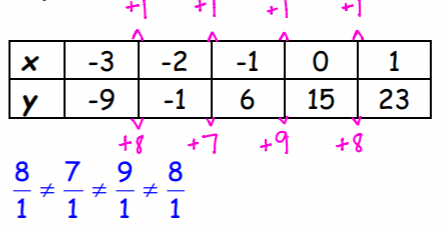
The table represents a nonlinear function. The rate of change is not constant.
Find the slope of the line passing through the following points:
(5, -12) and
(-11, -36)
Note: Write your final answer as an integer, a reduced proper fraction, or a reduced improper fraction.
m=3/2
Identify the slope and y-intercept of the line with the given equation. Use the slope and y-intercept to graph the equation.
y=4x
y-intercept: y=0 (0,0)
slope: m=4
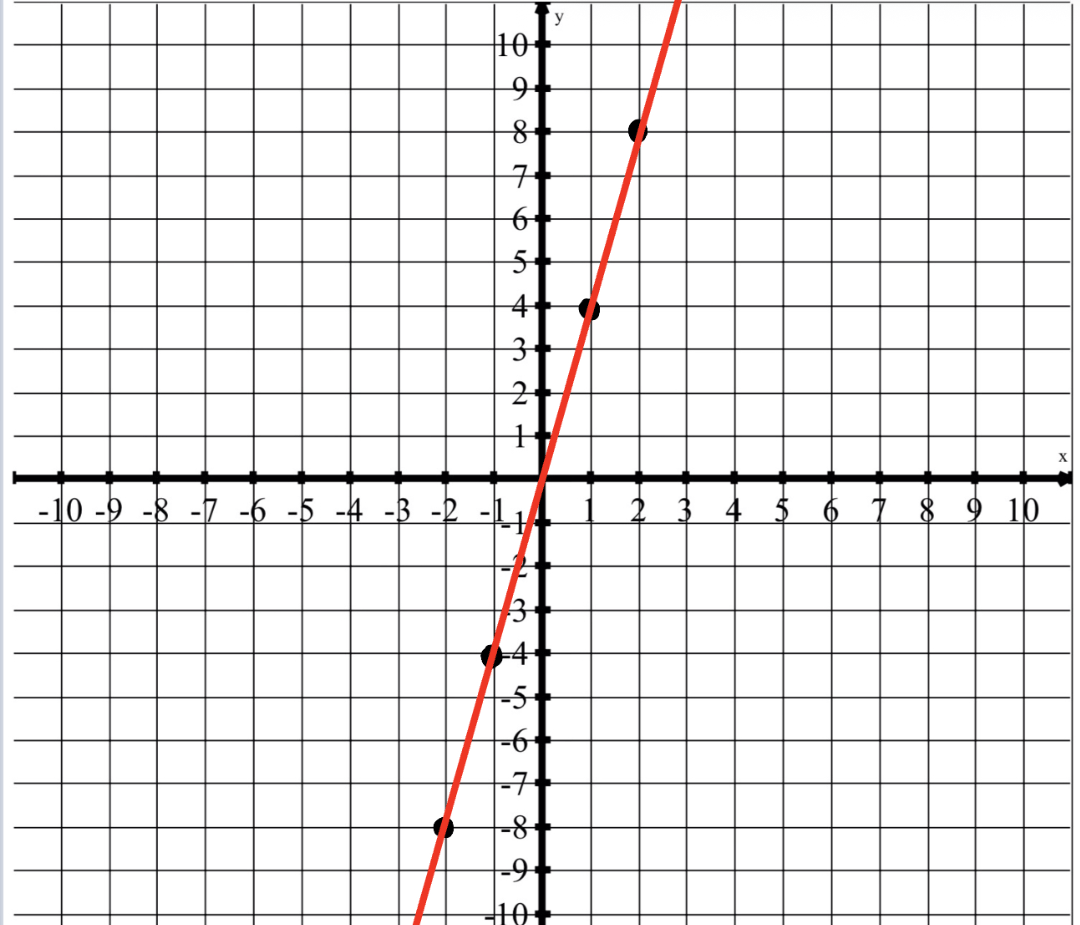
Write the equation in function form/slope-intercept form.
y = -18 - 2y + 5x
3y = 5x-18
(3y)/3=(5x)/3-18/3
y=5/3x-6
Find the x-intercept and y-intercept of -4x +12y=12. Write the x and y intercepts and write each as an ordered pair.
x = -3
(-3,0)
y= 1
(0,1)
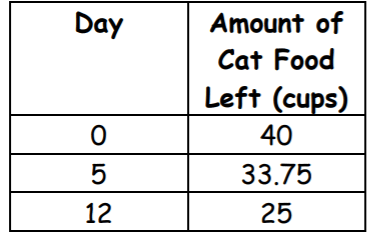
The graph is an example of a linear relationship. Identify and label the constant rate of change. Write the rate of change as an integer or decimal (a unit rate). SHOW YOUR WORK. Write the meaning of the rate of change in a sentence.
Bob works at Wegmans.
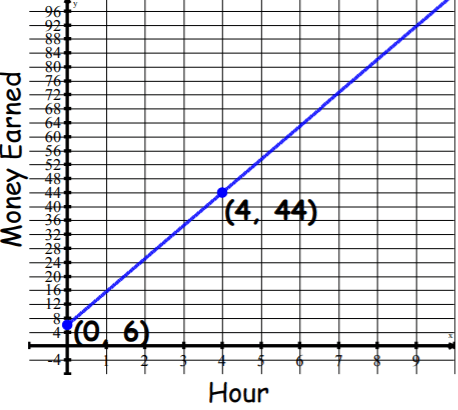
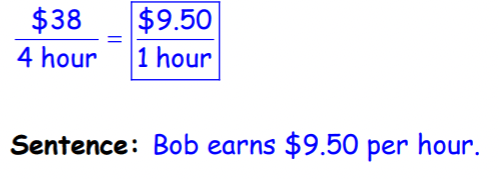
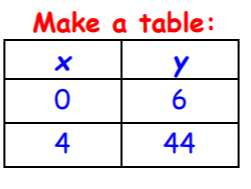
What is the slope of the line:
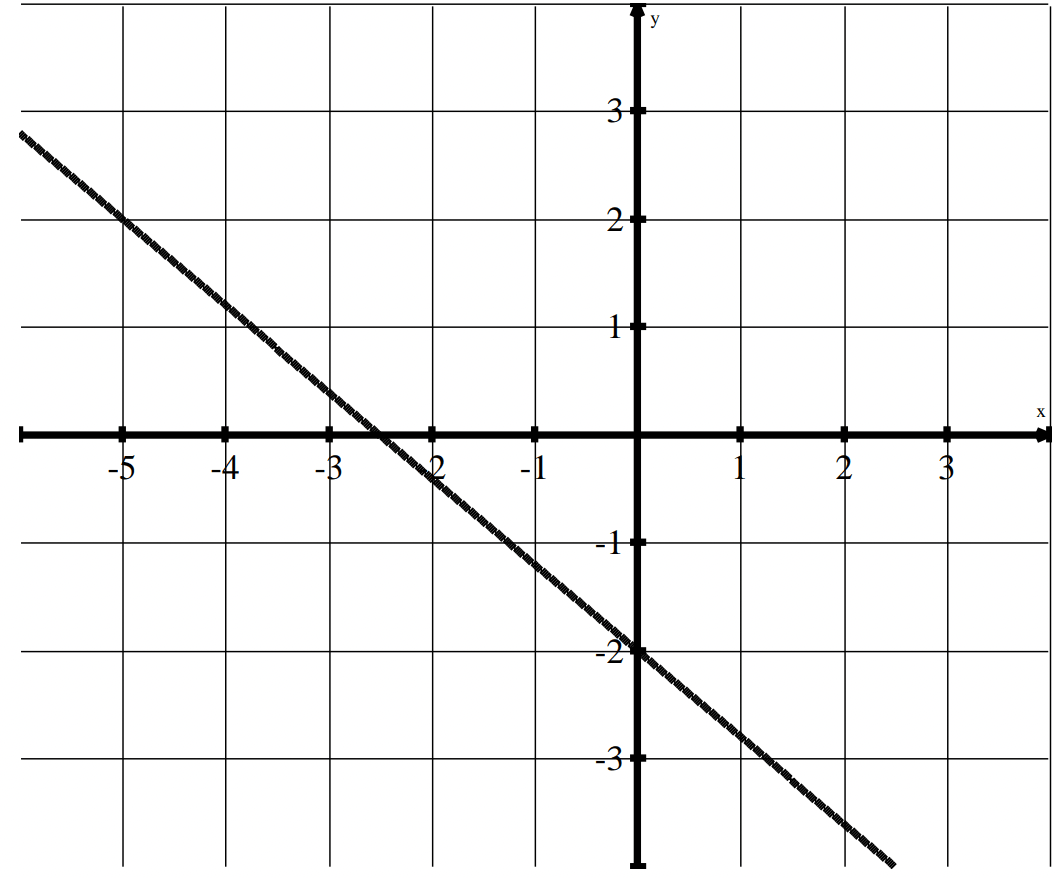
m=-4/5
What is the slope of the line:
-3x + y = 2
m=3
Write the equation in function form/slope-intercept form. Write all numbers as an integer, a reduced proper fraction, or a reduced improper fraction.
7x - 8y + 6 = 10 +2x
-8y+6=10+2x-7x
-8y=-5x+4
(-8y)/-8=(-5x)/-8+4/-8
y=5/8x-1/2
Find the intercepts of the equation. Write the x and y intercepts and write each as an ordered pair.
5y + 3x = 15
x = 5
(5,0)
y = 3
(0,3)
The graph is an example of a linear relationship. Identify and label the constant rate of change. Write the rate of change as an integer or decimal (a unit rate). SHOW YOUR WORK. Write the meaning of the rate of change in a sentence.
Bob bought a 40-cup bag of cat food. Each day, Bob feeds his cat the same amount of food.
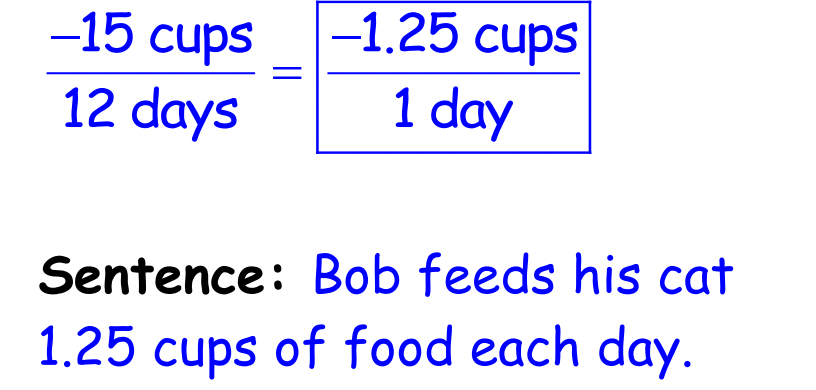
What is the slope of the line:
m=0
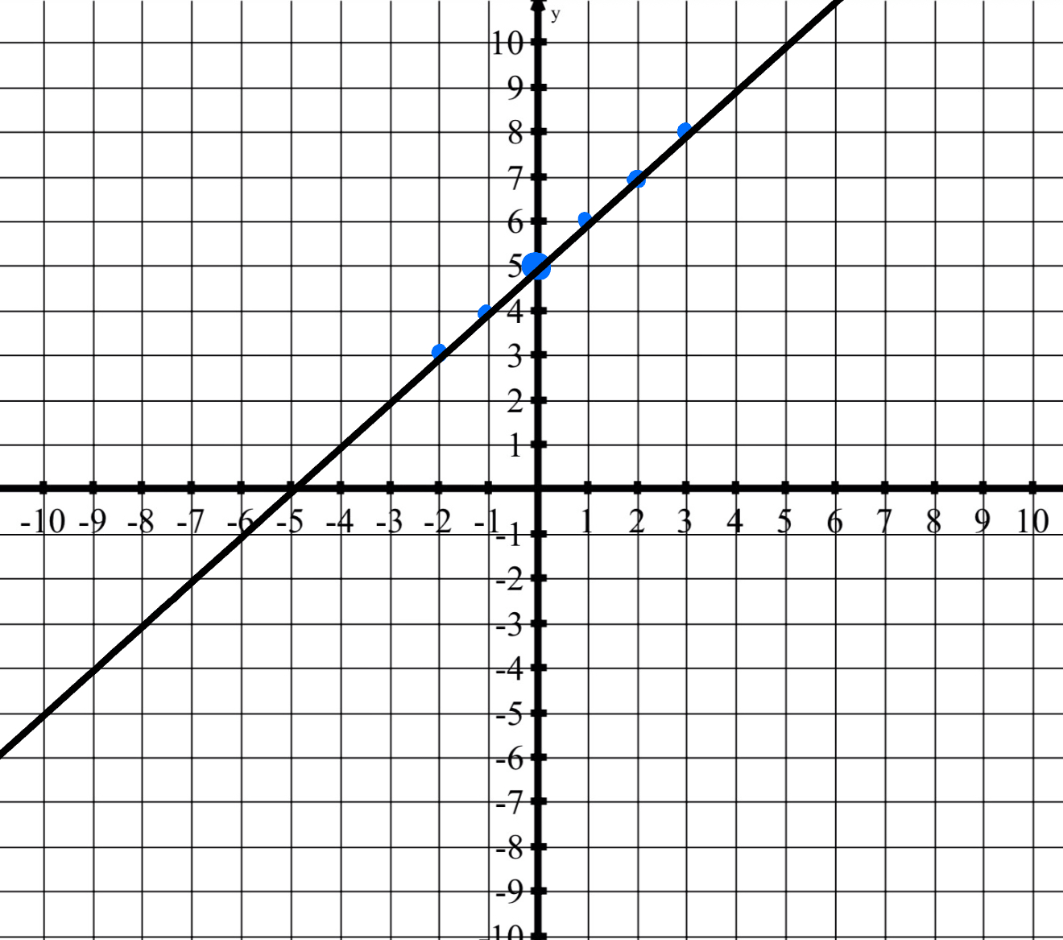
Identify the slope and y-intercept of of the line with the given equation. Use the slope and y-intercept to graph the equation.
y=x + 5
y-intercpet: y=5 (0,5)
slope: m=1
Write the equation in function form/slope-intercept form. Write all numbers as an integer, a reduced proper fraction, or a reduced improper fraction.
8y +8x -4 - 7y = 2(3x + 1 -2y)-4y
y+8x-4=6x+2-4y-4y
y=-2x+6-8y
9y=-2x+6
(9y)/9=-2/9x+6/9
y=-2/9x+2/3
Find the intercepts of the equation. Write the x and y intercepts and write each as an ordered pair.
7x - 9y = 63
x = 9
(9,0)
y = -7
(0,-7)
Determine whether the table represents a linear or nonlinear function. SHOW YOUR WORK. Provide an explanation.
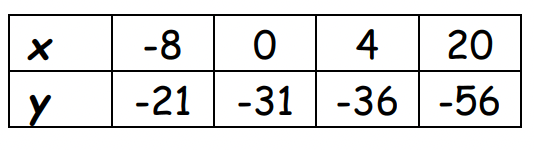
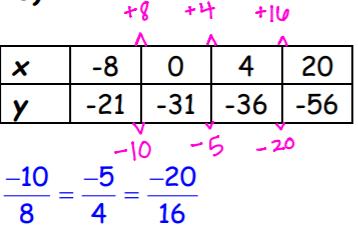
The table represents a linear function. The rate of change is constant.
Which line is the steepest? Which line is the most gradual? Be ready to explain yourself!
a. y=2x-1
b. y=1/2x+9
c. y=10x-5
d. y=1/10x+8
c. Steepest: y=10x-5
The biggest slope is 10 .
d. Most gradual: y=1/10x+8
The smallest slope is 1/10 .
Identify the slope and y-intercept of of the line with the given equation. Use the slope and y-intercept to graph the equation.
y=2-3/4x
y-intercept: y=2 (0,2)
slope: m=-3/4