Constant of Proportionality from Tables
Constant of Proportionality from Graphs
Constant of Proportionality from Words
Constant of Proportionality and Equations
Ratio Tables
100
Drew paints portraits. Find the constant of proportionality if it is a proportional relationship
Time (in hours) = x Number of portraits = y
1 5
2 10
3 15
4 20
5 portraits per hour
100
Find the constant of proportionality with correct units
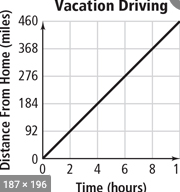
k =46 miles per hour
100
Morgan bought 24 batteries packed in 6 equal packs. What is the unit rate per pack
4 batteries per pack
100
What is k mean in y=kx?
constant of proportionality
100
A car is traveling at 55 miles per hour. How far does the car travel in 3 hours?
165 miles
200
The table shows the amount earned by Harry for selling ice cream. Find k.
Cups Sold = x 3 5 7 9
Earnings ($) = y 12 20 28 36
CoP = 4
200
Find the constant of proportionality with correct units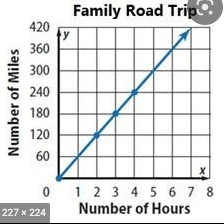
60 miles per hour
200
To make juice, Michael combines 4 liters of water and 12 scoops of juice mix. What is the CoP (scoops per liter)?
3 scoops per liter
200
Find the constant of proportionality:
C = 2/3 m
k = 2/3
200
A trail mix has a ratio of 2 M&Ms for every 3 almonds. Write three equivalent ratios for M&Ms to almonds.
Answers vary.
4:6
8:12
20:30
300
Fred wrote notes during an exam. Find the CoP (with correct units) if it is a proportional relationship.
Notes (pages) 8 9 10 11
Time (in hours) 18 19 20 21
It is not proportional, there is no CoP.
300
Find the constant of proportionality with correct units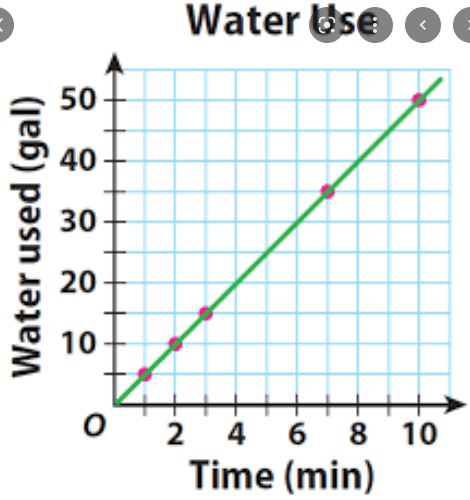
5 gallons per min
300
There are 100 centimeters in 1 meter. Use x to represent centimeters and y to represent meters and write two equations to represent the proportional relationship.
x = 100y
y = 0.01 x or y = 1/100 x
300
In a laboratory, scientists performed chemical reactions. The amount of product formed by a reaction can be determined by P = 0.5r, where P is the product and r is the amount of reactants used. Write an equation for r.
r = 2P
300
There are 35 calories in one serving of blueberries. How many calories are in 7 servings?
245 calories
400
A ferry transports bikes to an island. Write k (which is the CoP).
Number of bikes (x) 10 12 14
Number of trips (y) 5 6 7
k = 0.5
400
Find k with proper units.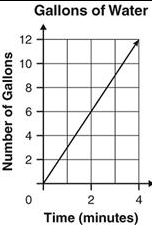
k = 3 gallons per minute
400
Write an equation that represents the following. Use "x" to represent feet, and "y" to represent inches.
There are 12 inches in 1 foot.
y = 12x
400
Daisy made bread. The equation b = 4f shows the number of breads (b) baked based on the amount of flour (f) used. Write an equation solving for flour. f = ?
f = 1/4b or f = 0.25b
400
16 servings of strawberries is 720 calories. How many servings is 112.5 calories?
Hint: start with the CoP
2.5 servings
500
Alice bought comics. Finish the ratio table and the k (CoP with correct units) if the table shows a proportional relationship.
Number of comics 2 4 ?
Price (dollars) 5 ? 15
6, 10 and k = 2.5 dollars per comic
500
DAILY DOUBLE
What is K with proper units?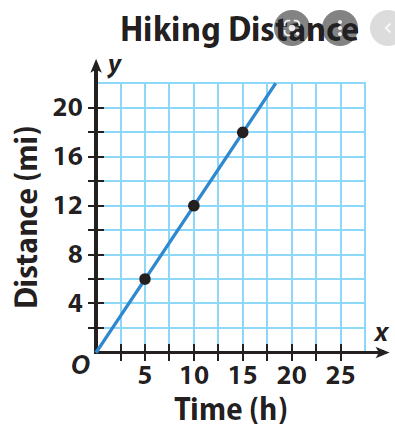
DAILY DOUBLE
k = 1.2 miles per hour
500
Julie brought 5 pounds of cans to a recycling place and was paid $2. Find the constant of proportionality (cost per pound)
$0.40/pound
500
Write an equation that represents the following scenario. Use "d" to represent distance, and "t" to represent time.
Mitchell rides his bike at a speed of 3.5 miles per hour.
d = 3.5t
500
See Mrs. Kohagen's slideshow for this ratio table question.
N/A