Inductive Reasoning
Conditional Statements
Deductive Reasoning
Properties
Algebra in Geometry
100
Look for a pattern. What are the next two terms in the sequence?
55, 44, 33, 22, ...
11, 0
100
p -> q
Conditional Statement
100
If the hypothesis of a true conditional is true, then the conclusion is true.
Law of Detachment
100
a = a
Reflexive Property of Equality.
100
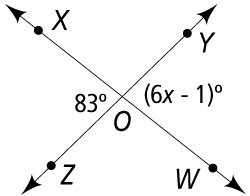
Solve for X.
x = 9
200
A conclusion you reach using inductive reasoning.
Conjecture
200
q -> p
Converse
200
Allows you to state a conclusion from two true conditional statements when the conclusion of one statement is the hypothesis of the other statement.
Law of Syllogism
200
If ∠A ≅ ∠B, then ∠B ≅ ∠A.
Symmetric Property of Congruence.
200
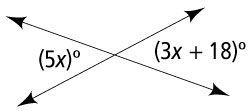
Solve for x.
x = 14.
300
An example that shows that a conjecture is incorrect.
Counterexample
300
~p -> ~ q
Inverse
300
The process of reasoning logically from given facts to reach a conclusion.
Deductive Reasoning
300
If a = b and b = c, then a = c.
Transitive Property of Equality.
300
Two angles that add to 90 degrees
Complementary Angles
400
Equivalent Truth Values
Conditional and Contrapositive AND
Converse and Inverse
400
~q -> ~p
Contrapositive
400
What can you conclude from the given information? If Karl runs 1 mi, then he runs 1760 yd. If Karl runs 1760 yd, then he runs 5280 ft.
If Karl runs 1 mi, then he runs 5280 ft.
400
Used to justify equal numbers.
Properties of equality.
400
Two angles that sum to 180 degrees.
Supplementary Angles
500
Three components of a good definition.
Clearly understood terms, Precise, Reversible
500
A single true statement that combines a true conditional and its true converse. Uses the phrase, “if and only if.”
Biconditional
500
What can you conclude from the given true statement? If you want to buy the school lunch today, then you will need $2.50. You brought $2.50 to school today.
No Conclusion.
500
Used to justify congruent geometric figures.
Properties of Congruence.
500
Pairs of opposite angles made by two intersecting lines.
Vertical Angles