State which of the pictures are similar to the picture shown. If the image is similar, state whether the image was reduced or enlarged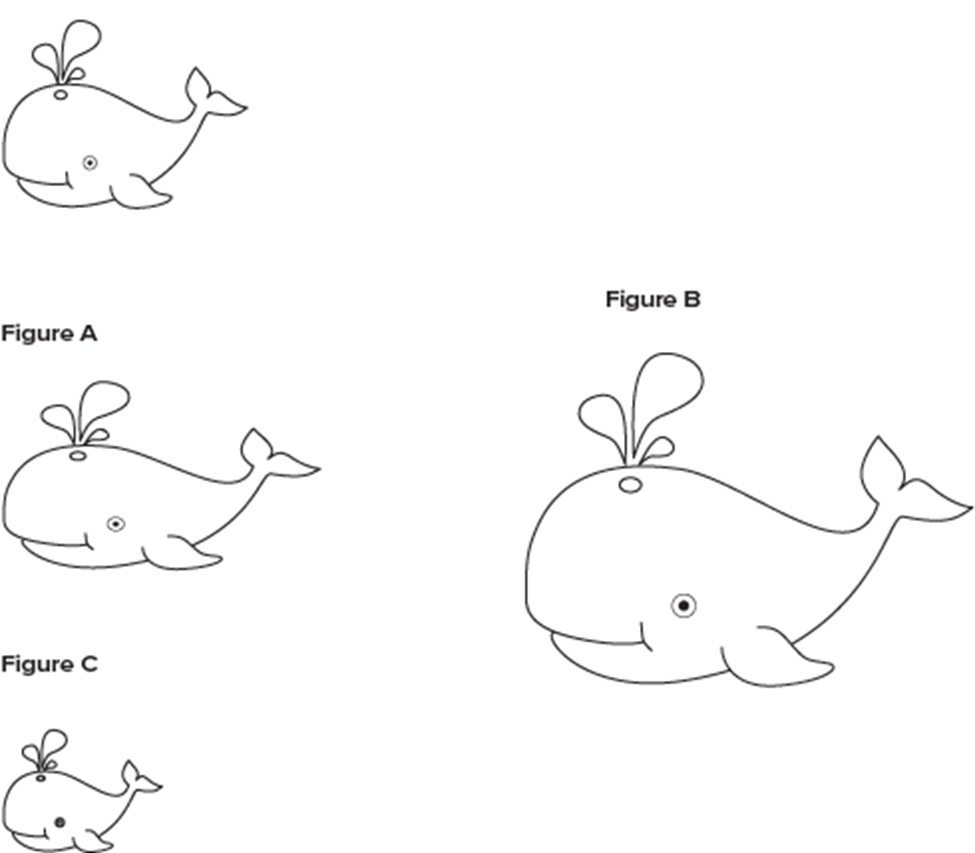
Figure A Figure B and Figure C are similar.
Figure C is a reduction and Figure A & B are enlargements
Describe the three possible rigid motion transformations that can be used to move a figure on the coordinate plane. Explain in your own words the meaning of dilation.
Reflection, Rotation, Translation
Dilation to create a similar figure that is either smaller, larger, or the same size as the original figure.
Rectangle QRST has the following coordinates Q(-3,7), R(-3,11), S(4,11) and T (4,7)
Dilate the rectangle by a scale factor of 3 with a center of dilation at (0,0). List the new coordinates
Q' (-9,21) R' (-9,33), S' (12, 33), and T' (12,21).
Consider square ABCD. Side AB is 5 cm, side BC is 5 cm, side CD is 5 cm, and side DA is 5 cm. You dilate the square using a scale factor of 1. Is the resulting image congruent, similar, or both?
True
1. A figure dilated using a scale factor >1 is a ______________.
2. A figure dilated using a scale factor <1 is a ______________.
3. A figure dilated using scale factor of 1 is both ________________ and _______________.
1. enlargement
2. reduction.
3. congruent and similar.
Describe the sequence of transformations that are needed to map ABC onto A'B'C'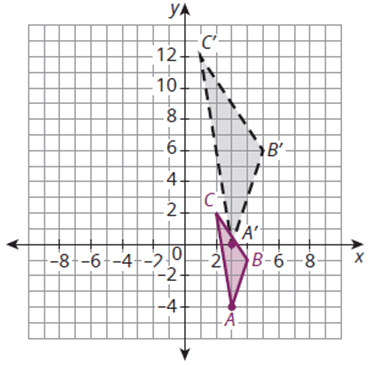
Translate vertically 4 units, dilate using a scale factor of 2 and point A as the center of dilation.
Trapezoid FGHI has the coordinate F (4,4), G (4,8), H (12, 8), and I (12,4). Dilate the trapezoid using a scale factor of 1/4 with a center of dilation at the origin. What are the coordinates of trapezoid F'G'H'I'?
F' (1,1) G' (1,2), H' (3,2), and I' (3,1).
<F corresponds to <N
<R corresponds to <O
<Y corresponds to <W
Similar figures are always are congruent figures.
False, if the sizes are different, the figures cannot be congruent
Scale factor = 4.5
Describe a sequence of transformations that exhibits the similarity between the pair of figures shown.
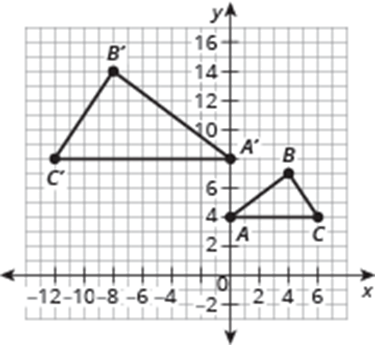
Triangle ABC reflects across the y-axis, then dilates by a scale factor of 2 with the origin as the center of dilation.
Explain the difference between dilating a figure using the origin and dilating a figure using a center of dilation not at the origin.
When we dilate a figure using the origin as our cod, we can multiple the vertices by the scale factor.
When the cod is not (0,0), first we must subtract the cod from our original x,y, then we must multiple the scale factor, and then we must add the cod to the coordinates to find the coordinates of our dilated figure.
Suppose that triangle FAR is similar to triangle SUN
- Identify the corresponding angles and state the relationship between the angles (similar, congruent, or both?)
<F is congruent and similar to <S
<A is congruent and similar to <U
<R is congruent and similar to <N
To find the scale factor, you divide the old figures dimensions by the new figures dimensions.
False, the basic formula to identify the scale factor is the new dimensions divided by the old dimensions
Describe the dilation needed to map the pre-image onto the image. Pre-image: Triangle ABC, Image: A'B'C', center of dilation, A. Scale factor: ?
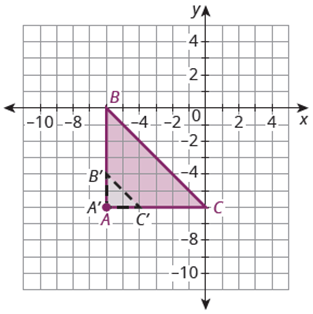
(2 divided by 6)
Side A'B' is 2 units
Side AB is 6 units
Pre-image: ABC
Image: A'B'C'
Describe the rigid motion transformation and dilation needed to map the pre-image onto the image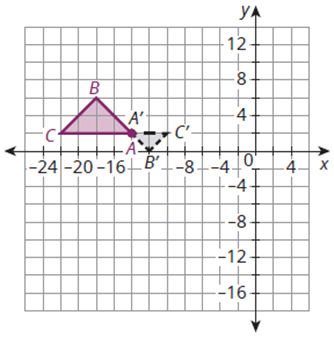
Rotate 180 degrees about A. Dilate the triangle using A as the center of dilation and a scale factor of 1/2.
Triangle ABC has vertices with coordinates A(2,5) B (4,2) and C (2,2). Dilate ABC on the coordinate plane using point C as the center of dilation and a scale factor of 3 to form triangle A'B'C'. List the new coordinates and state whether the dilation is an enlargement or a reduction.
Enlargement
New coordinates, A' (2,11) B' (8,2), and C' (2,2)
Suppose that triangle FAR is similar to triangle SUN. Identify the corresponding sides of the triangles and state the relationship between the lengths of the corresponding sides.
Side FA/SU is congruent to AR/UN is congruent to FR/SN
The angles of dilated figures are congruent to the original figure.
True
Triangle ABC is dilated using a scale factor of 5. Write the coordinates of the vertices after a dilation with a scale factor of 5, centered at the origin.
The original coordinates are A (-1,0) B (-1,1) C (0,2)
A'(-5,0)
B'(-5,5)
C'(0,10)
Consider Rectangles ABCD and EFGH. Describe a sequence of transformations that maps ABCD onto EFGH. You will need to perform a rigid motion transformation and then dilate the figure for the shapes to map onto each other. No points will map onto each other before the transformation. 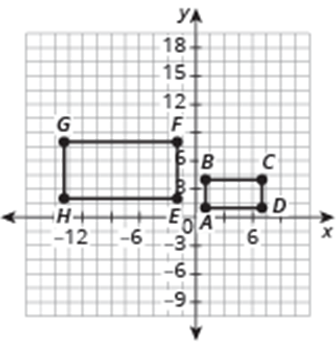
Reflect ABCD across the y-axis, then dilate the rectangle by a scale factor of 2. COD was (0,0).
Triangle ABC has vertices with coordinates A(3,1) B (4,8), and C (11,6).
Dilate ABC on the coordinate plane using point M (0,2) as the center of dilation and a scale factor of 1/2 for form A'B'C'. List your coordinates and plot the triangles on a graph. *USE Graph Paper*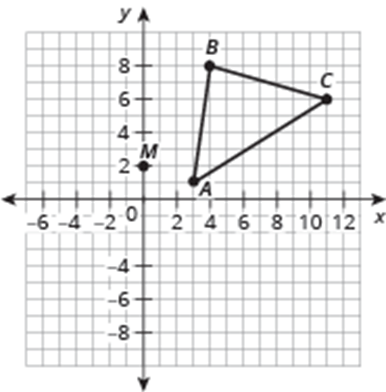
A' (1.5,1.5)
B' (2,5)
C' (5.5, 4)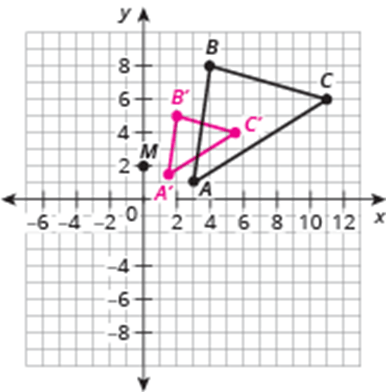
Figure WXYZ was dilated using a scale factor of 1/2 to create figure W'X'Y'Z'. Figure W'X'Y'Z' was dilated using a scale factor of 2 to create figure W"X"Y"Z". Is figure W"X"Y"Z" congruent and similar to figure WXYZ?
Yes, the figures WXYZ and W"X"YZ" are congruent and similar.
A rigid transformation always results in congruent figures.
True! Remember rigid motion transformations preserve the figure's size and shape. (Reflection, rotation, and translation.