Random
Am I a function?
What's my function?
Evaluate Function finding f(x)
Graph What?
100
Determine if the given relationship is a function. Explain your answer.
This is a function because a function means that every input has exactly one output.
100
In a function, how many outputs can one input have?
Each input has one and only one output.
100
Evaluate y = 2x +1 when x = -3
y = -5
100
Evaluate f(x) = -4x + 5, when f(10)
f(10) = -35
100
Based on the graph of function, evaluate for f(2)?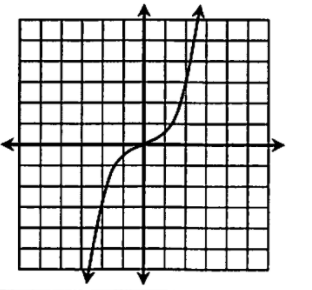
y = 3
200
Determine if the given relationship is a function. Explain your answer.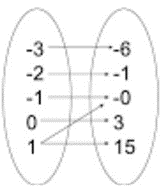
This is not a function because the input 1 has two outputs.
200
Yes
200
Evaluate f(x)= 2x + 1 when f(-5)
-9
200
Evaluate f(x) = 3x - 2, when f(5)
f(5) = 13
200
Based on the graph of function, evaluate for f(-5)
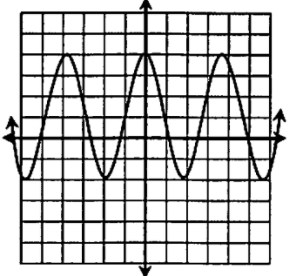
y = 0
300
Determine if the given relationship is a function. Explain your answer.
This is a function because the graph passes the vertical line test.
300
Is this a function and why?
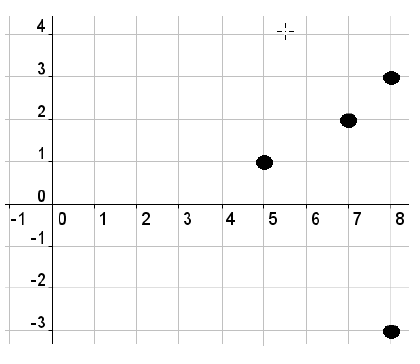
No because x=8 has two outputs (3 and -3)
300
Evaluate f(x) = 6 - x when f(-7)
f(-7) = 13
300
Evaluate f(x) = 2x - 6, when f(-10)
f(-10) = -26
300
Based on the graph of the function, evaluate forf(4)
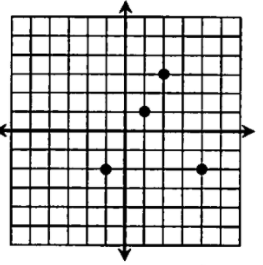
y = -2
400
Determine if the given relationship is a function. Explain your answer.
(-2, 1)
(-2, 3)
(0, -3)
(1, 4)
(3, 1)
This is not a function because the input -2 has two outputs.
400
Does the following table represent a function?
x y
1 2
2 5
6 2
2 9
5 1
No, because the input (x) of 2 has two different outputs (y)
400
Evaluate f(x)= 4x - 1 when f(x)= -17
x = -4
400
Evaluate g(x) = x2 + 5, when g(2)
g(2) = 9
400
Based on the function, evaluate for f (-3)? Also find the domain and range for both
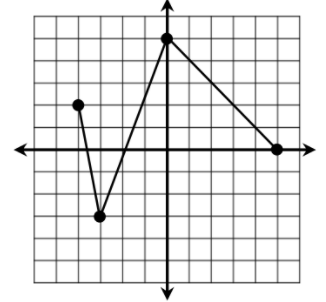
y = -3
500
The Flu is spreading through Columbia. The function below determines how many people have swine where t = time in days and S = the number of people in thousands. S(t) = 9t - 4. Find S(4).
S(4) = 32
500
No, vertical lines are not functions.
500
f(x) = -x + 8; evaluate f(x)=2
x = 6
500
Evaluate g(x) = x2 - 10, when g(-5)
g(-5) = 15
500
Based on the function, evaluate for f(2). Challenge find the Domain
f(2)=0
infinity