Ice Cream & Party Hats
Tin Cans & Telephone Poles
Funciones 1
Funciones 2
Funciones 3
100
The volume of a cone that has a radius of 5 inches and a height of 12 inches. V= 1/3πr^2h
314 inches cubed
100
The volume of a cylinder whose radius is 4 feet and whose height is 3 feet. V= πr^2h
150.72 ft cubed
100
D y E
100
El teléfono inteligente de Lin estaba completamente cargado cuando ella comenzó la escuela a las 8:00 a.m. A las 9:20 a.m., estaba cargado en un 90%, y al mediodía estaba cargado en un 72%.
¿Cuándo crees que su batería se agotará?
¿Es la vida de la batería una función del tiempo? Si así es, ¿es esta una función lineal? Explica tu razonamiento.
- Ejemplo aproximadamente a las 9:20 p.m. (como el 10 por ciento de la batería se perdió en 80 minutos, tomaría 800 minutos perder toda la batería.
- La batería que queda es una función del tiempo pero no una función lineal.
100
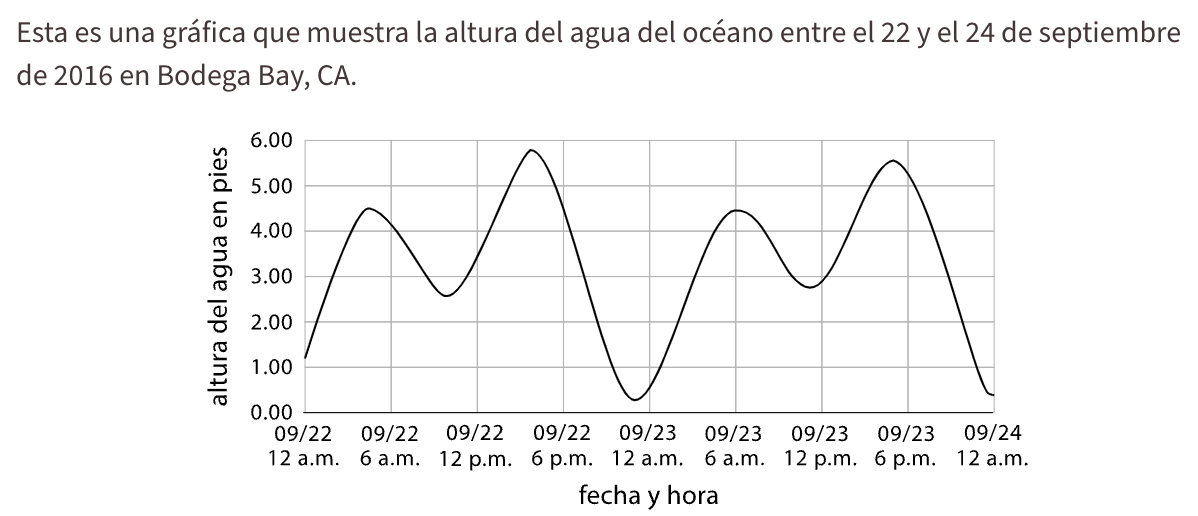
1. Estima la altura del agua a las 12 p.m., el 22 de septiembre
2. ¿Cuántas veces el agua alcanzó una altura de 5 pies?
3.5 pies aproximadamente
4 veces.
200
You get a snow cone at the fair. The paper cone you get has an opening of 2 inches in diameter and is 5 inches tall. It is really hot outside and your snow cone melts! What is the approximate volume of the melted sugar water in your paper cone?
5.2 inches cubed
200
El volumen de un cilindro es 1063.48 pulgadas3, y su altura es de 14.7 pulgadas. Encuentra su diámetro
Aproximadamente 9.6 pulgadas
200
Dada la ecuación
y=-4x+3.5
- Cuando x es 1, ¿qué valor de y hace verdadera la ecuación?
- Cuando x es -1.5, ¿qué valor de y hace verdadera la ecuación?
- Cuando y es 7.5, ¿qué valor de x hace verdadera la ecuación?
-0.5
9.5
-1
200
La suma del área de los rectángulos es 30 centímetros cuadrados.
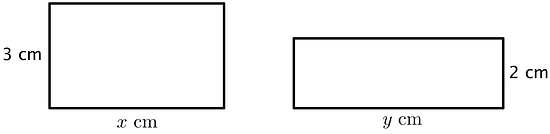
- Escribe una ecuación que muestre la relación entre x e y.
3x + 2y = 30
200
La gráfica representa el volumen de un cilindro que tiene una altura igual a su radio.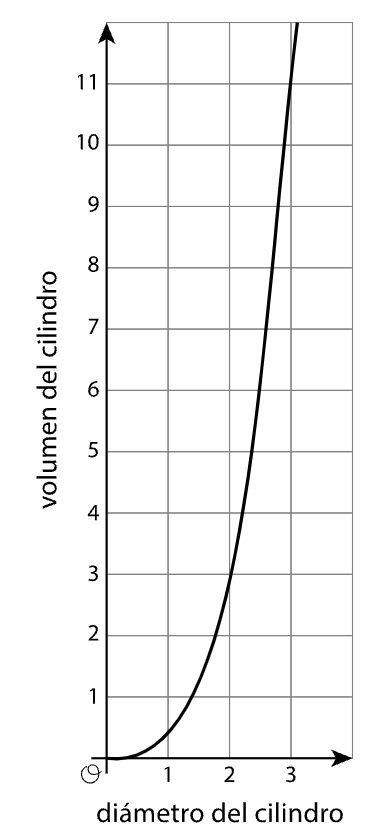
1. ¿Es el volumen del cilindro función del diámetro? ¿Por qué?
Si, para cada diámetro hay un único volumen
300
El volumen de un cono 83.60 mm3 y su radio es 2 mm. Calcula la altura
aproximadamente 6.66 mm
300
Emma Stone decides to start saving water by collecting rain in a barrel. Emma Stone buys a barrel 2 feet across and 3.5 feet tall. What is the total volume of rain that Emma Stone can collect?
Aproximately 10.99 cubic feet
300
La gráfica representa el precio promedio de la gasolina corriente en los Estados Unidos (en dólares) como una función del número de meses después de enero de 2014.
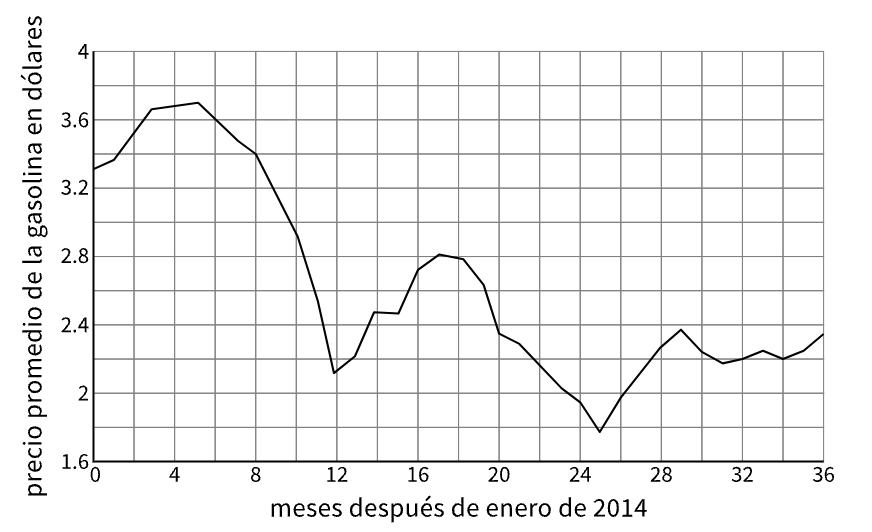
- ¿Cuántos meses después de enero de 2014 se presentó el precio más alto de la gasolina?
- ¿En algún momento el precio promedio de la gasolina estuvo por debajo de $2?
1. A los 5 meses
2. Si, durante los meses 24, 25 y 26
300
Para la función que representa la siguiente ecuación 3x + 2y = 30. Rellena los valores que faltan en la tabla
300
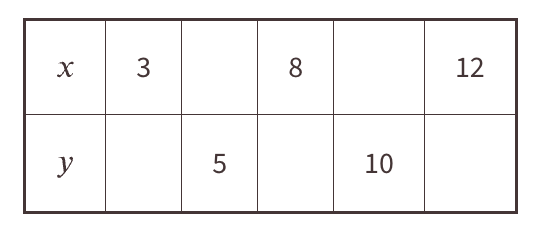
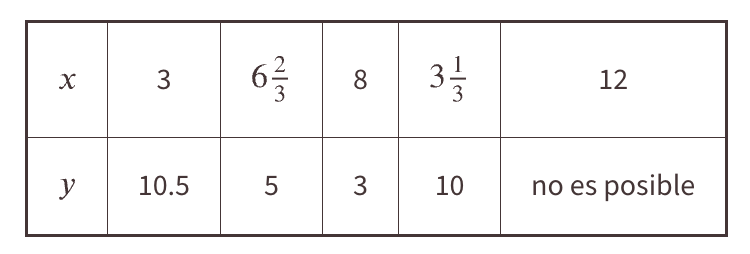
La tabla y la gráfica representan dos funciones. Usa la tabla y la gráfica para responder las preguntas.
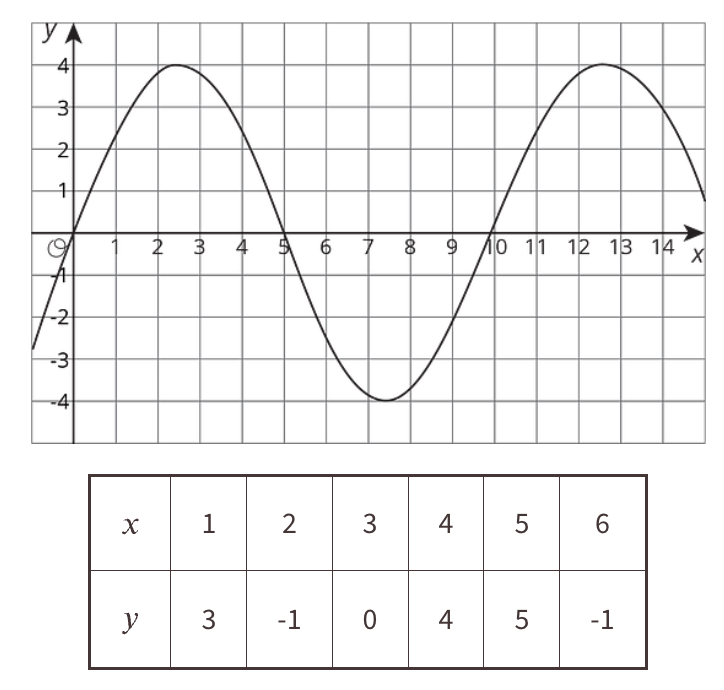
- ¿Para cuáles valores de x la salida de la tabla es menor que la salida de la gráfica?
- En la función representada en la gráfica, ¿cuáles valores de x dan una salida de 0?
2 y 3
0, 5 y 10
400
You visit two ice cream shops, and both have delicious waffle cones. They both charge the same amount for the cones, but they are different sizes. Shop A's cones are 3 inches in diameter and 8 inches tall. Shop B's cones are 2.5 inches in diameter and 9 inches tall. Which shop gives you more ice cream?
What is shop A?
400
Un cilindro tiene volumen de
45pi unidades cúbicas
y radio 3 unidades. ¿Cuál es su altura?
5 unidades
400
Tim revisa con un par de amigos que tienen el mismo tipo de teléfono para ver cuántas imágenes tienen en sus teléfonos y cuánta memoria ocupan. Los resultados se muestran en la tabla.
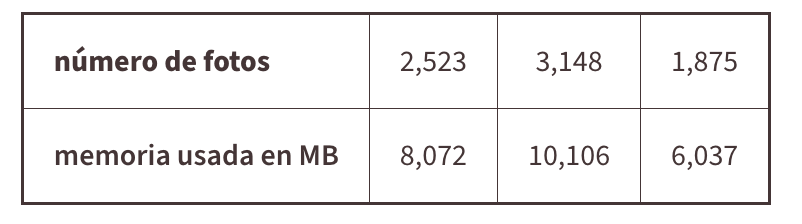
- ¿Se podría modelar esta información razonablemente con una función lineal? Redondea la pendiente a la décima
- Elena necesita borrar fotos para crear 1,200 MB de espacio. Estima el número de fotos que debe borrar.
1. Si, todos los puntos están cerca de y=3.2x, donde x es el número de fotos e y la cantidad de memoria usada
2. Aproximadamente 375 fotos
400
Selecciona todos los puntos que están sobre una recta que tiene pendiente 2 y que también contiene al punto (2,-1)
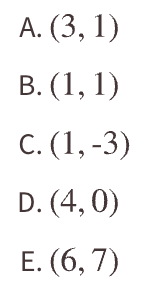
A, C y E
400
Dos estudiantes entran a un club de resolución de rompecabezas y se vuelven más rápidos para terminar los rompecabezas a medida que practican más. El estudiante A mejora sus tiempos más rápido que el estudiante B.
- Empareja los estudiantes con las rectas l y m .
- ¿Cuál estudiante ERA más rápido en la resolución de rompecabezas antes de la práctica?
1. Estudiante A = recta l
Estudiante B = recta m
2. Estudiante B