Solve for u.
8u+14=5u+6u-10
u=8
Explain how to graph
y=-2/5x+5
Find the average rate of change for the number of bacteria from 3.4 hours to 8.5 hours.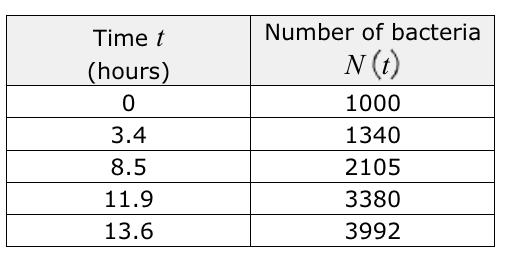
150 bacteria per hour
Explain how to graph
y> -1/2x-3
Start at -3. Go down 1 & right 2 (or up 1 & left 2).
DASHED line. Shade ABOVE.
Solve for x.
6x+2(x-2)=-36
x=-4
#1) At what height is the temperature 0oC?
#2) At what rate is the temperature increasing/decreasing?
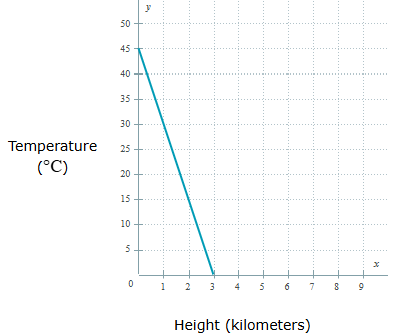
#1) 3 km
#2) DECREASING at a rate of 15oC per km (not -15oC)
Explain how to graph
x-y=-4
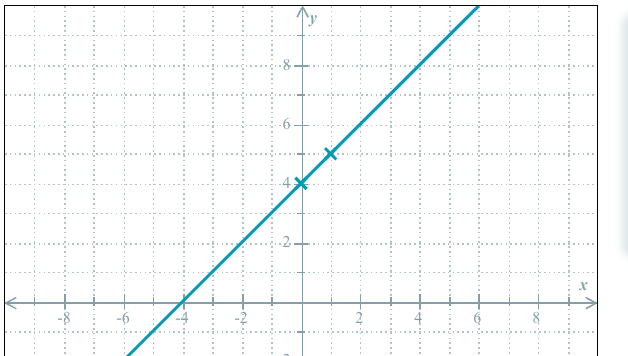
Describe how these graphs would be DIFFERENT:
Line 1: y>2/3x-1
Line 2: y=2/3x-1
Line 1 is DASHED & Line 2 is SOLID.
Line 1 has SHADING & Line 2 has NO SHADING.
Solve for a.
(3x+20)/4=2
x=-4
Alan has 11 new magazines to read.
Let M be the number of magazines he would have left to read after reading R of them.
Write an equation relating M to R.
" y=11-1x "
M=11-R
For the 25 students surved:
#1) as the time spent texting increases, the time spent exercising tends to ___________
#2) there is a ___________ correlation between time spent texting and exercising
#3) Using the line of best fit, we would predict that a student texting for 6 hours would exercise for approximately: _____
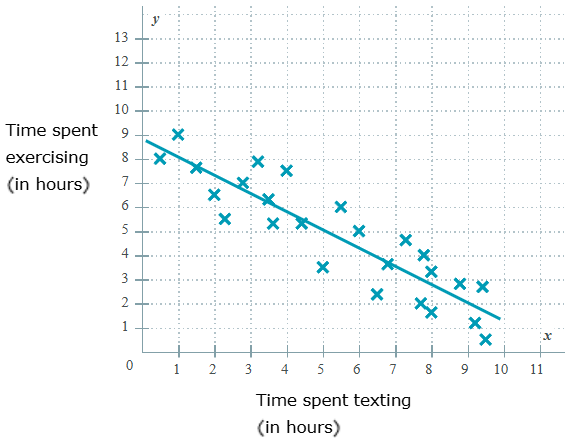
#1) DECREASE
#2) NEGATIVE
#3) ~4 hours exercising
Solve for x.
-7(x+2)+9>=3(9-y)
x<=-8
Solve for v.
-1=8+v/3
v=-27
Find the 60th term of the following arithmetic sequence.
17,23,29,35,...
a_n=17+6(n-1)
a_n=11+6n
a_60=371
Use the equation of the line of best fit, y=-0.76x+26.04, to give EXACT answers.
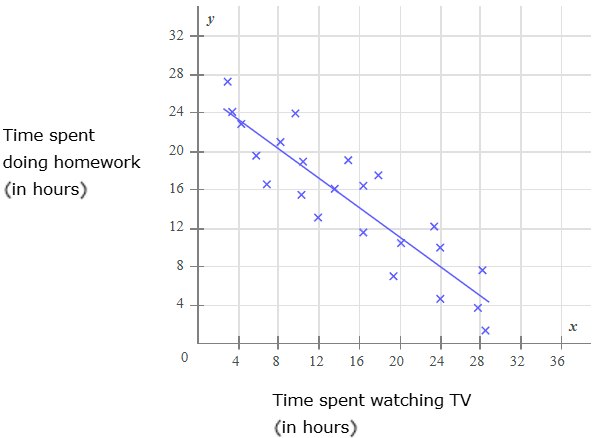
#1) What is the predicted time spent doing homework for a student who spends 12 hours watching TV?
#2) What is the predicted time spent doing homework for a student who doesn't spend any time watching TV?
#3) For an increase of one hour in the time spent watching TV, what is the predicted decrease in the time spent doing homework?
#1) 16.92
#2) 15.72
#3) 0.76 (always positive)
Lucy's fish tank has 14 liters of water in it. She plans to add 6 liters per minute until the tank has less than 56 liters. What are the possible numbers of minutes Lucy could add water?
Use t for the number of minutes. Write your answer as an inequality solved for t.
14+6t<56
t<7
Deshaun will rent a car for the weekend. He can choose one of two plans. The first plan has an initial fee of $70 and costs an additional 60 cents per mile driven. The second plan has no initial fee but costs 70 cents per mile driven. How many miles would Deshaun need to drive for the two plans to cost the same?
700 miles
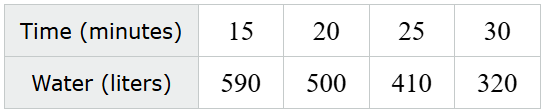
#1) The rate of the water is: ____________ by ____
#2) How much water was in the vat when the workers started draining it?
#1) DECREASING by 18 liters per minute (-90/5=-18)
#2) 860 liters
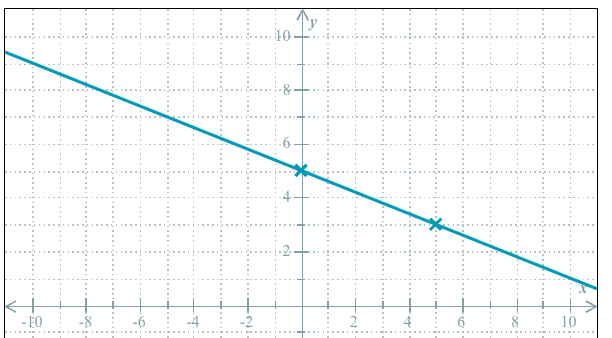
Write the equation of the line that goes through the two points (4, -3) and (-2, -1).
y=-1/3x-5/3
y+1=-1/3(x+2)
y+3=-1/3(x-4)
Alan wants to earn at least $66 trimming trees. He charges $7 per hour and pays $4 in equipment fees. What are the possible numbers of hours Alan could trim trees?
Use t for the number of hours. Write your answer as an inequality solved for t.
7t-4>=66
t>=10