Compound Events
Two Way Tables
Venn Diagrams
Determining Independence
100
You flip a coin and spin a spinner that is split into 4 equal sections (labeled 1, 2, 3 and 4). How many possible outcomes are there in this experiment?
8
100
What is the probability that a randomly selected person likes football?
42/72 = 0.58333
100
How many people were surveyed?
348
100
How do we determine if two events are independent?
P(A)=P(A|B)
or
P(B)=P(B|A)
200
You flip a coin and spin a spinner that is split into 5 equal sections (labeled 1, 2, 3, 4 and 5). List all possible outcomes for this experiment.
H1. H2. H3. H4. H5
T1. T2. T3. T4. T5
200
What is the probability that a randomly selected student plays football?
33/100 = 0.33
200
Find P(G).
85/348 = 0.5316
200
Are the events "version 1" and "likely to buy" independent? Why or why not?
Not independent
P(A)= 99/180 = 0.55
P(A|B)= 25/65 =0.385
300
You flip a coin and spin a spinner that is split into 4 equal sections (labeled 1, 2, 3 and 4). What is the probability that the coin lands on heads and you spin a 3?
1/8
300
What is the probability that a randomly selected female plays basketball?
16/52
300
Find P(G and H)
22/348 = 0.0632
300
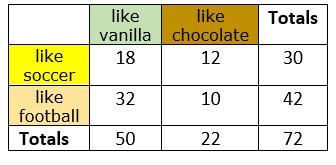
Are the events "likes football" and "likes chocolate" independent? Why or why not?
Not independent
P(A)= 42/72 =0.583333
P(A|B)=10/22 = 0.4545
400
You flip a coin and spin a spinner that is split into 5 equal sections (labeled 1, 2, 3, 4 and 5). What is the probability that the coin lands on tails and the spinner lands on a number greater than 2?
3/10
400
What is the probability that a randomly selected person who prefers vanilla also prefers soccer?
18/50
400
Find P(G|H)
22/170 = 0.1294
400
Are the events "H" and "G" independent?
Why or why not?
Not independent
P(H) = 170/348 = 0.4885
P(H|G) = 22/185 = 0.1189
500
You flip a coin and spin a spinner that is split into 5 equal sections (labeled 1, 2, 3, 4 and 5). What is the probability that the coin lands on heads or the spinner lands on an odd number?
8/10 or 4/5
500
What is the probability that someone who viewed the 2nd version is likely to buy?
20/30
500
Find P(H|G)
22/185 = 0.1189
500
Are the events "fresh" and "apples" independent? Why or why not?
Not independent
P(A)= 320/415 = 0.77
P(A|B)= 40/70 = 0.57