Factor
x^2-196
(x-14)(x+14)
Define domain.
The set of x values a function can take.
Calculate
log_3(9)+log_2(16)
6
Find
sin(270^o)
-1
Find the area of a triangle with side lengths 20 ft, 10 ft and included angle 30 degrees.
50 ft2
Factor
6x^2+11x-10
(3x-2)(2x+5)
Given the function below, state its domain and range.
f(x)=x^2-7
Domain is all real numbers, range is
{y|y>=-7}
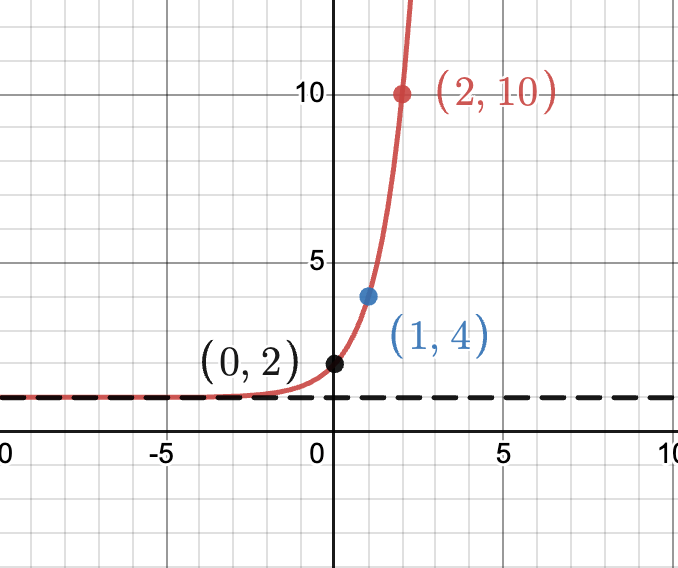
Sketch, clearly indicating the asymptote and 3 other points on the graph
y=3^x+1
Name an angle co-terminal to
45^o
45^0 + k360^0
Sketch for , indicating max, min, midline, and period
0<=x<=16pi
y=2sin(x/4)+5

Complete the square:
3x^2-4x+5
3(x-2/3)^2+11/3
Graph the function below, indicating all axes intercepts and asymptotes.
(x-4)/(x+2)
Vertical asymptote at x = -2, Horizontal asymptote at y = 1, x - intercept at (4, 0) and y - intercept at (0, -2)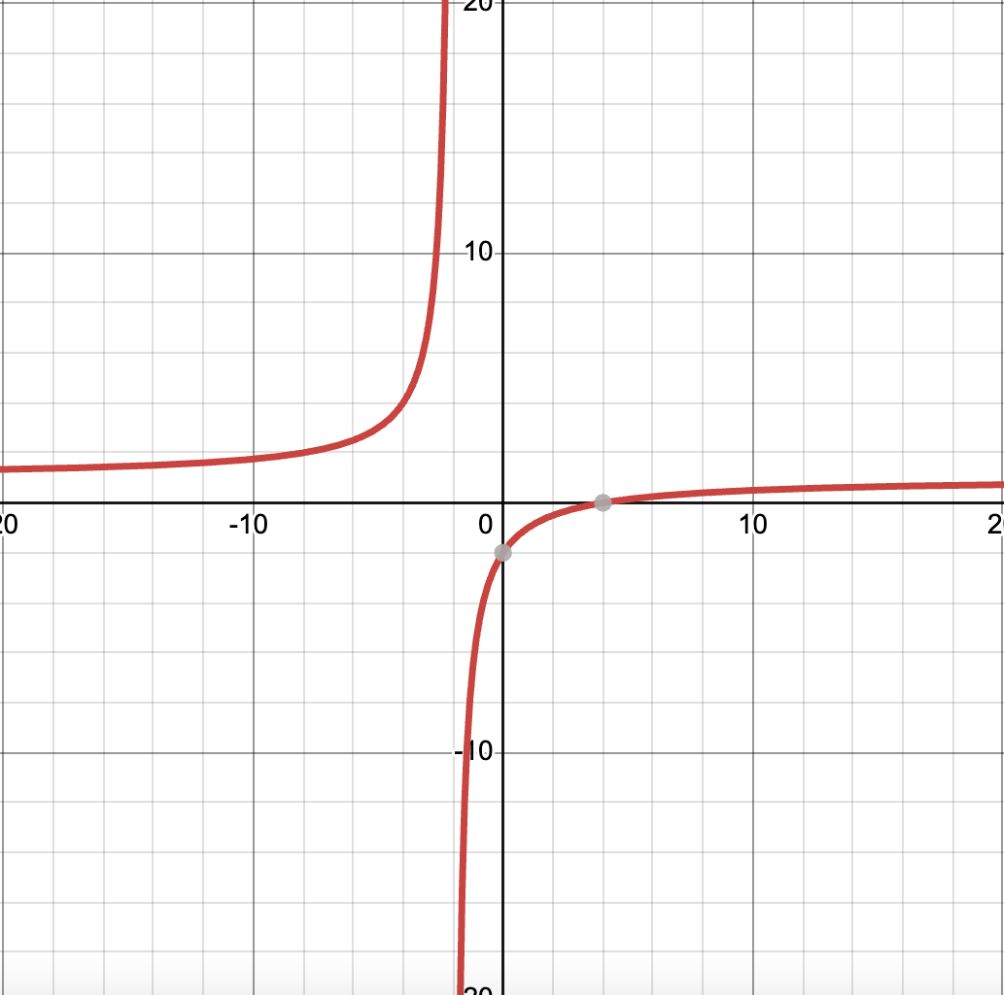
In 1985, there were 285 cellphone subscribers in a small town. The number of subscribers increased by 75% per year after 1985. How many cellphone subscribers were there in 1994?
43, 872 subscribers
Find the values of x in radians for
-pi/2<=x<=pi/2
tan^-1(1)=x
pi/4
Find the possible values of the included angle of a triangle with sides of length 8 and 5, and area 15cm2
sin-1(15/20) = 48.6 degrees or 131.4 degrees.
Find, in the form
y=ax^2+bx+c
, the equation of the quadratic whose graph touches the x-axis at 4 and passes through (2, 12)
y=3x^2-24x+48
What is the range of
4sin(x)-2
The range is
{y|-6<=y<=2
Write as a log base 3 and simplify.
log_9(t)
log_3(t)/log_3(9)
=
(log_3(t))/2
=
(1/2)log_3(t)
=
log_3(sqrtt)
Find two angles (in RADIANS) on the unit circle, for
0<=x<=2pi
, such that
cos(x)=-2/3
(CALCULATOR ON)
x = 2.3 or 3.98
Come up with a sine function for the graph below.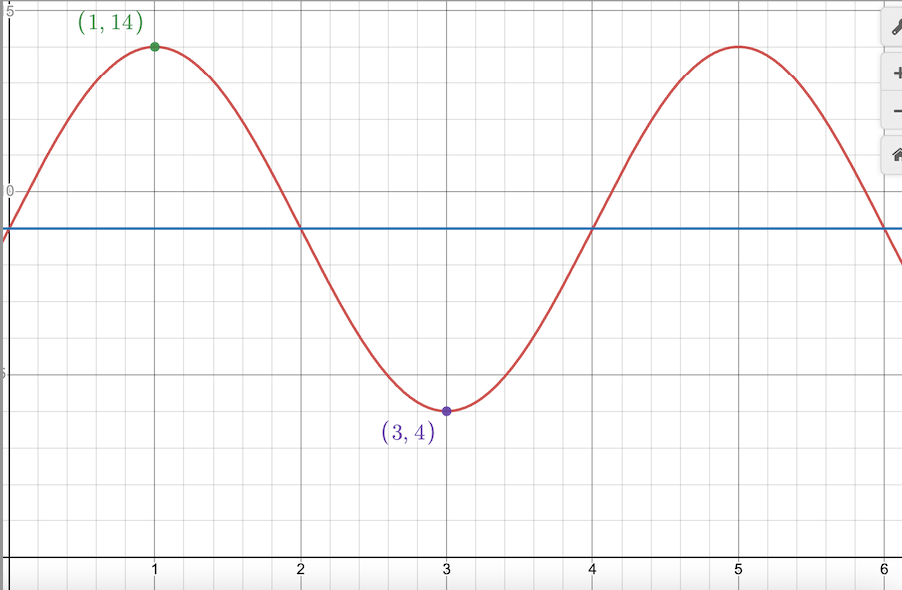
y=5sin(pi/2x)+9
Given
(k - 1)x^2 + 2x + (2k - 3)
, where k is a real number, has real distinct roots, find k
1/2<k<2
f(x)=x-2
and
g(x)=ax+b
Given that, find a and b
f(g(2)) = -3 and g(f(1)) = 5,
a=-2, b=3
Let
f(x)=6-ln(x^2+2)
The graph of
f
passes through the point
(p, 4)
, where
p>0
. Find the value of
p
.
sqrt(e^2-2)=2.32
Find the least POSITIVE value of x for which
cos(x/2+pi/3)=sqrt2/2
x=(17pi)/6
Consider a triangle ABC, where AC=12, CB=7, and angle CAB = 25 degrees. Find the smallest possible perimeter of triangle ABC.
25.1 units.