Is it a function?
no
what notation is this?
{x|x>7 OR x < -2}
set builder notation
Absolute maximum
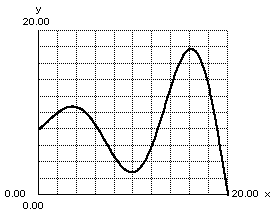
y = 18 (at x = 16)
evaluate the function for f(-5)
f(-5) = -5 + 19 = 14
f(x) = 3x2 - 9x + 14 and g(x) = 12x - 18. Find f+g AND the domain of f+g
f+g = 3x2 + 3x - 4
Domain: all real numbers
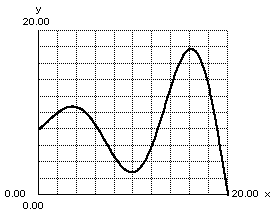
Is it a one-to-one function?
no. it fails the horizontal line test
rewrite in interval notation
-7 <=x or x <-10
(-oo,-10)uu[-7,oo)
constant interval
none
evaluate the function for f(-2)
f(-2) = (-2)3 / (-2 + 9) = -8/7
f(x) = 3x2 - 9x + 14 and g(x) =
-1/x + 7
. Find f-g AND the domain of f-g
f-g = 3x^2 - 9x + 7 +1/x
Domain: x cannot be equal to 0
Is the function even, odd, or neither?

odd
why can this not be written in roster notation?
(-5,3]
because roster notation requires that you list EVERY number in the set. You cannot write all real numbers from -5 (excluded) to 3 (included) in a list
decreasing intervals in interval notation
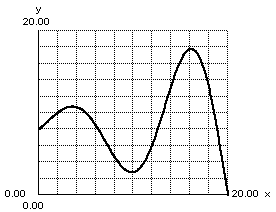
(4,10), (16,20)
Find the range of the graph using interval notation
[-3, oo)
f(x) =
sqrt(2x+5)
and g(x) =
1/x
. Find fg AND the domain of fg
fg =
sqrt(2x+5)/x
Domain of fg
x>=-5/2, x !=0
Does the function have an inverse function?

yes. it is a 1-1 function

What is the independent variable in this situation? What is the dependent variable?
independent variable: time (seconds) after ball is thrown
dependent variable: ball's height (feet)
zeros
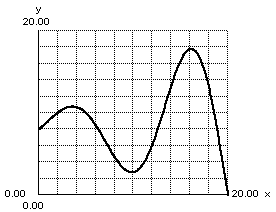
(20,0)
give the domain for each section of the graph using inequalities
x < -1 (left part; constant part)
x
>=
-1 (curved part, right part)
f(x) = 3x - 27 and g(x) = 9x + 18 . Find f/g AND the domain of f/g
f/g =
(x-9)/(3x+6
Domain of f/g:
x!=-2
Give the symmetries of the equation: 3x2y4 - 3xy3 = 19
symmetric to the origin only

Find the height of the ball after 2 seconds
s(2) = 144
After 2 seconds, the ball was 144 feet in the air.
domain, range, and absolute minimum
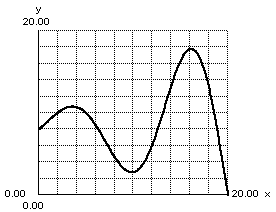
Domain: [0,20]
Range: [0,18]
Absolute Minimum: y = 0 (at x = 20)
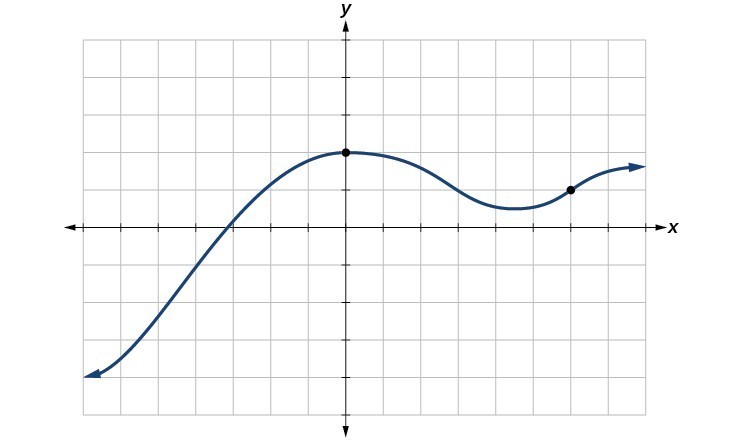
Graph the function and give its range
f(x) = 3x + 4 and g(x) = x2 - 2 . find g(f(x)) AND the domain of g(f(x))
g(f(x)) = 9x2 + 24x + 14
Domain of g(f(x)) = all real numbers