l'Hospital's
Antiderivatives
Optimization
Curve Sketching
Misc
300
lim_(x->0) (x - sinx)/(x - tanx)
-1/2
300
Find the general antiderivative:
f(x) = 5/x^2 - 2/x + 3x^3 - 2sqrtx
F(x) = -5/x - 2lnabs(x) + 3/4x^4 - 4/3x^(3/2) + C
300
Find the point on the curve
y = sqrtx
that is closest to the point (3, 0). Provide an exact coordinate.
(5/2, sqrt(5/2))
300
Find the coordinates of any relative extrema and/or points of inflection of the function. Make sure to label if the extrema is a max or min. Please provide exact coordinates (no decimals)
y = 1 + 1/x + 1/(x^2)
local min:
(-2, 3/4)
POI:
(-3, 7/9)
300
Consider the graph below, which represents f'(x). At which x-value(s) does f(x) have an absolute maximum over the interval [0,4]?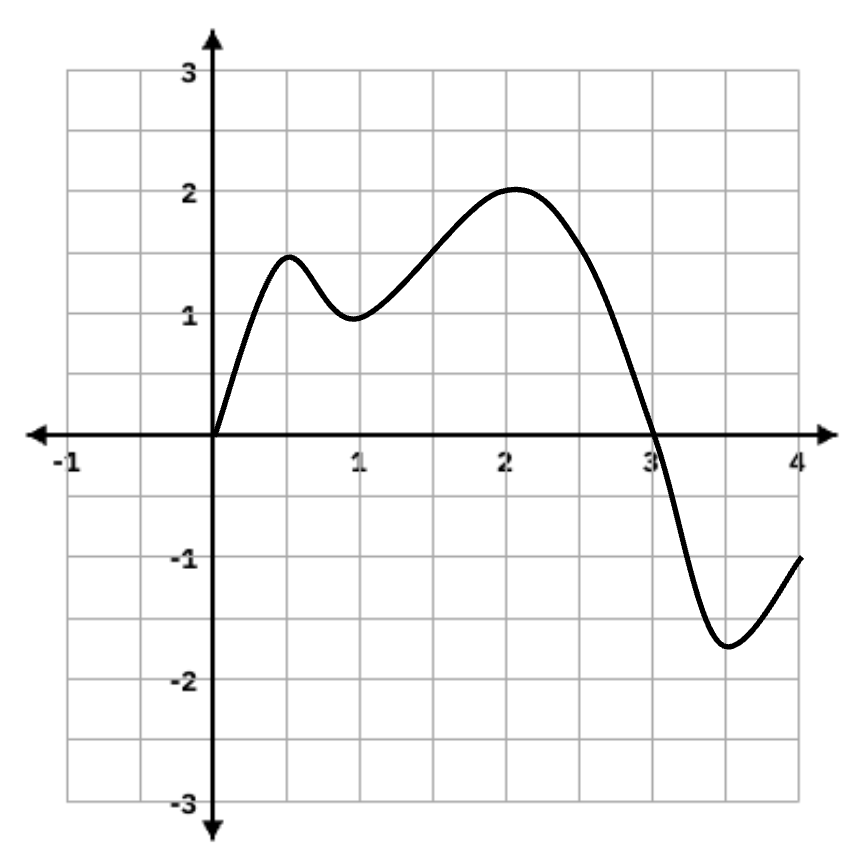
x = 3
400
lim_(x->1) (x/(x - 1) - 1/lnx)
1/2
400
Find the constant of integration for the function if F(0) = 2
f(x) = 2x^3 + 3secxtanx + 1/(sqrt(1-x^2)
C = -1
400
The top and bottom margins of a poster are each 6 cm and the side margins are each 4 cm. If the area of printed material (margins not included) on the poster is fixed at 384 square centimeters, find the dimensions of the entire poster (margins included) with the smallest total area.
24 cm x 36 cm
400
Find the coordinates of any relative extrema and/or points of inflection of the function. Make sure to label if the extrema is a max or min. Please provide exact coordinates (no decimals)
f(x) = x^(5/3) - 5x^(2/3)
Local Max: (0, 0)
Local Min:
(2, -3root(3)4)
POI: (-1, -6)
400
The graph below represents f''(x). If f'(x) = 0 when x=1 and x = 7/2 identify the x-values of the local extrema (if they exist) over the interval [0, 4]. Make sure to clarify if they are a max or min and justify your answer!
Local max at x = 7/2, 2nd derivative test, f''(x)<0
Local min at x = 1, 2nd derivative test, f''(x)>0
500
Evaluate:
lim_(x->oo) x^(ln2/(1 + lnx))
2
500
Find f(x) if f(0)=2 and f(1) = 2 and
f''(x) = root(3)x - cosx
f(x) = 9/28x^(7/3) +cosx + (19/28 - cos1)x + 1
500
A box with an open top is to be constructed from a square piece of cardboard, 3 feet wide, by cutting out a square from each of the four corners and bending up the sides. Find the side length of the square that you should cut out to achieve the largest volume. Then, find the maximum volume. Don't forget units!
1/2 ft, 2 cubic ft
500
Find the coordinates of any relative extrema and/or points of inflection of the function over the given interval. Make sure to label if the extrema is a max or min. Please provide exact coordinates (no decimals)
y = 2x - tanx
-pi/2 < x < pi/2
local max:
(pi/4, pi/2 - 1)
local min:
(-pi/4, -pi/2 + 1)
POI: (0, 0)
500
Find the c value(s) that satisfy MVT for the following function over the interval [2, 5]. Please provide and exact, simplified answer.
f(x) = 4x^3 - 8x^2 + 7x - 2
c = (2 + sqrt79)/3