Graphing Absolute
Value Functions
Value Functions
Solving Absolute Value Equations
Solving Absolute Value Inequalities
Absolute Value Transformations
Vocabulary
Word problems
100
Identify the vertex and slope of the following function and graph it.
y= |x-3|+4
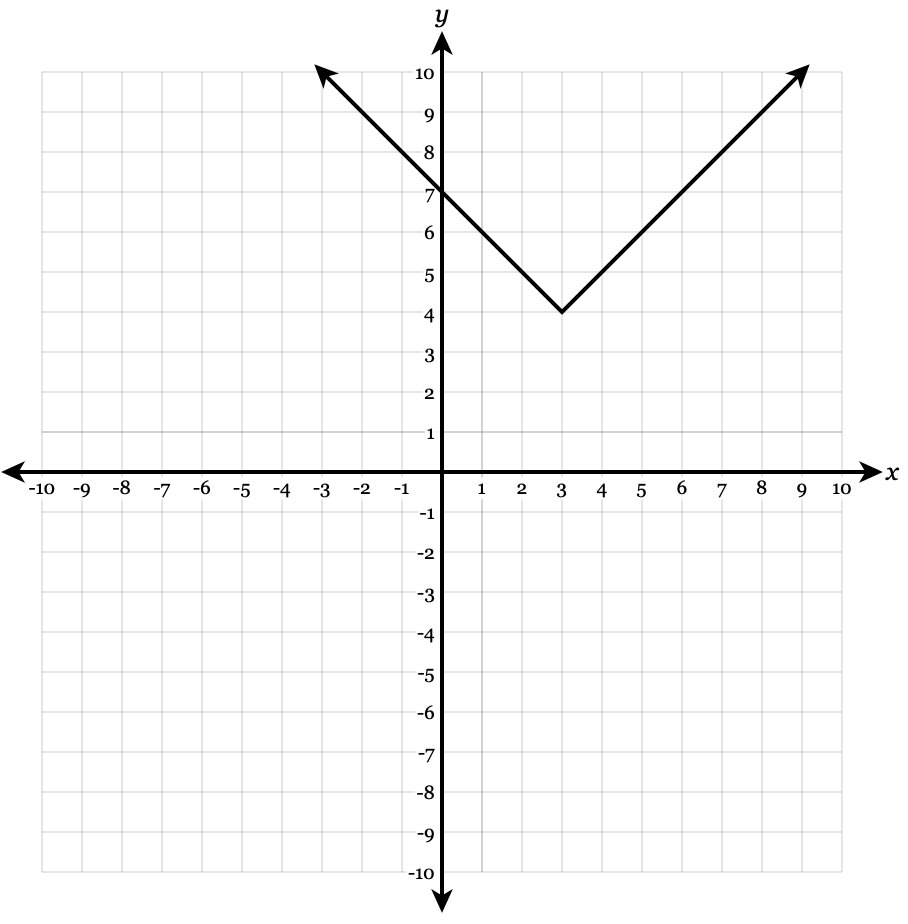
Vertex : (3,4). Slope: 1
100
Solve the absolute value equation ALGEBRAICALLY
-5|x-10|-15=0
-5 |x - 10| - 15 = 0
+ 15 +15
-5 | x - 10| = 15
(-5|x-10|)/-5= 15/-5
|x-10| = -3
No Solution
100
Solve the absolute value inequality by GRAPHING
|x-2|+3<7
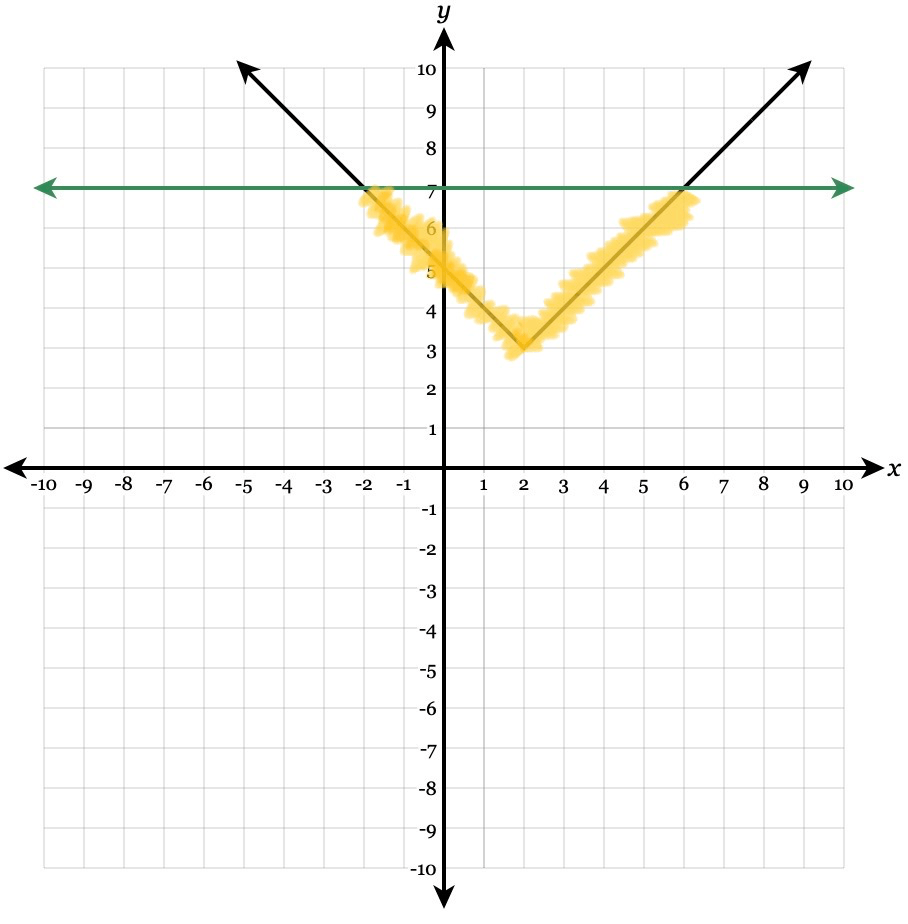-2 < x< 6
100
Identify all the transformations for the absolute value function.
y = |x| - 4
Translates down 4 units
100
What is slope?
Rise over Run
100
John is looking for a job after graduation. The salary which he is satisfied with must be $2500 with a tolerance of $375. Write an inequality that can be used to assess if his salary is tolerable.
|x-2500|<_375
200
Identify the vertex and slope of the following function and graph it.
y=-|x-4|+1
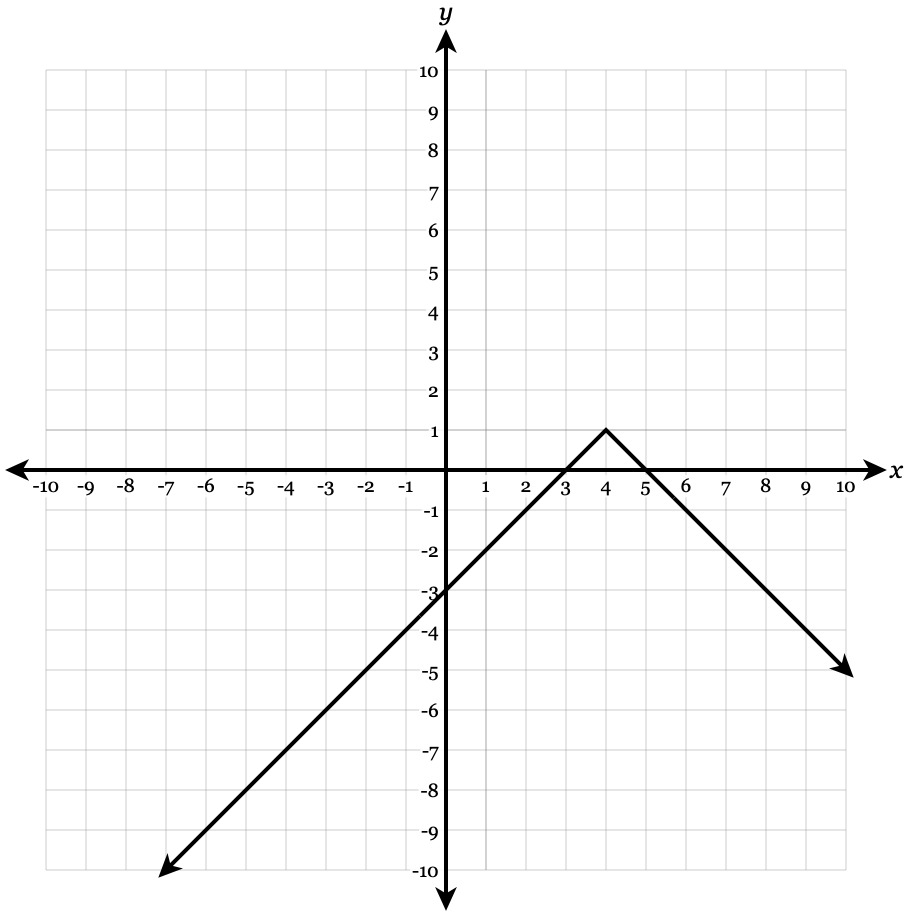
Vertex: (4,1). Slope: -1
200
Solve the absolute value equation by GRAPHING
|x+1|-4=1
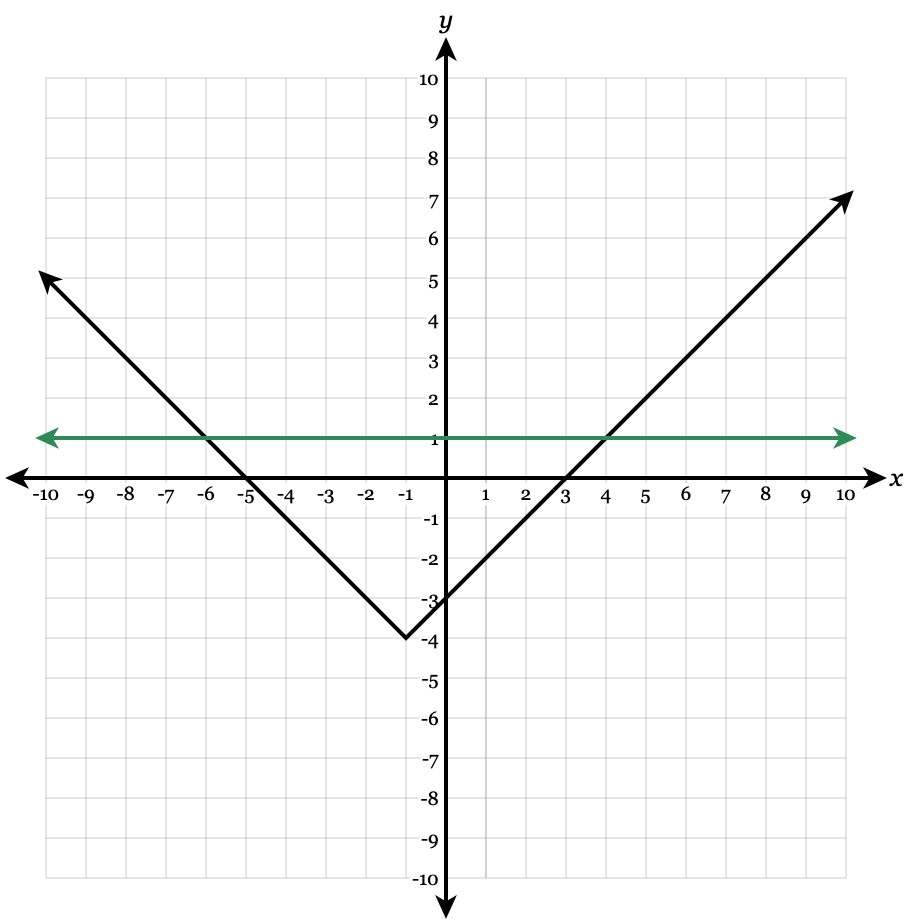
x=-6 and x=4
200
Solve the absolute value inequality ALGEBRAICALLY
|x+4|-22 > -18
|x + 4| - 22 > - 18
+ 22 + 22
|x + 4| > 4
x + 4 > 4 x + 4 < - 4
- 4 - 4 - 4 - 4
x > 0 or x < -8
200
Identify all the transformations for the absolute value function.
y = |x + 2| + 10
1. Translates left 2 units
2. Translates up 10 units
200
What is a y-intercept?
Where the line crosses the y-axis
200
A business meeting will be held at 2:00pm and the doors will be open from 1:45pm to 2:15pm. Write an inequality to assess if an employee will be allowed to enter given that t is the time in hours after 12pm when he or she arrives.
|x-2|<_.25
300
Identify the vertex and slope of the following function and graph it.
y=2|x+5|-3
Vertex: (-5,-3). Slope: 2
300
Solve the absolute value equation by GRAPHING
-3|x+3|+3=-3
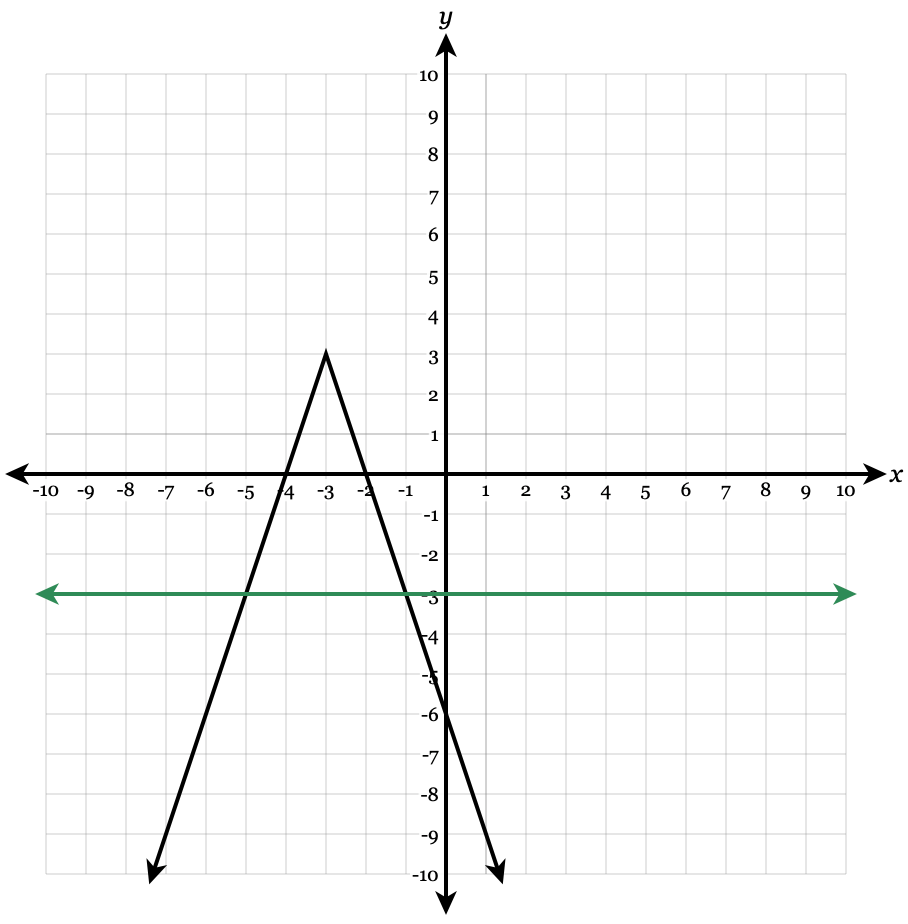
x = -5 and x = -1
300
Solve the absolute value inequality by GRAPHING
2|x+3|-3>=5
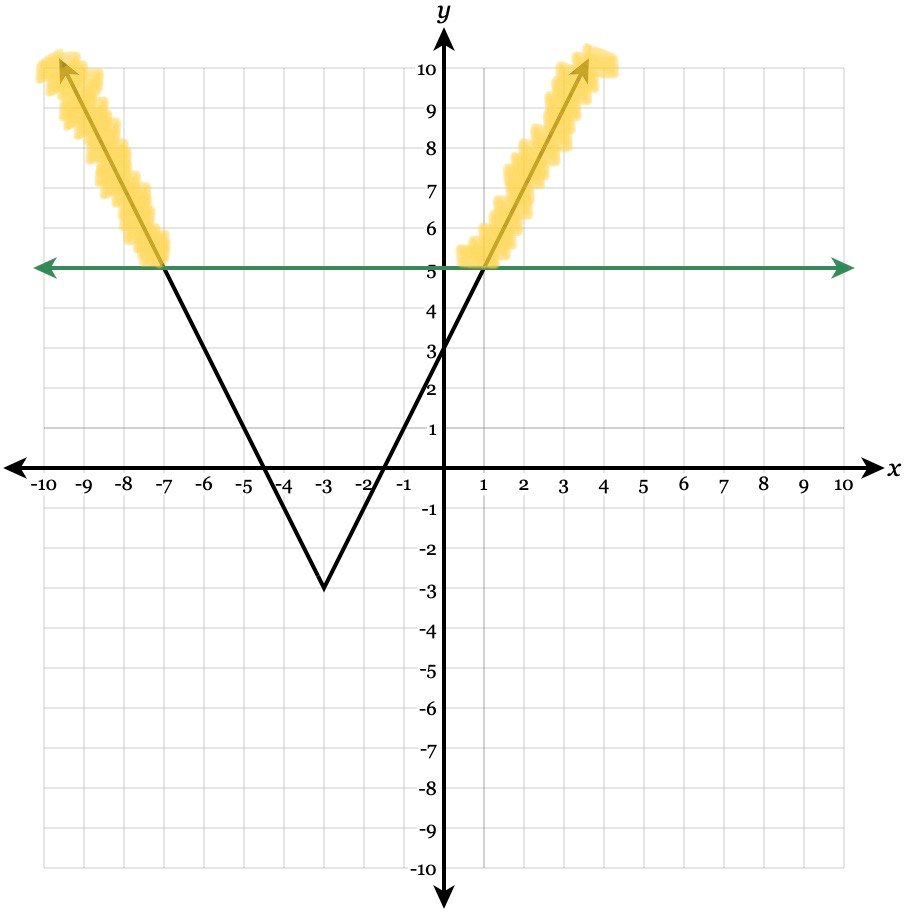
x <=-7 or x>=1
300
Identify all the transformations for the absolute value function.
y= - 1/2| x - 5| + 8
1. Reflects over x-axis
2. Vertical Compression by a factor of 1/2
3. Translates right 5 units
4. Translates up 8 units
300
Define Vertex
Point on a graph where the graph changes direction!
Turning Point
Max/Min
300
The street built in the city must be 27 feet in width with a tolerance of 0.5 feet. Streets that are not within the tolerated widths must be repaired. Write an inequality to assess which streets are within tolerance.
|x-27|<_.5
400
Identify the vertex and slope of the following function and graph it.
y= 3|x+2|-5
Vertex: (-2,-5) Slope: 3
400
Solve the absolute value equation ALGEBRAICALLY
2|x-12|+5 = 15
2|x-12|+5 = 15
-5 -5
2|x-12| = 10
(2|x-12|)/2=10/2
x-12 = 5 x-12 = -5
+12 +12 +12 +12
x = 17 and x = 7
400
Solve the absolute value inequality ALGEBRAICALLY
5|7x-7|+8<=43
5|7x-7|+ 8 ≤ 43
- 8 - 8
5|7x-7|≤ 35
(5|7x-7|)/5 <= (35)/5
|7x-7| ≤ 7
7x - 7 ≤ 7 7x - 7 ≥ -7
+ 7 +7 + 7 +7
7x ≤ 14 7x ≥ 0
(7x)/7 <= 14/7 (7x)/7 >= (0)/2
x<= 2 x>= 0
0<= x <= 2
400
Identify all the transformations for the absolute value function.
y = 3 | -(x + 3)| - 2
1. Vertical stretch by a factor of 3
2. Reflects over y-axis
3. Translates left 3 units
4. Translates down 2 units
400
Define Axis of Symmetry
vertical line going through the vertex
Turning Point of a graph
400
The largest egg of any bird is that of an ostrich. An ostrich egg can reach 8 inches in length. The smallest egg is that of a hummingbird. Its eggs are approximately .4 inches in length. Write an inequality that represents the range of lengths of bird eggs.
.4<_x<_8
500
Identify the vertex and slope of the following function and graph it.
y=-2|x-2|+4
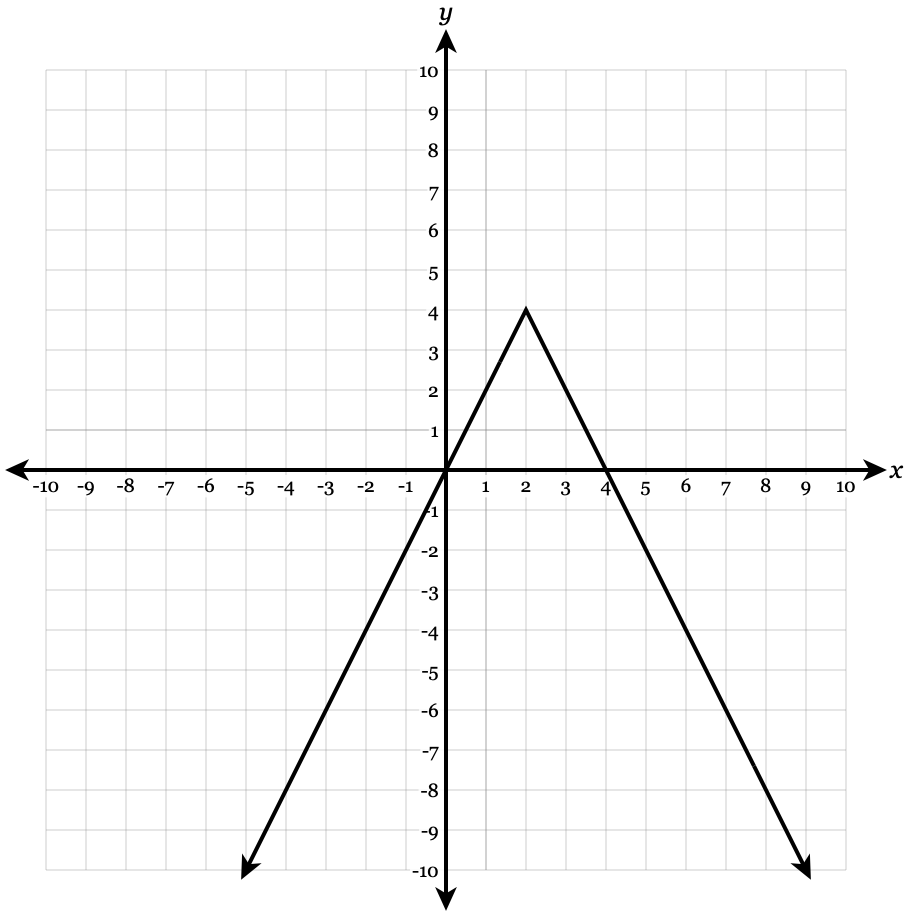
Vertex: (2,4). Slope: -2
500
Solve the absolute value equation ALGEBRAICALLY
4-5|10-5x|=-51
Work will be on the board
x=-1/5 and x= 21/5
500
Solve the absolute value inequality ALGEBRAICALLY
-3|1+2x|+2> -43
- 3 |1+2x|+ 2 > - 43
- 2 - 2
-3|1+2x| > - 45
(-3|1+2x|)/-3 < (-45)/-3
|1+2x| < 15
1 + 2x < 15 1 + 2x > -15
-1 -1 -1 -1
2x < 14 2x > -16
(2x)/2<14/2 (2x)/2 > (-16)/2
x<7 x> -8
-8<x<7
500
Identify all the transformations for the absolute value function.
y= -5|1/2(x+6)|-11
1. Reflects over x-axis
2. Vertical Stretch by a factor of 5
3. Horizontal Stretch by a factor of 2
4. Translates left 6 units
5. Translates down 11 units
500
Absolute Value Vertex Form & what is your vertex?
y = a|x-h|+k
(h,k)
500
On Pennsylvania's interstate highway, the speed limit is 55 mph. The minimum speed limit is 45 mph. Write a compound inequality to represent the allowable speeds.
What is 45<_x<_55