Graphing Absolute
Value Functions
Value Functions
Solving Absolute Value Equations
Solving Absolute Value Inequalities
Absolute Value Transformations
inequalities
100
Graph it.
y= |x-3|+4
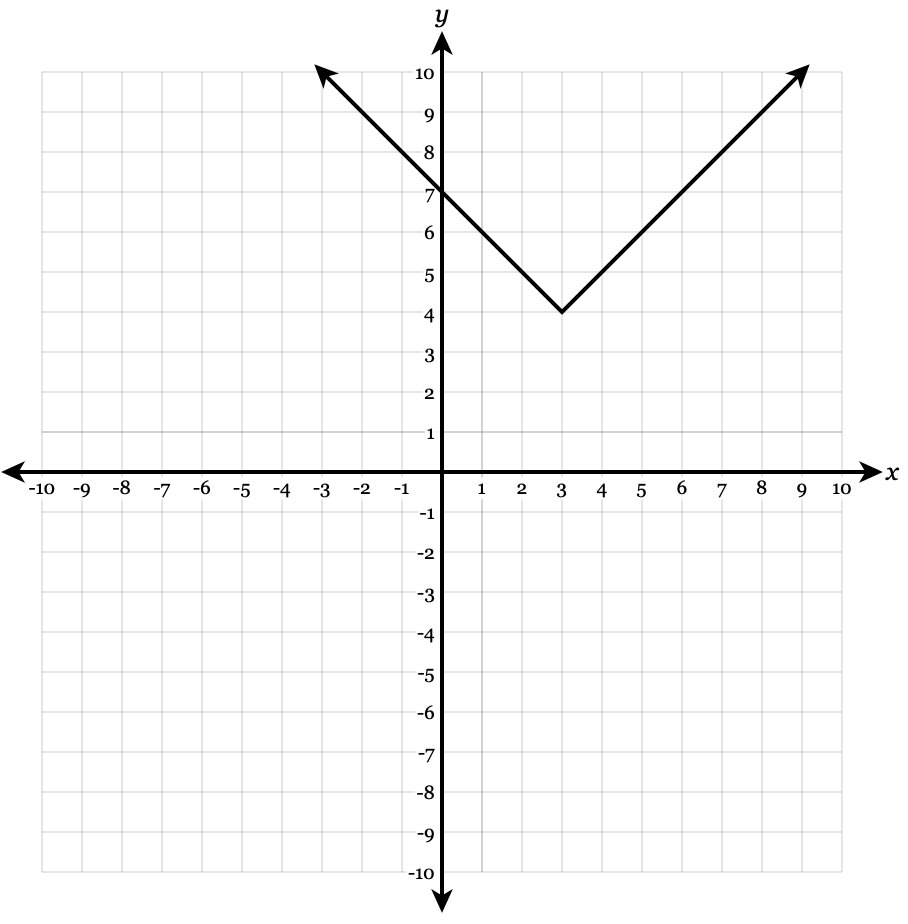
Vertex : (3,4). Slope: 1
100
Solve the absolute value equation ALGEBRAICALLY
-5|x-10|-15=0
No Solution
100
Solve the absolute value inequality by GRAPHING
|x-2|+3<7
-2 < x< 6
(-2,6)
100
Identify all the transformations for the absolute value function.
y = |x| - 4
Translates down 4 units
100
k / 7 > 1 or
-7 + k <= -10
k > 7 or k <= -3
(-\infty,-3]U(7,\infty)
200
Graph it.
y=-|x-4|+1
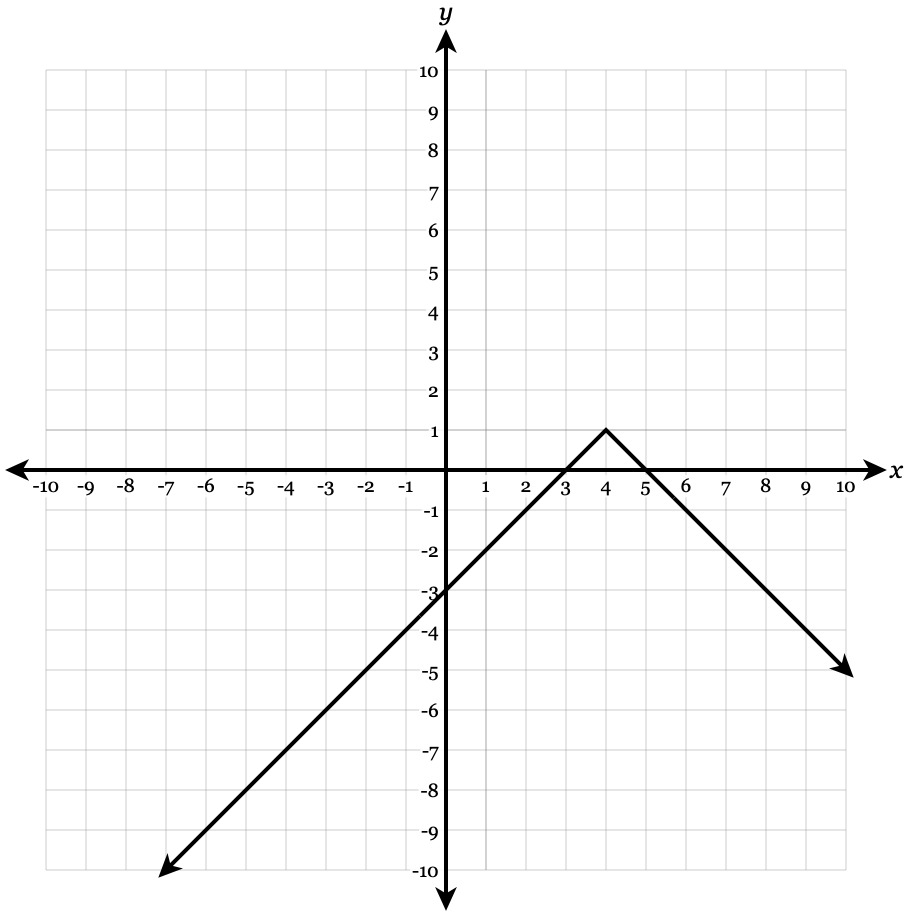
Vertex: (4,1). Slope: -1
200
Solve the absolute value equation by GRAPHING
|x+1|-4=1
x=-6 and x=4
200
Solve the absolute value inequality ALGEBRAICALLY
|x+4|-22 > -18
x > 0 or x < -8
(\-infty,-8)U(0,\infty)
200
Identify all the transformations for the absolute value function.
y = |x + 2| + 10
1. Translates left 2 units
2. Translates up 10 units
200
-1 < x / 7 < 0
-7 < x < 0
300
Graph it.
y=2|x+5|-3
Vertex: (-5,-3). Slope: 2
300
Solve the absolute value equation by GRAPHING
-3|x+3|+3=-3
x = -5 and x = -1
300
Solve the absolute value inequality by GRAPHING
2|x+3|-3>=5
x <=-7 or x>=1
(-\infty,-7)U(1,\infty)
300
Identify all the transformations for the absolute value function.
y= - 1/2| x - 5| + 8
1. Reflects over x-axis
2. Vertical Compression by a factor of 1/2
3. Translates right 5 units
4. Translates up 8 units
300
4x + 7 >= 27
or
9 + 2x <= 3
x >= 5 or x <= -3
(\-infty,,-3]U[5,\infty)
400
Graph it.
y= 3|x+2|-5
Vertex: (-2,-5) Slope: 3
400
Solve the absolute value equation ALGEBRAICALLY
2|x-12|+5 = 15
x = 17 and x = 7
400
Solve the absolute value inequality ALGEBRAICALLY
5|7x-7|+8<=43
0<= x <= 2
[0,2]
400
Identify all the transformations for the absolute value function.
y = 3 | -(x + 3)| - 2
1. Vertical stretch by a factor of 3
2. Reflects over y-axis
3. Translates left 3 units
4. Translates down 2 units
400
-32 <= 3 + 7k < 73
-5 <= k < 10
[-5,10)
500
Graph it.
y=-2|x-2|+4
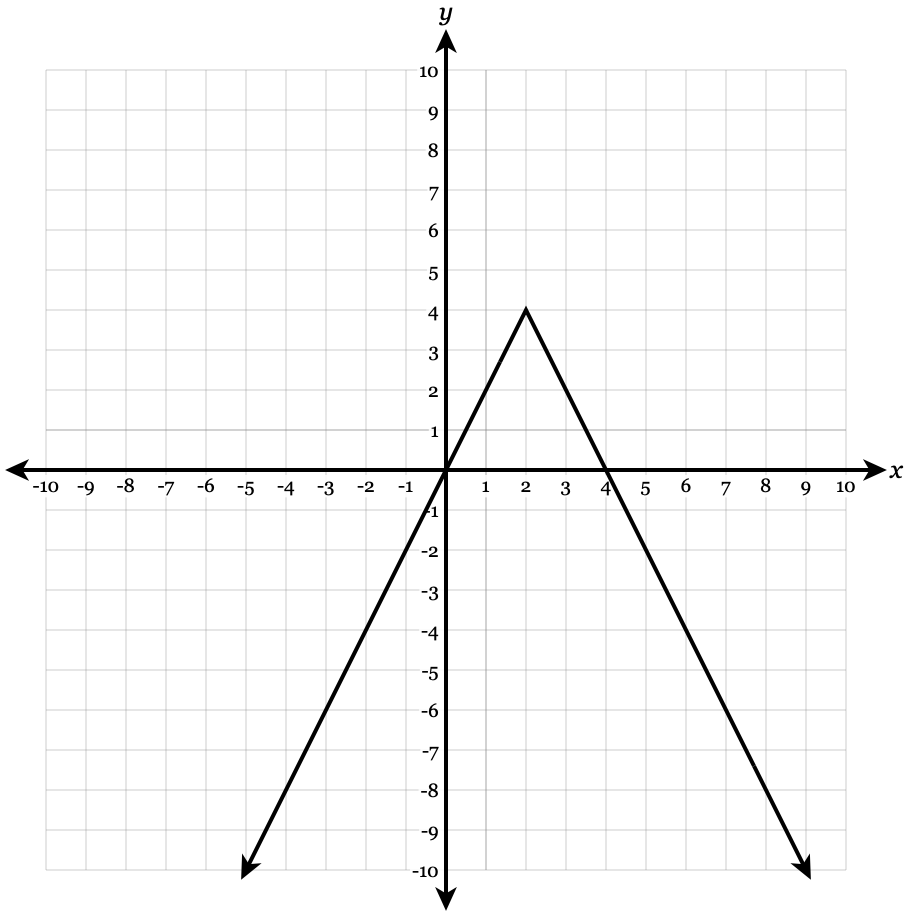
Vertex: (2,4). Slope: -2
500
Solve the absolute value equation ALGEBRAICALLY
4-5|10-5x|=-51
x=-1/5 and x= 21/5
500
Solve the absolute value inequality ALGEBRAICALLY
-3|1+2x|+2> -43
-8<x<7
(-8,7)
500
Identify all the transformations for the absolute value function.
y= -5|1/2(x+6)|-11
1. Reflects over x-axis
2. Vertical Stretch by a factor of 5
3. Horizontal Stretch by a factor of 2
4. Translates left 6 units
5. Translates down 11 units
500
3x - 8 >= 4 - 3x
or
4x - 7 >= 9 + 8x
x >= 2 or x <= -4
(-\infty, -4]U[2,\infty)