Up or Down
What shape is the graph of an absolute value function?
a V
Give the y-intercept of the quadratic function
3
Will the parabola open up or down?
x^2 - 4x - 1
up
Find the vertex: |x| -1
(0, -1)
Given x = -1
f(x) =
-x^2 - 3x + 2
f(x) = 4
What shape is the graph of a quadratic function?
a parabola (U)
Give the roots of the parabola
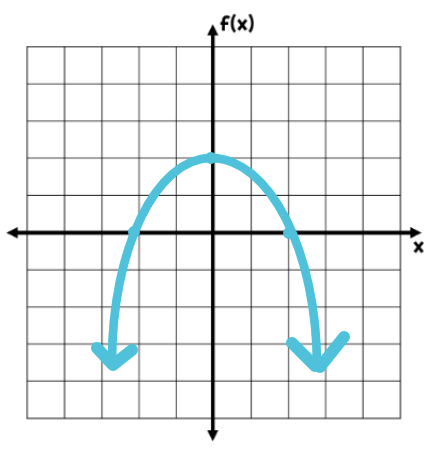
{-2, 2}
Will the parabola have a minimum or a maximum as its vertex?
x^2 - 4x - 1
minimum
Will the graph open up or down?
-|x + 1| + 3
down (negative outside the bars)
Given x = 4
f(x) =
x^2 - 2x - 3
f(x) = 5
Where can you find the y-intercept on each graph?
It is where the graph hits the y-axis
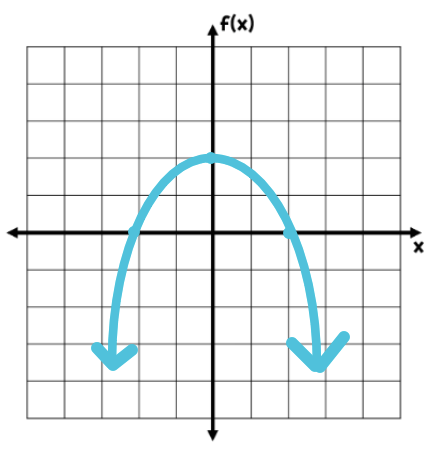
What do you know about the leading coefficient based on this parabola?
It is negative
Will the parabola open up or down?
-3x^2 + 2x + 5
down
Find the vertex: |x - 4| + 2
(4, 2)
Given x = -5
f(x) =
-|x + 1| - 2
f(x) = -6
Where do you find the roots of a quadratic function?
Where the parabola crosses the x-axis
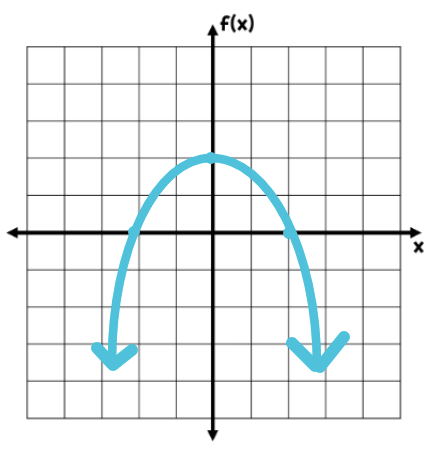
What is the axis of symmetry for the parabola shown:
x = 3
Will the parabola have a minimum or a maximum?
1/2x^2 + 2x - 8
minimum
Find the vertex: f(x) = |2x + 4|+ 3
(-2, 3)
Given x = 4
f(x) =
1/2x^2 + 3
f(x) = 11
How do you find the axis of symmetry for the parabola?
It is the line that goes through the vertex
It is always x = (the x-coordinate of the vertex)
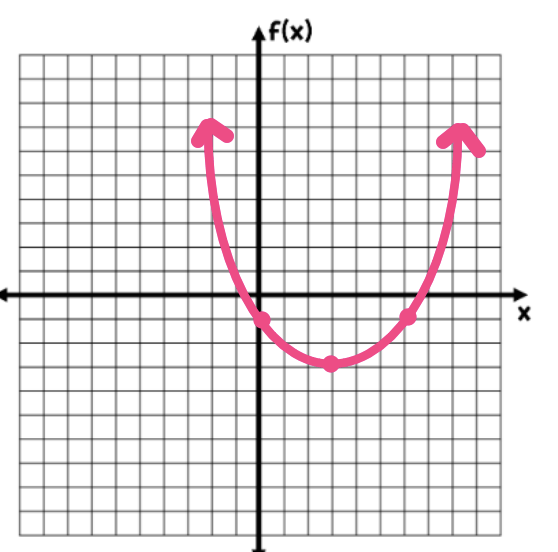
What are the roots of the parabola?
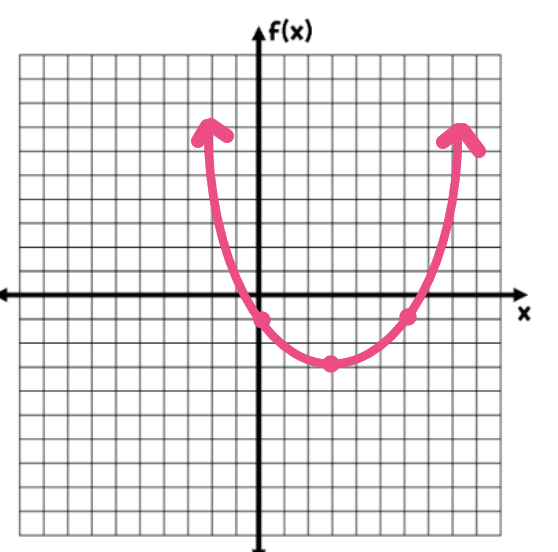
{-1, 7}
From an equation, how can you tell if the parabola will open up or down?
By the leading coefficient: if it is positive the parabola will open up and if it is negative the parabola will open down
Give the absolute value function based on the graph:
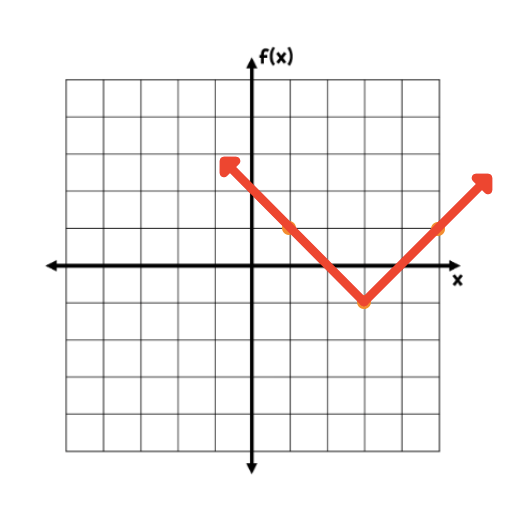
f(x) = |x - 3| - 1
Given x = 6
f(x) =
-1/3x^2 - 2x + 1
f(x) = -23