What is the degree measure of the acute angle formed by the hands of a 12-hour clock that reads exactly 1 o’clock?
A. 15 degrees
B. 30 degrees
C. 45 degrees
D. 60 degrees
E. 72 degrees
B. 30 degrees
One complete rotation of a clock hand is 360°, and there are 12 hourly markings on a clock. When the hands read exactly 1 o'clock, the degree measure of the angle formed by the clock hands is 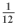 of a complete rotation, or
of a complete rotation, or 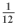 (360°) = 30°.
(360°) = 30°.
What is the probability that a number selected at random from the set {2, 3, 7, 12, 15, 22, 72, 108} will be divisible by both 2 and 3 ?
F. 1/4
G. 3/8
H. 3/5
I. 5/8
J. 7/8
G. 3/8
Since 12, 72, and 108 are the only numbers in the list divisible by both 2 and 3, the probability that the number selected at random is divisible by both 2 and 3 is ⅜
A circle has a circumference of 16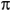 feet. What is the radius of the circle, in feet?
feet. What is the radius of the circle, in feet?
A. 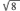
B. 4
C. 8
D. 16
E. 32
C. 8
The formula for the circumference of a circle with radius r is 2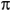 r. So 2
r. So 2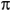 r= 16 , or r = 8.
r= 16 , or r = 8.
A rectangle with a perimeter of 30 centimeters is twice as long as it is wide. What is the area of the rectangle in square centimeters?
F. 15
G. 50
H. 200
I. 3^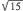
J. 6^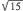
G. 50
If w = width, then 2w = length. So, the perimeter is 2(w + 2w) = 30, and w = 5. Since the width is 5, the length is 2(5) = 10. Then the area is 5(10) = 50.
In the standard (x,y)coordinate plane, what are the coordinates of the midpoint of a line segment whose endpoints are (–3,0) and (7,4) ?
A. (2,2)
B. (2,4)
C. (5,2)
D. (5,4)
E. (5,5)
A. (2,2)
To find the midpoint, you need to take the average of each of the coordinates, 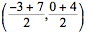 = (2,2).
= (2,2).
Points A, B, C, and D are on a line such that B is between A and C, and C is between B and D. The distance from A to B is 6 units. The distance from B to C is twice the distance from A to B, and the distance from C to D is twice the distance from B to C. What is the distance, in units, from the midpoint of 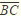 to the midpoint of
to the midpoint of 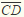 ?
?
F. 18
G. 14
H. 12
I. 9
J. 6
F. 18
BC = 2AB = 2(6) = 12 and CD = 2BC = 2(12) = 24. The distance between the midpoints of BC and CD is 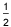 BC +
BC + 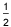 CD =
CD = 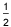 (12)+
(12)+ 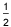 (24) = 18
(24) = 18
Which of the following statements must be true whenever n, a, b, and c are positive integers such that
n < a, c > a, and b > c ?
A. a < n
B. b-n > a-n
C. b < n
D. n+b = a+c
E. 2n > a+b
B. b-n > a-n
Since b > a, subtracting n from each side, b – n > a – n, will not change the relationship between b and a.
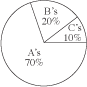
The distribution of Jamal’s high school grades by percentage of course credits is given in the circle graph below. What is Jamal’s grade point average if each A is worth 4 points; each B, 3 points; and each C, 2 points?
F. 3.0
G. 3.4
H. 3.6
I. 3.7
J. Cannot be determined from the given information
H. 3.6
This is the correct answer since 4(0.7) + 3(0.2) + 2(0.1) = 3.6.

What is the difference between 1.8 and 1.080808080...?
A. 0.7111...
B. 0.717171...
C. 0.7191919...
D. 0.7222...
E. 0.727272...
C. 0.7191919...
Take 1.080808... and repeat the pattern several times, then subtract that from 1.8. 1.8 – 1.08080808 ≈ 0.7191919. Realizing that the pattern should repeat, you can conclude that 0.7191919... is the correct answer.
Which of the following equations represents the linear relationship between time, t, and velocity, v, shown in the table below?
t|0|1|2
v|120|152|184
F. v = 32t
G. v = 32t +120
H. v = 120t
I. v = 120t + 32
J. v = 120t +120
G. v = 32t + 120
A linear relationship means the associated graph is a line. So, you can think of the ordered pairs (t,v) as points on the line. Since (0,120), (1,152), and (2,184) are points on the line, the slope of the line is 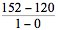 = 32. Therefore, v = 32t + b, where b is the y-intercept of the line. Since (0,120) is a point on the line, 120 = 32(0) + b, or b = 120. Thus, an equation for the line is v = 32t + 120.
= 32. Therefore, v = 32t + b, where b is the y-intercept of the line. Since (0,120) is a point on the line, 120 = 32(0) + b, or b = 120. Thus, an equation for the line is v = 32t + 120.
An industrial cleaner is manufactured using only the 3 secret ingredients A, B, and C, which are mixed in the ratio of 2:3:5, respectively, by weight. How many pounds of secret ingredient B are in a 42-pound (net weight) bucket of this cleaner?
A. 4.2
B. 12.6
C. 14.0
D. 18.0
E. 21.0
B. 12.6
If you let 3x be amount of secret ingredient B, you can set up the equation 2x + 3x + 5x = 42. Since 10x = 42, x = 4.2, and B = 3x = 12.6.
If n = 8 and 16 • 2m = 4n – 8, then m = ?
F. -4
G. -2
H. 0
I. 1
J. 8
F. -4
When n = 8, 4n – 8 = 48 – 8 = 40 = 1,
and 16 · 2m = 24 · 2m = 24 + m.
So, 24 + m= 1, and any number to the zeroth power is 1, so 4 + m = 0, or m = –4.
In the figure below, A, B, C, and D are collinear, FC is parallel to ED, BE is perpendicular to ED, and the measures of ∠FAB and ∠EBA are as marked. What is the measure of ∠FCB ?
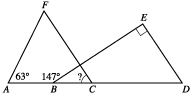
A. 33 degrees
B. 57 degrees
C. 63 degrees
D. 84 degrees
E. Cannot be determined from the given information.
B. 57 degrees
Since FC and ED are two parallel line segments cut by transversal BE, ∠E and ∠BGC are corresponding angles. So, the measure of ∠BGC is 90°. Since ∠ABG ∠GBC are supplementary angles, the measure of ∠GBC = 180° – 147° = 33°. Looking at ΔBGC, the sum of the measures of angles ∠GCB, ∠BGC, and ∠GBC is 180°. So, the measure of ∠GCB + 90° + 33° = 180°, or 180° – 90° – 33° = 57°.

Which of the following is an equation of the circle with its center at (0,0) that passes through (3,4) in the standard (x,y) coordinate plane?
F. x – y = 1
G. x – y = 25
H. x2 + y = 25
I. x2 + y2 = 5
J. x2 + y2 = 25
J. x2 + y2 = 25
The radius of the circle is the distance between (0,0) and (3,4), which is √((3–0)2+ (4–0)2) = 5. An equation of a circle where (h,k) is the center and r is the radius is (x – h)2 + (y – k)2 = r2. So (x – 0)2 + (y – 0)2 = 52 or x2 + y2 = 25.
Taher has decided to create a triangular flower bed border. He plans to use 3 pieces of rectangular lumber with lengths 4, 5, and 6 feet, as shown in the figure below. Points A, B, and C are located at the corners of the flower bed.

Taher plans to cut the 3 pieces of lumber for the flower bed border from a single piece of lumber. Each cut takes 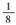 inch of wood off the length of the piece of lumber. Among the following lengths, in inches, of pieces of lumber, which is the shortest piece that he can use to cut the pieces for the flower bed border?
inch of wood off the length of the piece of lumber. Among the following lengths, in inches, of pieces of lumber, which is the shortest piece that he can use to cut the pieces for the flower bed border?
A. 178
B. 179
C. 180
D. 181
E. 182
D. 181
The number of inches of wood needed if there were no cuts is 4 + 5 + 6 = 15 feet, or 180 inches. However, you need to add 2(<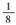 ) for 2 cuts that are needed so that you have lumber for each of the 3 sides. Since 180 + 2(
) for 2 cuts that are needed so that you have lumber for each of the 3 sides. Since 180 + 2(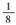 ) = 180 +
) = 180 + 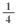 , the minimum piece needed to construct the flower bed border including the 2 cuts would be 181 inches.
, the minimum piece needed to construct the flower bed border including the 2 cuts would be 181 inches.
Which one of the following expressions has an even integer value for all integers a and c ?
F. 8a + 2ac
G. 3a + 3c
H. 2a + c
I. a + 2c
J. ac + a2
F. 8a + 2ac
8a + 2ac is even because it is divisible by 2, 8a + 2ac = 2(4a+ ac), and 4a + ac is an integer because a and c are integers.
A neighborhood recreation program serves a total of 280 children who are either 11 years old or 12 years old. The sum of the children’s ages is 3,238 years. How many 11-year-old children does the recreation program serve?
A. 55
B. 122
C. 132
D. 158
E. 208
B. 122
If you let e = number of 11-year-olds and t = number of 12-year-olds, then you can solve the system e + t = 280 and 11e + 12t = 3,238. Substitution, elimination, and matrices are just some of the methods you could use to solve the system. Just remember, in the end, you want to solve for e.
The geometric figure shown below consists of a square and 4 semicircles. The diameters of the semicircles are the sides of the square, and each diameter is 10 centimeters long. Which of the following is the closest approximation of the total area, in square centimeters, of this geometric figure?
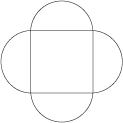
F. 100
G. 160
H. 260
I. 400
J. 730
H. 260
You found the area of the square, the area of 4 semicircles (or the area of 2 full circles), and added them. 102 + 2pi(5)2 ≈ 257. The closest answer is 260.
Which of the following expressions is the closest approximation to the height h, in feet, of the roof truss shown below?
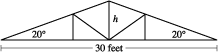
A. 15 tan 20°
B. 15 sin 20°
C. 30 tan 20°
D. 30 sin 20°
E. 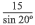
A. 15 tan 20°
YZ = 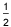 XZ =
XZ = 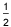 30) = 15.
30) = 15.
So, tan 20° = 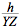 =
= 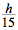 . Then h = 15 tan 20°.
. Then h = 15 tan 20°.

Taher has decided to create a triangular flower bed border. He plans to use 3 pieces of rectangular lumber with lengths 4, 5, and 6 feet, as shown in the figure below. Points A, B, and C are located at the corners of the flower bed.

The measure of ∠ABC in the figure is x°. Which of the following is an expression for β° ?
F. x°
G. 2x°
H. (90 + x)°
I. (180 – x)°
J. (180 – 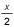 )°
)°
I. (180 – x)°
The angles of the rectangular pieces of lumber measure 90°, so the sum of the measure of the angles at β is 360°. β + 90 + x + 90 = 360, or β = 180 – x.
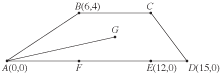
Quadrilateral ABCD is drawn on the standard (x,y) coordinate plane as shown below, with points E and F on AD. Point G is the center of rectangle BCEF. How many coordinate units long is AG ?
F. 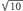
G. 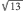
H. 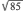
I. 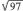
J. 11
H. 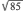
By drawing in rectangle BCEF and diagonal BE, you can find the coordinates of G by finding the midpoint of BE. So G is at 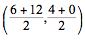 , or (9,2). Using the distance formula, AG = √((9 – 0)2 + (2 – 0)2) = √(81 + 4) = √85.
, or (9,2). Using the distance formula, AG = √((9 – 0)2 + (2 – 0)2) = √(81 + 4) = √85.

What is the x-intercept of the graph of y = x2 – 4x + 4?
A. -2
B. -1
C. 0
D. 1
E. 2
E. 2
One way to find the x-intercept is to replace y with 0 and solve for x. If 0 = x2 – 4x + 4, then (x – 2)2 = 0, and x = 2. Another way of doing this problem is to look at the graph of the equation and see where the graph crosses the x-axis.
For all nonzero real numbers p, t, x, and y such that 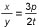 , which of the following expressions is equivalent to t ?
, which of the following expressions is equivalent to t ?
F. 
G. 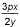
H. 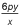
I. 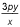
J. 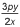
J. 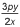
If you cross multiply, 2xt = 3py. Then dividing each side by 2x, you get t = 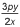 .
.
Which of the following is equivalent to sin θ csc(–θ) wherever sin θ csc(–θ) is defined?
A. -1
B. 1
C. –tanθ
D. tanθ
E. –sin2θ
A. -1
csc(–θ) = –cscθ = – 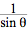 . So, sinθ csc(–θ) = sinθ(–
. So, sinθ csc(–θ) = sinθ(– 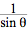 ) = –1 .
) = –1 .
Taher has decided to create a triangular flower bed border. He plans to use 3 pieces of rectangular lumber with lengths 4, 5, and 6 feet, as shown in the figure below. Points A, B, and C are located at the corners of the flower bed.

After arranging the flower bed, Taher decides that the flower bed would look more attractive if 1 of the angles in the triangle were a right angle. He decides to place the right angle at vertex A and to leave the lengths of AB and AC as 4 and 5 feet, respectively. To the nearest 0.1 foot, how long of a piece of lumber would he need to replace the 6-foot piece represented by BC ?
A. 3.0
B. 3.3
C. 6.0
D. 6.4
E. 7.8
D. 6.4
Using the Pythagorean theorem, 42 + 52 = (BC)2. Then BC = √(42 + 52) = √41 ≈ 6.4.