What is the y intercept of the function: h(x)=x^2+6x+8
(0,8)
What is the aos and vertex of the function in vertex form: h(x)=-3(x-1)^2+6
a.o.s: x = 1
Vertex: (1,6)
If the equation of the quadratic is h(x)=x^2+6x+8 , choose the characteristics:
a) up or down
b) normal, wide, or narrow,
c) Maximum or minimum vertex
up, normal, minimum
What function is quadratic?
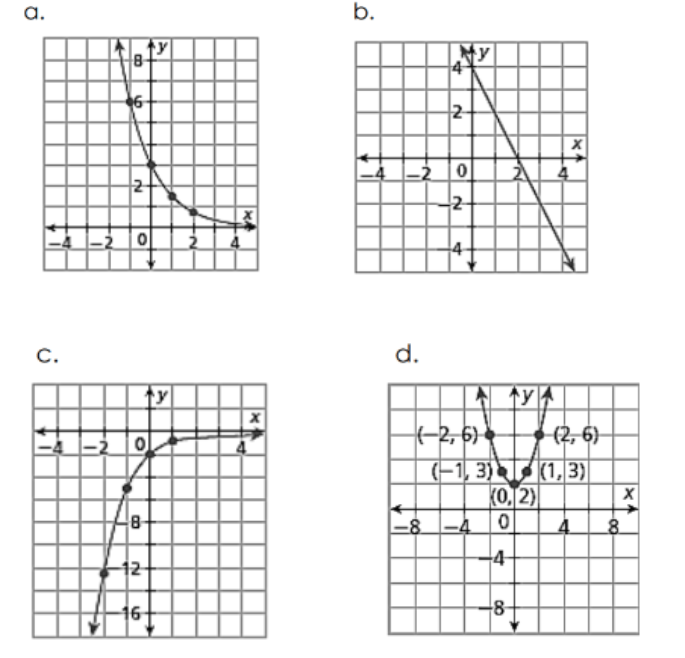
D
Match the equation with the form: which is in simplified standard form and which is in vertex form?
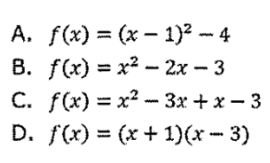
Standard form: B
Vertex form: A
What is the a.o.s of the function: h(x)=x^2+6x+8
x=-3
If the equation of the quadratic is h(x) = -3(x-1)^2+6 , chose the charateristics
a)up or down
b) Normal. wide or narrow
c) maximum or minimum
a) down
b) narrow
c) maximum
If the equation of the quadratic is h(x)=-3(x-1)^2+6 , choose the characteristics:
a) up or down
b) normal, wide, or narrow,
c) Maximum or minimum vertex
a) down
b) narrow
c) maximum
Which table represents Exponential -- and is it growth or decay ? (answer both)
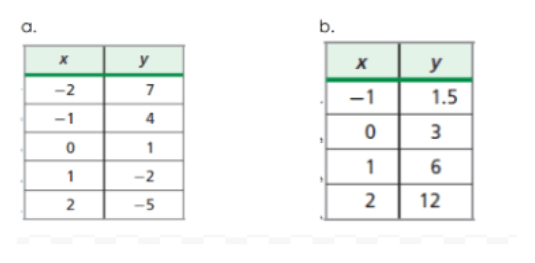
B. Exponential Growth
Write an equation of a function of a quadratic that has a vertex that is translated 2 units horizontally to the right and 4 units up of the vertex of the graph of f(x)=3(x-5)^2+6
f(x)=3(x-7)^2+10
What is the vertex of the function:
h(x)=x^2+6x+8
(-3,-1)
The graph of y=-3(x-1)^2+6 is graphed below. what is the domain and range?
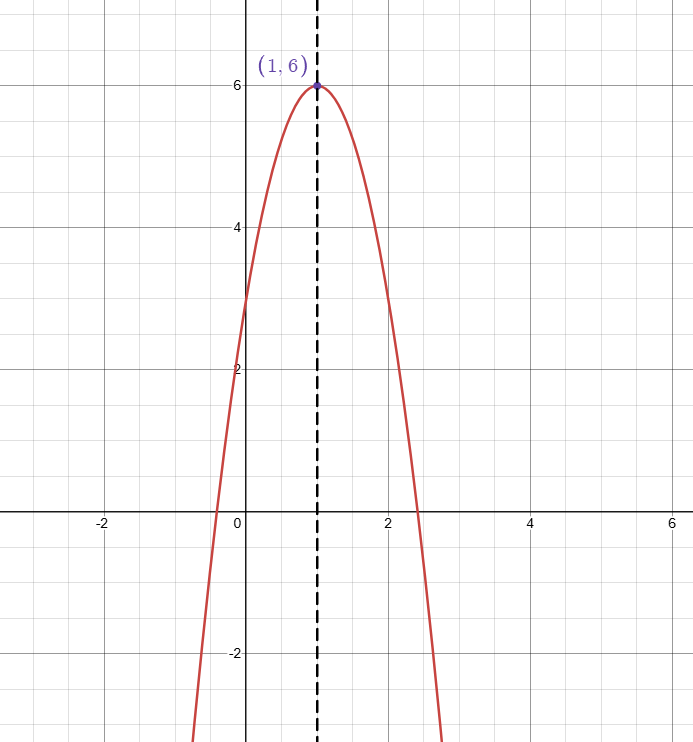
Domain: (-oo,oo) and
Range: (-oo,6]
What are the key features of the function below
g(x)=-2x^2
Opens:
Narrow/Wide/Normal:
Vertex :
A.O.S:
down, narrow, vertex (0,0) aos: x = 0
Which table is quadratic - and is it positive or negative quadratic?
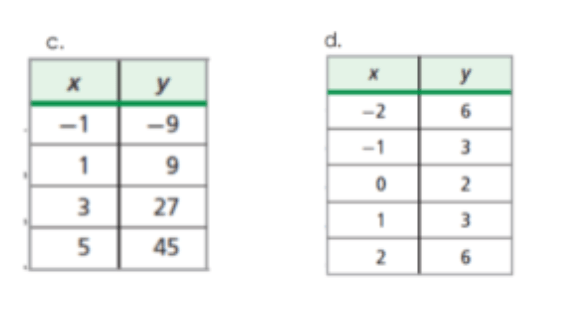
D. Positive Quadratic
An object is launched upward with an initial velocity of 64 feet per second (ft/s) from a platform 80 feet high. Write an equation and find out when will it attain a maximum height?
Use the euqation for feet: h(t)=-16t^2+v_o(t)+h_o
Equation: h(t) = -16t^2+64t+80
Time: at 2 seconds
The quadratic function y=x^2+6x+8 is graphed below.
Over what interval is the function INCREASING ?
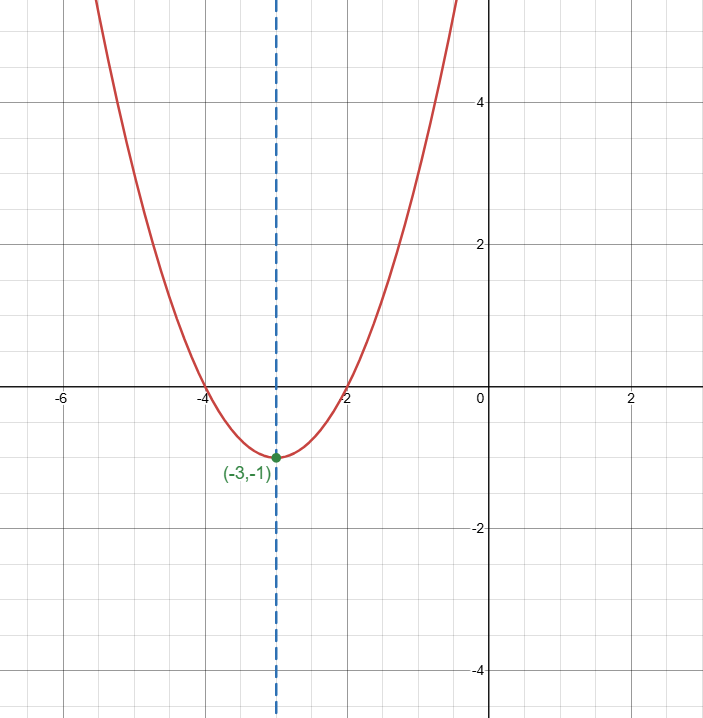
(-3,oo)
Convert the function that is in vertex form to standard form: f(x) = -3(x-1)^2+6
f(x) =-3x^2+6x+3
The graph of h is the graph of f(x)=x^2 translated 4 units left and 7 units down. Write the function h(x) in Vertex Form and in Standard form.
Vertex form: f(x)=(x+4)^2-7
Standard form:
f(x)=x^2+8x+9
Which function best describes the discrete (dotted) graph of the function: f(x)=-x^2+18x
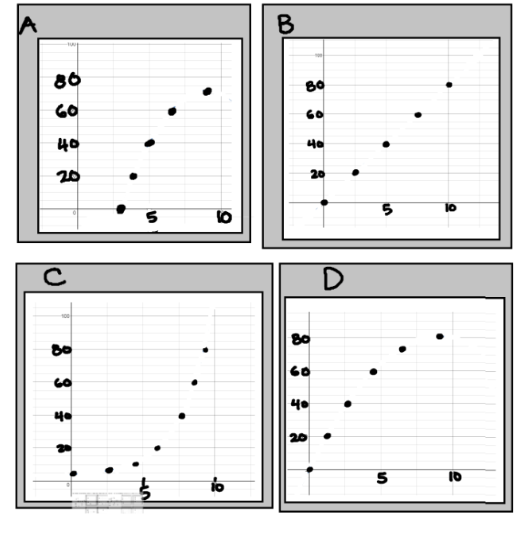
D. Because the y intercept is zero
An object is launched at an initial velocity of 19.6 meters per second from a 58.8-meter tall platform. Write the equation for the Projectile Motion problem and then find out the max height.
Use the meter equation:
h(t)=-4.9t^2+v_o(t)+h_o
h(t)=-4.9t^2+19.6t+58.8
Max Height: 78.4 meters
What is the average rate of change of the function below over the interval: -2<=x<=-1
h(x)=x^2+6x+8
3
What is the y intercept of the equation below
f(x)=-3(x-1)^2+6
(0,3)
What is the average rate of change for g(x)=root3(x+5)+1 over the interval [22,59]
1/37 or 0.027
The graph of the quadratic function below has a vertex of ( -1,4) and points to the left and the right at (-2,3) and (0,3). What is the equation of the quadratic in standard form?
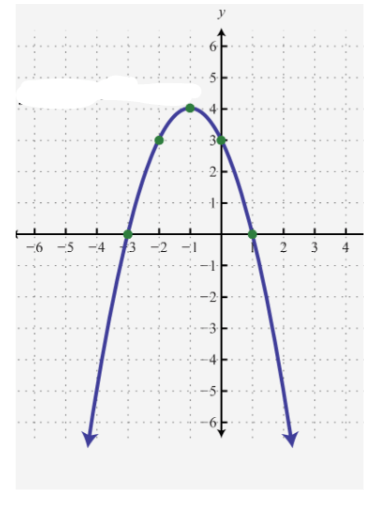
y=-x^2-2x+3
Sara wants to build a pool in her backyard. She would like to build a wood deck around her rectangular pool. The deck she wants is 4 feet wide. She would like the length of her pool to be twice as long as the width. Write an equation (in standard form) modeling the area that is needed in her backyard - and find the area needed if she desires the width to be 10 feet.
2x^2+24x+64
504 ft^2