What are the end behaviours for an odd degree function with a negative leading coefficient?
x-> -\infty , f(x)->\infty
x-> infty , f(x) -> -\infty
Where are the vertical asymptotes for the following function? f(x)=1/(x^2+7x-10
x=-8.217
x=1.217
create an equation to model the height of a person on a ferris wheel that is 100m tall and has a ride time of 25 minutes. Assume that you get on the ferris wheel on the ground and that the ground is at 0
h(t)=-50cos((2pix)/25)+50
convert
log_5(3x+5)=2
to exponential form
5^2=3x+5
What is the transformed y-value if the original y-value is 4 and the function has been vertically stretched by a factor of 3 and translated down 5?
4(3)-5=7
What are the quotient and remainder when
3x^4+2x^3-x^2+2x+15
is divided by (x-3)
3x^3+11x^2+32x+98
R=309
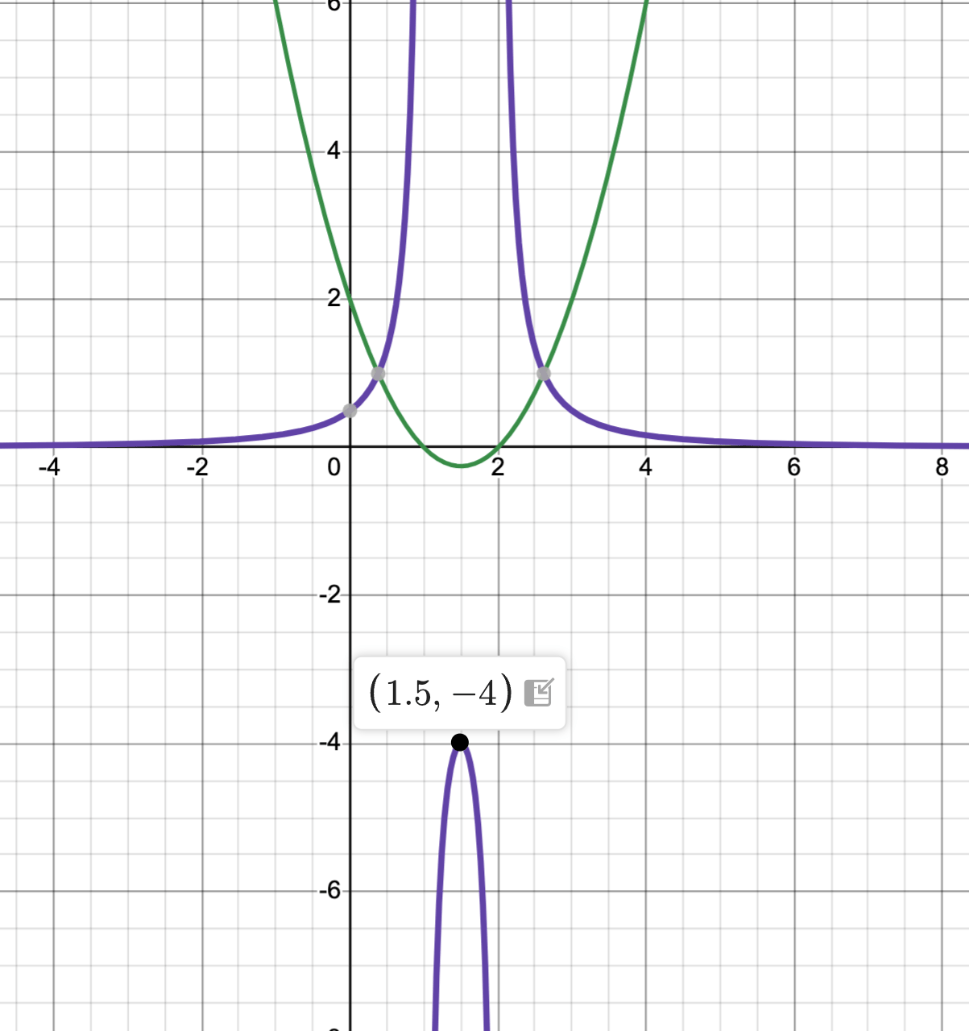
Sketch the reciprocal of the following function. Label the vertical asymptotes, horizontal asymptotes and local max. 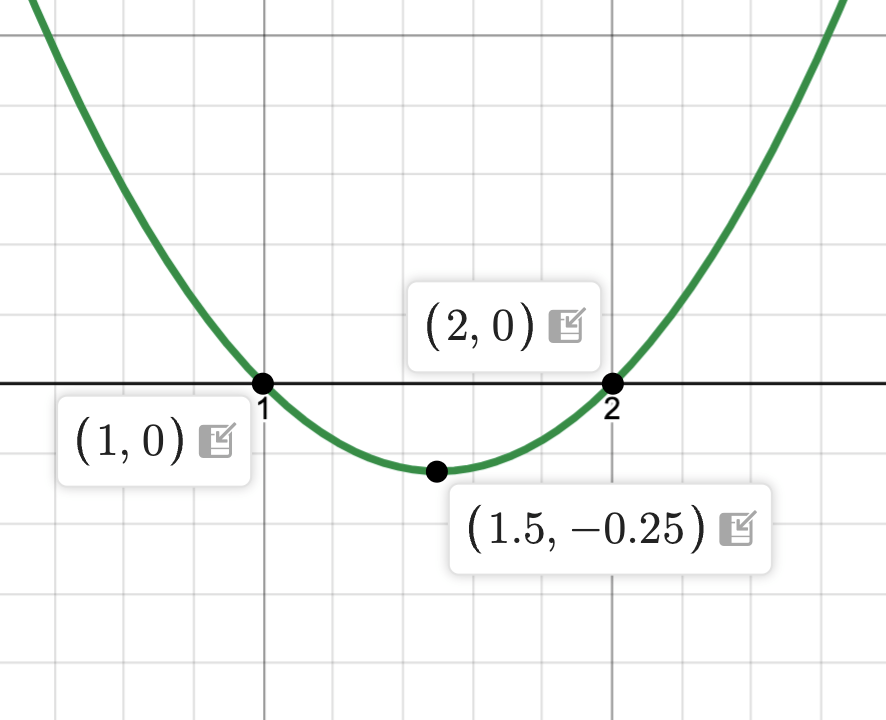
Convert from degrees to radians:
18^o
(18pi)/180 OR pi/10
using log laws, simplify the following logarithm
log(3x)-log(3y^2)+log(3x)
log((3x^2)/y^2)
Determine the symmetry of the following equation.
f(x)=-x(x^2-3)
ODD!
f(-x)=x(x^2-3)
What is the leading coefficient of the function that has x-intercepts at x=1, x=-3, and a double repeated root at x=5 and passes through the point (2,135)
3
determine the x-intercept, y-intercept, Vertical Asymptote, and horizontal asymptotes for the function
f(x)=(3x+2)/(5x-9)
x-intercept -2/3
y-intercept -2/9
V.A x=9/5
H.A y=3/5
solve the equation:
sin(x)=sqrt3/2
x=pi/3
x=2pi/3
solve the following equation
log_4(3x+1)+log_4(2x-3)=2
x=2.456
Determine the average rate of change between x=-2 and x=+4 for the function
f(x)=1/(x-5)
AROC=-0.143
solve the following equation for x
6x^3+19x^2+11x-11=-5
x=-1
x=-3/2 OR -1.5
x=1/3 OR 0.3333333333
solve for x. state the equation of vertical asymptotes, horizontal asymptotes, oblique asymptotes, and the location of any holes.
(x^{3}-5x^{2}-2x+24)/((x+3)(x-3))=0
V.A at x=-3
O.A y=x-5
Hole at x=3
Solutions, x=-2 x=4
if tan(x)=3/4 and sin(x) is negative, find
sin(x), cos(x), csc(x), sec(x), cot(x)
sin(x)=-3/5
cos(x)=-4/5
csc(x)=-5/3
sec(x)=-5/4
cot(x)=4/3
how many years has it been if an investment of $200 has grown to $500 at an interest rate of 3% compounded quarterly?
About 30.6 years have gone past
500=200(1+(0.03/4))^(4t)
The point (2,3) is on a function f(x). How would the point be changed for the new function
g(x)=-2f(3(x-4))+2?
x-> 2(1/3)+4=14/3
y-> 3(-2)+2=-4
(14/3,-4)
solve the inequality
15x^{3}-47x^{2}-2x+24>=0
[-2/3,4/5]U[3,infty]
for a bonus 100 points, find the error here
find the intervals that make the following true
-((2x+1)(x+2))/((3x+2)(7x+3)) <=0
(-infty,-2]U(-2/3,-1/2]U(-3/7,infty)
the equation that models the motion of a metronome arm is
f(x)=10sin((2pix)/0.5)
determine when during the first cycle, the metronome arm is 5cm to the left (assume negative is left) (if you get a negative answer, it is the quadrant 4 angle)
x_1=0.29167
x_2=0.45833
A substance takes 2hrs to decay from 27g to 10g. what is the substance's half life?
about 1.4 hours
What is the Instantaneous rate of change for the function at x=-3
f(x)=1/(x^2+5x)
IROC=0.0277