Interest Compounded Continuously Formula
A=Pert
Exponential Function
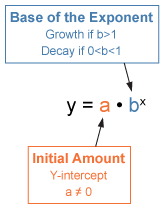
A function whose value is a constant (bb) raised to a power (xx).
Interest Compounded Formula
A=P(1+nr)nt
Exponential Decay
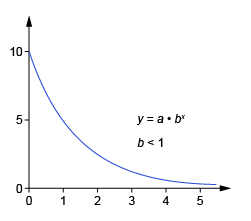
a relationship in which the change in y decreases at a rate proportional to its current value
Example.
y=a(1-r)^xy=a(1−r)x
Vertical Asymptotes
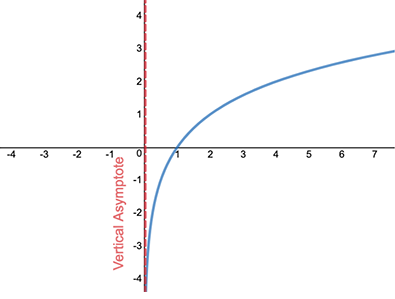
vertical lines that a graph approaches but does not intersect; found by setting the denominator of a rational function equal to 0 and solving for x
Product Property of Logarithms
logbxy=logb(x×y)=logbx+logby
Example.
log_{2}4x=log_{2} \left( 4 \times x \right) =log_{2}4_{}+log_{2}x_{}log24x=log2(4×x)=log24+log2x
Quotient Property of Logarithms
logbyx=logbx−logby
Example.
log_{5}\frac{24}{p}=log_{b}24-log_{b}plog5p24=logb24−logbp
Change of Base Property of Logarithms
logm(x)=logb(m)logb(x)
Example.
log_6(17)=\frac{log(17)}{log(6)}log6(17)=log(6)log(17)
Equality Property of Logarithms
If log_{b}x=log_{b}ylogbx=logby, then x=yx=y.
Example.
log_{3} \left( 2x-1 \right) =log_{3} \left( 3x+4 \right)log3(2x−1)=log3(3x+4), then \left( 2x-1 \right) = \left( 3x+4 \right)(2x−1)=(3x+4)
Exponential Growth
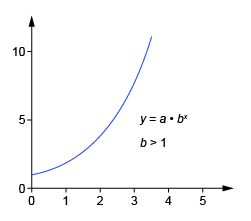
a relationship in which the change in y increases at a rate proportional to its current value
Example.
y=a(1+r)^xy=a(1+r)x
Horizontal Asymptotes
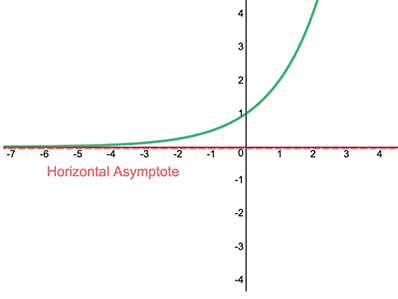
horizontal lines that the graph approaches but never intersects; found by comparing the degrees of the polynomials in the numerator and denominator in a rational function
Logarithm
The inverse function of the exponential function: the logarithm of a given number x is the exponent to which the given base, b, must be raised to produce that number, x
Example.
\log_{\text{base}}(\text{answer})=\text{exponent}logbase(answer)=exponent
Richter Scale
the logarithmic scale used for indicating the magnitude of an earthquake; the scale spans from one to ten, with ten being the strongest.
Power Property of Logarithms
logbxp=p×logbx
Example.
log_{4}x^{2}=2 \times log_{4}xlog4x2=2×log4x
Decibel
The unit for the loudness of sound and is abbreviated dB.
Joaquin deposits $1500 into a new savings account with an annual interest rate of 2.8%, compounded monthly. If he makes no deposits or withdrawals from the account, which of the following is the closest to the balance in the account after four years?
$1677.55
Which of the following functions models an exponential decay?
f(x)=2(0.5)ˣ
The current balance on an account with an initial principal of $10,000 is $20,000. The principal was invested at 6% annually, compounded continuously. Which of the following is closest to the amount of time the original $10,000 has been invested?
11.5 years
The population of a turtle species grows according to the logistic growth model, P \left( t \right) =\frac{4570}{1+34e^{-0.03t}}P(t)=1+34e−0.03t4570. How does the population change as the species grows?
The population increases then levels out at a carrying capacity.
If $12,000 is invested at an annual rate of 4.8% compounded continuously, about how long will it take the initial investment to double?
14 years
Ty invested $1500 in an account at a 3% interest rate compounded monthly. He also invested $1000 in a different account at a 5% interest rate compounded continuously. In how many years will the $1000 account be worth more than the $1500 account?
21
In September of 2010, the Sunday circulation of the Dallas Morning News fell to 373,815. This was a 4.3 percent decrease from the same period a year ago. If this rate continues, the Sunday circulation of the Dallas Morning News is likely to fall below 314,000 in four years. This change in circulation is an example of which of the following?
exponential decay
A conversation measures about 60 dB while a rock concert measures about 120 dB. How many times louder is the rock concert than the conversation?
1,000,000
A doctor prescribes a pain medication to a patient. Each hour, the effectiveness of the medicine decreases by 23%. The patient is given an initial does of 250 cc's of the medication. When the amount of medication in the patient's system reaches 50 cc's, a second dose can be given. How many hours after taking the initial dose can the patient take additional medicine?
6 hours
Newton's Law of Cooling uses the formula, kt=\ln\frac{T-S}{T_{0}-S}kt=lnT0−ST−S, where SS is the temperature of the room, TT is object temperature, and t is time. The temperature of a room is 70\degree F70°F. A cup of coffee is first poured at a temperature of 200\degree F200°F. After 10 minutes, the coffee temperature is 160\degree F160°F. How many minutes will it take for the coffee to reach a temperature of 140\degree F140°F?
16.73