Solving Advanced Functions
Solving Advanced Functions
Solving Advanced Functions
Solving Advanced Functions
Solving Advanced Functions
100
Radical Sign
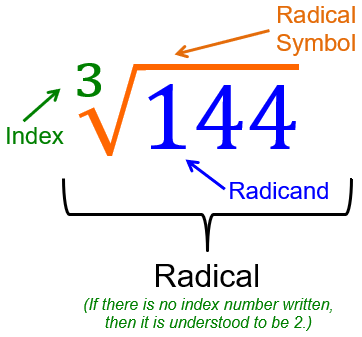
symbol used to indicate a root
Example.
\sqrt{121} = 11 121=11
100
Perfect Square
number whose square root yields a whole number
Example.
\sqrt{36}=636=6
100
Like Terms
terms with the same variable and exponent combination
Example.
2x2x and 5x5x
100
Factored
Separated into factors or divisors that, when multiplied together, yield the original number.
Example.
30 + 40 = (10\cdot3) + (10\cdot4)30+40=(10⋅3)+(10⋅4)
-2x-18 = -2(x+9)−2x−18=−2(x+9)
100
Irrational Numbers
real numbers that CANNOT be represented exactly; they can not be shown as a ratio of two integers nor placed on a number line
Example.
pi (π)
200
Order of Operations
PEMDAS: the set order in which multi-step equations must be solved: Parenthesis, Exponents, Multiplication and Division (left to right), Addition and Subtraction (left to right)
200
Square Root
the number, that when multiplied by itself, gives the square of the number
Example.
\sqrt{30} \times \sqrt{30} = 3030×30=30
200
Expression
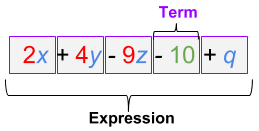
Numbers, symbols, and operators grouped together to show the value of something. Note that it differs from an equation because there is no equal sign and therefore cannot be solved, only simplified.
Example.
3x - 4y + 63x−4y+6
200
Combine Like Terms
method of simplifying an algebraic expression by adding or subtracting the coefficients of like terms
Example.
2x + 4x = 6x2x+4x=6x
200
Double Distribution
distributing terms through two sets of parentheses
known as FOIL when used on two sets of binomials in parentheses
Example.
(-3a+4b)(2a-5b)(−3a+4b)(2a−5b)
-3a(2a-5b)+4b(2a-5b)−3a(2a−5b)+4b(2a−5b)
-3a(2a)-3a(-5b)+4b(2a)+4b(-5b)−3a(2a)−3a(−5b)+4b(2a)+4b(−5b)
-6a^2+15ab+8ab-20b^2−6a2+15ab+8ab−20b2
-6a^2+23ab-20b^2−6a2+23ab−20b2
300
Dissecting (Math)
writing numbers or expressions in expanded form
Example.
10 = 5 + 510=5+5
6x = 2x + 4x6x=2x+4x
-24 = -4\cdot6−24=−4⋅6
4x = 4\cdot x4x=4⋅x
300
Distribution (mathematics)
Use of the distributive property where a number in front of a group of terms will multiply all terms in the grouping individually.
300
Distributive Property
a number in front of a group of terms will multiply all terms in the grouping individually
Example.
a(b+c) = ab + aca(b+c)=ab+ac
300
The graph of f(x)=x^{2}+3f(x)=x2+3 has two roots that can be seen in a viewing window of -10\leq x\leq 10−10≤x≤10, -10\leq y\leq 10−10≤y≤10. The graph of g(x)=200x^{2}-3g(x)=200x2−3 also has two roots that are not seen when graphed using the same window.
What would make it easier to read the value of the roots of g(x)g(x)?
The window needs to be zoomed in to discern the xx-values.
Explanation:
The graph of g(x)g(x) has a vertical stretch which will make the parabola skinnier than f(x)f(x). The graph will need to be zoomed in for the xx-values to find the roots.
300
Which of the following is equivalent to 8(8+y+y) -16y8(8+y+y)−16y for all values of y?
64
Explanation:
First, combine like terms inside the parentheses:
8(8+y+y) -16y\rightarrow8(8+2y) - 16y8(8+y+y)−16y→8(8+2y)−16y
Then, distribute the 8 to all terms inside the parenthesis:
8(8+2y)-16y\rightarrow(64 + 16y) - 16y8(8+2y)−16y→(64+16y)−16y
Remove the parentheses, then combine like terms:
(64 + 16y) - 16y \rightarrow 64+16y-16y\rightarrow64(64+16y)−16y→64+16y−16y→64
400
Asher makes $240 every pay period plus 15% on all sales. He determines his paycheck using the expression 240 + .15x240+.15x.
Which of the following is equivalent to Asher's expression?
5(48+.03x)
Explanation:
This expression factored (essentially "pulled out") the 5 from both terms. The distributive property proves this true:
5 × 48 = 2405×48=240
and
5 \times .03x = .15x5×.03x=.15x
400
A teacher is checking a student's work and notices their conclusion that 3(x-2)-(4x+5)=-1x-13(x−2)−(4x+5)=−1x−1.
Looking at their work, where is the first step with a mistake?
Step 1
3(x-2)-(4x+5)=3x-6-(4x+5)3(x−2)−(4x+5)=3x−6−(4x+5)
Step 2
3x-6-(4x+5)=3x-6-4x+53x−6−(4x+5)=3x−6−4x+5
Step 3
3x-6-4x+5=3x-4x-6+53x−6−4x+5=3x−4x−6+5
Step 4
3x-4x-6+5= -1x -13x−4x−6+5=−1x−1
Step 2
Explanation:
In step 2, the student forgot to distribute the negative in -(4x+5)−(4x+5) to both terms. This should become -4x - 5−4x−5.
400
The expression 3^{-3} \times 3^{2}3−3×32 is equivalent to:
31
Explanation:
This expression requires that the exponents be added together, resulting in 3^{-1}=\frac{1}{3}3−1=31.
400
Which of the following represents the cube root of a number to the fourth power?
(n4)1/3
Explanation:
The variable n was raised to the 4th power. It was then raised to the ⅓ power which is equivalent to taking the cubed root of the term.
400
Which of the following expressions is equivalent to 9x + 249x+24 for all values of x?
28+51(45x–20)
Explanation:
To distribute the \frac{1}{5}51 to each term inside the parentheses, divide each term by 5: 28 + \frac{1}{5}(45x – 20) =28 + 9x - 428+51(45x–20)=28+9x−4
Combine like terms: 9x + 249x+24
500
In order to add two fractions, a common denominator is used. Which of the following would be the appropriate step in adding the rational expressions \frac{5x-1}{x^{2}-3x+2}x2−3x+25x−1 and \frac{3}{2x-4}2x−43?
(22)x2−3x+25x−1+2x−43(x−1x−1)
Explanation:
To find a common denominator, first factor the denominators, then find the least common denominator.
\frac{5x-1}{x^{2}-3x+2}+\frac{3}{2x-4}=\frac{5x-1}{(x-2)(x-1)}+\frac{3}{2(x-2)}x2−3x+25x−1+2x−43=(x−2)(x−1)5x−1+2(x−2)3
The least common denominator is 2(x -1)(x - 2)2(x−1)(x−2). Therefore, multiply \frac{5x-1}{x^{2}-3x+2}x2−3x+25x−1 by (\frac{2}{2})(22) and multiply \frac{3}{2x-4}2x−43 by (\frac{x-1}{x-1})(x−1x−1).
500
Which expression is equivalent to \frac{3x+2}{x-1}-\frac{x+4}{3x+2}x−13x+2−3x+2x+4?
(x−1)(3x+2)8x2+9x+8
Explanation:
In order to find the difference between two rational expressions, first, find a common denominator, then combine the two fractions.
\frac{3x+2}{x-1}-\frac{x+4}{3x+2}x−13x+2−3x+2x+4
=\frac{ \left( 3x+2 \right) \left( 3x+2 \right) }{ \left( x-1 \right) \left( 3x+2 \right) }-\frac{ \left( x+4 \right) \left( x-1 \right) }{ \left( 3x+2 \right) \left( x-1 \right) }=(x−1)(3x+2)(3x+2)(3x+2)−(3x+2)(x−1)(x+4)(x−1)
=\frac{8x^{2}+9x+8}{ \left( x-1 \right) \left( 3x+2 \right) }=(x−1)(3x+2)8x2+9x+8
500
Three of the following expressions, when simplified, equal the same value. Which of the following equations, when simplified, is not equal to the other expressions?
(4x⋅3x)+y
Explanation:
Simplify the expression by multiplying the x-terms: (4x\cdot3x)+y= 12x^2 + y(4x⋅3x)+y=12x2+y This expression is not equivalent to the other three expressions.