A triangle is formed by connecting the origin to the point (2, -3)(2,−3) and then the point to the x-axis. Find \sin\thetasinθ.
13−3
Explanation:
The point is in Quadrant IV as is the triangle drawn, so the opposite of \thetaθ is -3−3 and the adjacent is 22. Use the Pythagorean theorem to find the hypotenuse, h=\sqrt{(-3)^2+2^2}=\sqrt{13}h=(−3)2+22=13 . The ratio for sine is opposite/hypotenuse so the ratio for this triangle is \sin\theta=\frac{-3}{\sqrt{13}}sinθ=13−3. Recall that sine is negative in the 4th quadrant.
Amplitude (of a Trigonometric Function)
The height from the mean, or rest, value of the function to its maximum or minimum.
Period (of a Trigonometric Function)
One cycle of a trigonometric function.
Phase Shift (of a Trigonometric Function)
When there is a value added or subtracted to the function or within the function.
Law of Sines
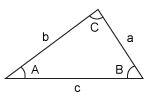
an equation that relates the lengths of the sides of a triangle to the sines of the triangle's angles
\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}sinAa=sinBb=sinCc
Law of Cosines
equations that relate the lengths of the sides of a triangle to the cosines of the triangle's angles
c^{2}=a^{2}+b^{2}-2ab \left( cosC \right)c2=a2+b2−2ab(cosC)
b^{2}=a^{2}+c^{2}-2ac \left( cosB \right)b2=a2+c2−2ac(cosB)
a^{2}=b^{2}+c^{2}-2bc \left( cosA \right)a2=b2+c2−2bc(cosA)
While reviewing for a unit test, students enter the command tan \left( \frac{ \pi }{2} \right)tan(2π) into their calculators and receive an error message. A discussion of which of the following topics would be most helpful for the students?
the domains of the trig functions
Explanation:
The problem is with the input value. A discussion or review of the domain for tangent functions would be important.
If -\frac{\pi }{2}\leq \sin^{-1}x\leq \frac{\pi }{2}−2π≤sin−1x≤2π, find the exact value of the expression: \tan\left (\sin^{-1}(\frac{-\sqrt{2}}{2}) \right )tan(sin−1(2−2) ).
−1
Explanation:
Using knowledge of the Unit Circle:
\tan\left (\sin^{-1}(\frac{-\sqrt{2}}{2}) \right )=\tan(-\frac{\pi }{4})=-1tan(sin−1(2−2) )=tan(−4π)=−1
Given cscx=4cscx=4, find a possible value of cosxcosx.
415
Explanation:
cscx=\frac{hypotenuse}{opposite}=\frac{4}{1}cscx=oppositehypotenuse=14. cosx=\frac{adjacent }{hypotenuse}cosx=hypotenuseadjacent. The hypotenuse was given as 4, using the Pythagorean theorem can be used to find the adjacent side. 4^{2}-1^{2}=x^{2} \rightarrow 15=x^{2} \rightarrow x=\sqrt{15}42−12=x2→15=x2→x=15. So it is possible for cosx=\frac{\sqrt{15}}{4}cosx=415.
What is the period of the function y=\frac{1}{4}cos \left( \frac{1}{2}x- \pi \right)y=41cos(21x−π)?
4π
Explanation:
Given the form y=ay=a cos \left( bx-c \right) +dcos(bx−c)+d, the period of a cosine function will be period = \frac{2 \pi }{b}b2π. For this function, b = ½ so the period is \frac{2 \pi }{1/2}=4 \pi1/22π=4π.
Over the interval 0 \leq x \leq 2 \pi0≤x≤2π, solve sin(4x) = \frac{-1}{2}sin(4x)=2−1.
7π,2411π
Explanation:
First, use the unit circle to evaluate where sin(x) = \frac{-1}{2}sin(x)=2−1. This is true in the third and fourth quadrants and produces \frac{7\pi}{6} ,\frac{11\pi}{6}67π,611π. Next, set each value of x equal to 4x4x so that:
4x = \frac{7\pi}{6} \rightarrow x = \frac{7\pi}{24}4x=67π→x=247π and
4x = \frac{11\pi}{6} \rightarrow x = \frac{11\pi}{24}4x=611π→x=2411π
Simplify the expression: \frac{1+\cos 2x}{1-\cos 2x}1−cos2x1+cos2x
cot2(x)
Explanation:
\frac{1+\cos 2x}{1-\cos 2x}\rightarrow \frac{1+2\cos^2x-1}{1-1+2\sin^2x}\rightarrow \frac{2\cos^2x}{2\sin^2x}\rightarrow \frac{\cos^2x}{\sin^2x}\rightarrow \cot^2x1−cos2x1+cos2x→1−1+2sin2x1+2cos2x−1→2sin2x2cos2x→sin2xcos2x→cot2x
A group of students has concluded that tan \left( \frac{x}{2} \right) =\frac{1}{2}=tan(x)tan(2x)=21=tan(x). Which of the following is the best way to lead them to discover the correct way to derive the trig identity for tan \left( \frac{x}{2} \right)tan(2x)?
Derive a different, correct trig identity, on the board.
Explanation:
A guided, modeled discovery, using trig identities that have already been studied, will show students how to use a table of trig identities to derive the new identity and the logic to follow when deriving the identity.
The circle below has a triangle inscribed inside of it. What is the magnitude of the area of the circle?
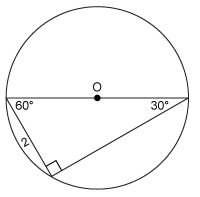
4π
Explanation:
Since this is a 30-60-9030−60−90 triangle, rules of special triangles can be used. The side across from the 30\degree30° is 22, so the hypotenuse is 44. The hypotenuse of the triangle is also the diameter of the circle so the radius of the circle is 22. The area is then A=\pi r^{2}=\pi (2)^{2}=4\piA=πr2=π(2)2=4π.