Limits
Derivatives
Assorted Precalculus
Grab Bag
100
Evaluate the limit.
\lim_{x\rightarrow 0}1/x
The limit does not exist!
100
Find the derivative of the function.
f(x)=\sqrt{x}-1/\sqrt{x}
f'(x)=\frac{1}{2\sqrt{x}}+\frac{1}{2x^{3/2}}
100
The exact value of
\cos({5pi}/6)
-\sqrt{3}/{2}
100
The average rate of change of
f(x)=-3x^2
over the interval [1, 3].
-12
200
Evaluate the limit.
\lim_{x\rightarrow 0}\frac{1-e^{-2x}}{\secx}
0
200
Find the derivative of the function.
f(x)=\frac{x^3-5}{\ln x}
f'(x)=\frac{3x^2\ln x-x^2+5/x}{(\ln x)^2}
200
The exact value of
tan(\frac{3\pi}{4})
-1
200
The population of a bacterial colony is approximately
P(t)=100+61t+3t^2
thousand, t hours after observation begins. Find the rate the colony is growing after 5 hours.
91 thousand bacteria per hour
300
Evaluate the limit.
\lim_{h\rightarrow 0}\frac{\sin(x+h)-\sin(x)}{h}
\cos x
300
Find the derivative of the function.
f(x)=\cos(\tan(7x))
f'(x)=-7\sin(\tan(7x))\sec^2(7x)
300
\text{The value of } \sec\theta \text{ when}
\sin\theta=-\frac{2}{3} \text{ and } \pi<\theta<\frac{3\pi}{2}
-\frac{3\sqrt{5}}{5}
300
400
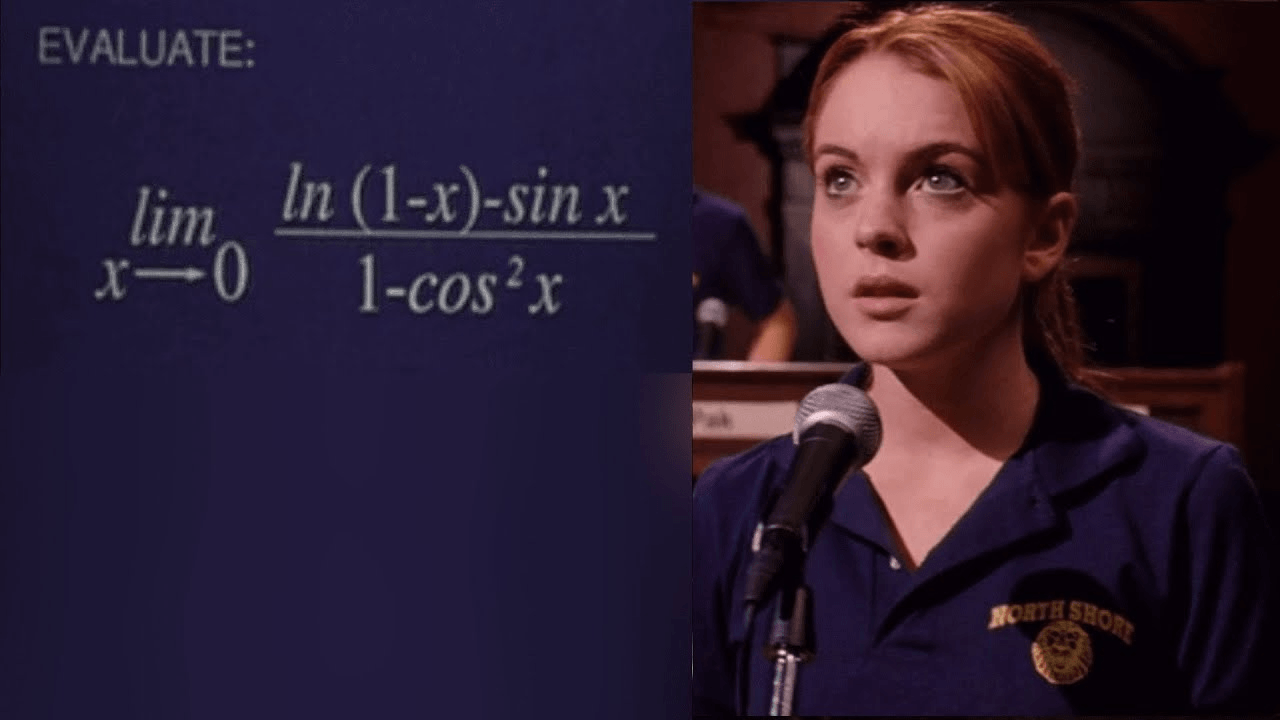
Evaluate the limit.
\lim_{x\rightarrow 0}\frac{\cos x-1}{x^2}
-1/2
400
Find the derivative of the function.
f(x)=\tan^{-1}(4x^3)-\ln(x^2+4)
f'(x)=\frac{12x^2}{1+16x^6}-\frac{2x}{x^2+4}
400
The exact solution to the equation
e^{2x}-4e^x-10=2
x=\ln6
400
Find an equation for the tangent line to the graph of
\sqrt{x}+\sqrt{y}=3
at the point (4,1).
y-1=-1/2(x-4)
500
Evaluate this limit.
\lim_{x\rightarrow 0}\frac{\tan x-x}{x^3}
1/3
500
Find the derivative, dy/dx .
x^2y^3=\csc(5x)+2x
dy/dx=\frac{2-5\csc(5x)\cot(5x)-2xy^3}{3x^2y^2}
500
The exact solution to the equation below.
\ln(x)+\ln(x-3)=\ln(7x)
x=10
500
Find the critical points of the function
f(x)=\frac{x^2+3}{x+1}
{-3,-1,1}