Chapter 6:
Exponential Functions
Exponential Functions
Chapter 6:
Logarithmic Functions
Logarithmic Functions
Chapter 7:
Rational Functions
Rational Functions
Chapter 10:
Trigonometric Functions
Trigonometric Functions
Chapter 11:
Sequences and Series
Sequences and Series
100
Rewrite in logarithmic form:
14^3 = 2744
log_14 2744 = 3
100
Rewrite in exponential form:
log_12x = 8
12^8 = x
100
Graph and write the asymptote equations:
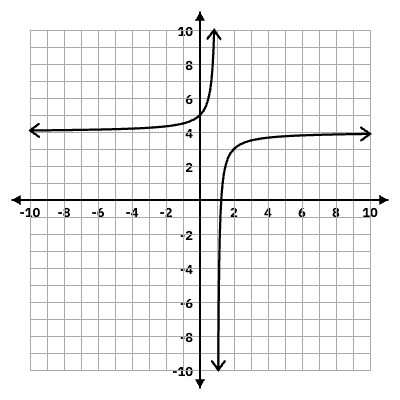
y = -1/(x - 1) + 4
x = 1, y = 4
100
Solve for x. Round to the nearest tenth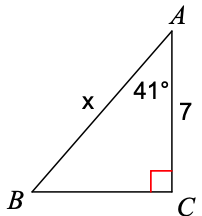
9.3
100
Evaluate the infinite sum of the series:
2 - 1 + 1/2 - 1/4 + ...
4/3
200
Sketch a graph of the following function and write the asymptote equation.
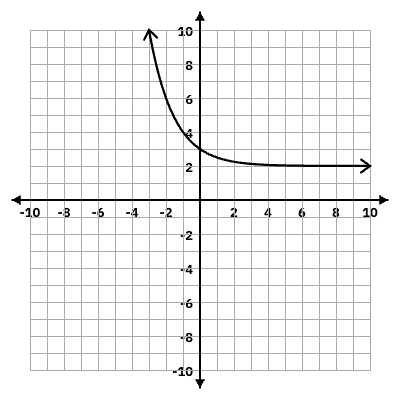
y = (1/2)^x + 2
y = 2
200
Evaluate:
log_4 64
3
200
Graph and list the asymptote equations:
y = (3x - 2)/(x + 3)
y = 3, x = -3
200
Evaluate:
cos(-(11pi)/6)
sqrt(3)/2
200
Find the 38th term of the arithmetic sequence whose common difference is -10 and whose second term is -39
-399
300
Sketch a graph of following function and write the asymptote equation.
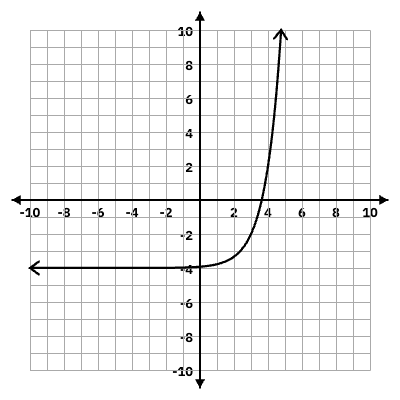
y = 3(2)^(x - 3) - 4
y = -4
300
Expand:
log((3x^2)/8)
log3 + 2logx - log8
300
Simplify:
(x^2 + 4x - 12)/(x^2 - 10x + 16) -: (x + 6)/(6x - 48)
6
300
The terminal side of an angle goes through the point (-4, -3). Evaluate the cosecant and secant of that angle.
csc(theta) = -5/3
sec(theta) = -5/4
300
Write the rule for the geometric sequence given
a_3 = 36, a_6 = 7776
a_n = 6^(n-1)
400
Solve:
17^(10x) - 4 = 52
x = (log_17(56))/10
x = (log56)/(10log17)
400
Graph the function and write the asymptote equation:
f(x) = log_3(x + 6) + 2
x = -6
400
Simplify. You final answer should be fully factored.
(3x)/(x + 6) - 4/(x + 1)
((3x + 8)(x -3))/((x+ 6)(x+1))
400
Graph and define the period:
y = -2cos(x/2) + 4
Period =
4pi
400
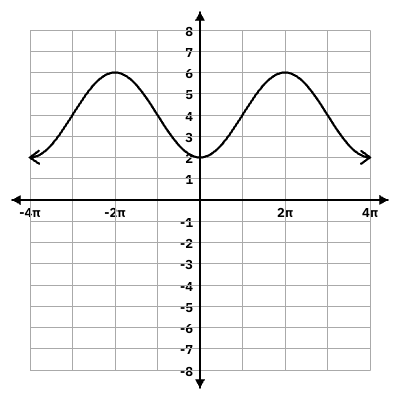
Evaluate the first 16 terms of the following series:
26 + 35 + 44 + 53 + ...
1496
500
Solve:
-8e^(x + 5) - 1 = -88
x = ln(87/8) - 5
500
Solve:
log_9x + log_9(x + 24) = 2
x = 3
500
Solve:
1/(x - 5) = (5x + 15)/(x + 2) - 1/(x^2 -3x - 10)
x = 26/5, -3
500
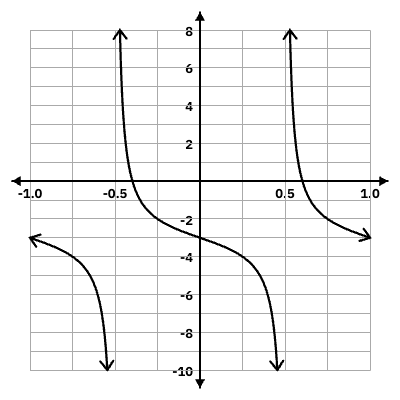
Graph and write the repeating asymptote equation:
y = -tan(pix) - 3
x = 1/2 + n
500
Evaluate:
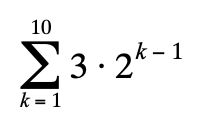
3069