Features of Functions
Adding Functions
Analyzing Functions
Interpreting Graphs
More Features of Functions
100
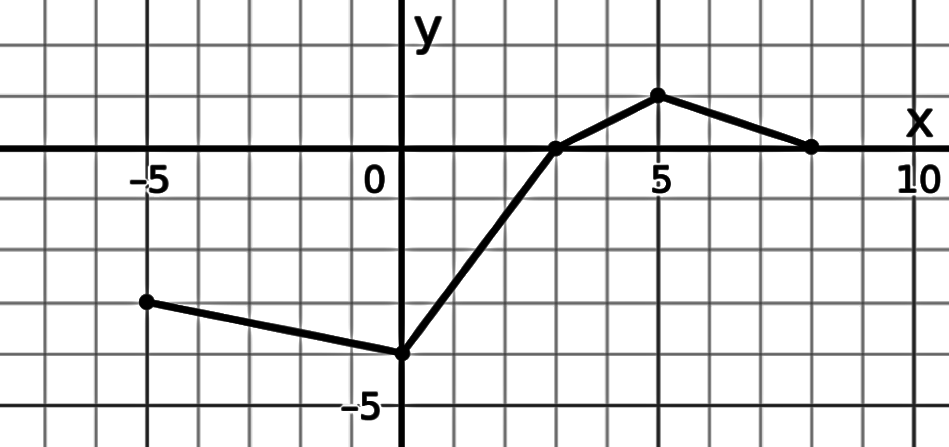
What are the coordinates of the y-intercept?
(0, -4)
100
a(x) = 4x + 6, b(x) = 2x + 3
c(x) = a(x) + b(x)
c(x) = ?
c(x) = 6x + 9
100
Given the function d(t) = 10t...
If t = 5, we have d(5). What does d(5) equal?
d(5) = 10(5)
d(5) = 50
100
If x = 3, f(3) =
0
100
What are the coordinates of an x-intercept?
(3, 0) and (8, 0)
200
What are the coordinates of the absolute minimum?
(0, -4)
200
d(x) = 5x + 8, e(x) = 3x - 4
f(x) = d(x) + e(x)
f(x) = ?
f(x) = 8x + 4
200
Given the function d(t) = 10t...
If d(t) = 80, what does t equal?
80 = 10t
t = 8
200
If f(x) = 1, then x =
5
200
What are the coordinates of the absolute maximum?
(5, 1)
300
What is the domain of the graph (the set of all the x-values, set inside [brackets])?
[-5, 8]
300
a(x) = 9x + 4, b(x) = -6x + 3
c(x) = a(x) + b(x)
c(x) = ?
c(x) = 3x + 7
300
The distance that a dog can run in feet is measured based on how many seconds he has been running. This distance can be modeled by the function d(t) = 10t, where d(t) is the distance in feet at time t in seconds.
How far has the dog run in 3 seconds?
30 feet
3 seconds means t = 3
300
If x = -5, f(-5) =
-3
300
What is the range of the graph (the set of all the y-values, set inside [brackets])?
[-5, 1]
400
What is the interval of increase? In [brackets].
[0, 5]
400
d(x) = -8x - 6, e(x) = 3x + 14
f(x) = d(x) + e(x)
f(x) = ?
f(x) = -5x + 8
400
The distance that a dog can run in feet is measured based on how many seconds he has been running. This distance can be modeled by the function d(t) = 10t, where d(t) is the distance in feet at time t in seconds.
If the dog has run 60 feet, how long has the dog been running?
6 seconds
60 feet means d(t) = 60
400
If f(x) = -4, x =
0
400
What is an intervals of decrease? In [brackets]
[-5, 0] U [5, 8]
500
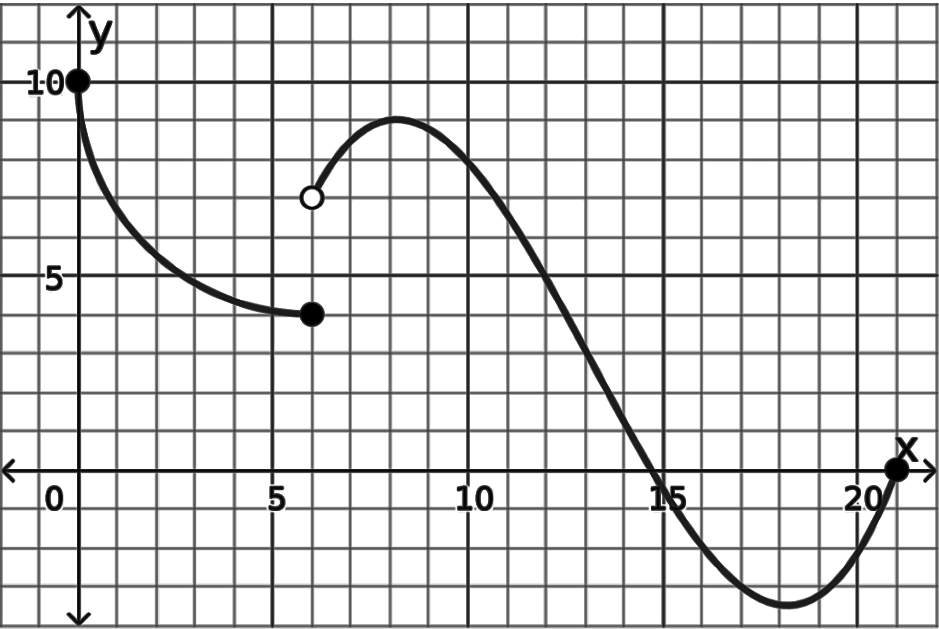
What is the domain of the graph (the set of all the x-values, set inside [brackets])?
[0, 21]
500
The Flash and Quicksilver are trying to see how many steps they take while running around in a blizzard. The function that models the number of steps the Flash takes each second is f(t) = 12t + 50. The function that models the number of steps Quicksilver takes is q(t) = 15t + 120. Find the function s(t) that represents the number of steps that both take put together; s(t) = f(t) + q(t).
s(t) = 27t + 170
500
The distance that a dog can run in feet is measured based on how many seconds he has been running. This distance can be modeled by the function d(t) = 10t, where d(t) is the distance in feet at time t in seconds.
How long has the dog been running if d(t) = 255?
25.5 seconds
d(t) = 255, 255 = 10t. Divide both sides by 10.
500
If x = 4, f(4) =
0.5 or 1/2
500
What is the range of the graph (the set of all the y-values, set inside [brackets])?
[-3.5, 10]