"Simplify" sqrt(12x^3)
2xsqrt(3x
Simplify by substracting:
(4x^4-3x^3-x+7)-(-3x^3+2x^2+x)
4x^4-6x^3-2x^2-2x+7
"Factor completely " 2x^3 - 4x^2 - 48x
2x(x + 4)(x - 6)
Simplify:
(x^2 + x - 12)/(x - 3)
x + 4
What high school did Coach Mawhorter graduate from?
Central Noble
"Simplify": (12x^3y^-2z^6)/(27x^5y^4
(4z^6)/(9x^2y^6)
Multiply the following:
(4x - 6)(2x + 1)
8x2-8x-6
Solve the equation by factoring it:
12x2 - 7x - 10 = 0
x = -2/3, 5/4
Simplify and multiply:
(x^2 - 5x + 6)/(5x^2) * (10x)/(x - 2)
(2(x - 3))/(x)
What High school did Mr. Baumgartner graduate from?
Fairfield
Write the equation of the line for the table of values below.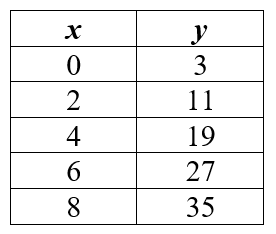
y = 4x + 3
Divide (3x2 - 5x + 1) by (x + 1)
3x-8 + 9/(x+1
Solve the quadratic equation by using the quadratic formula
x2 - 2x - 5 = 0
x=(-b +- sqrt(b^2-4qac))/(2a
x = 3.45, -1.45
Solve for x:
14/(2x) = 20/27
x = 9.4
What college did Mr. Grady graduate from?
Purdue
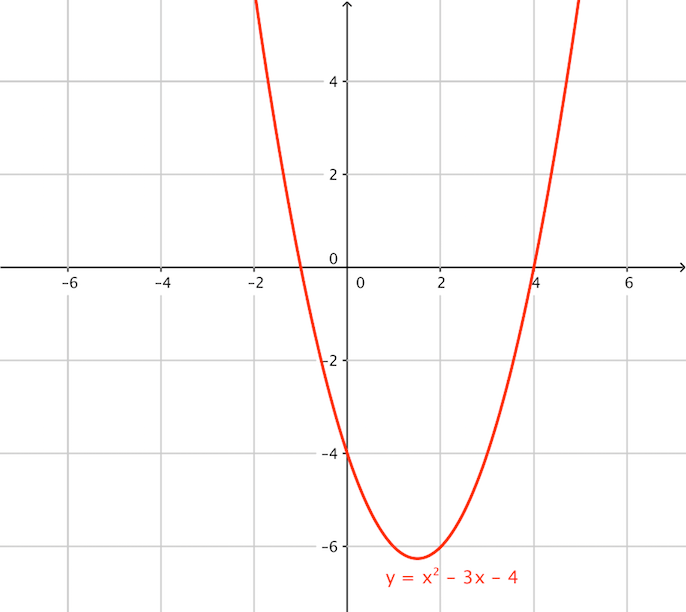
Graph the quadratic equation listed below:
y = x2 - 3x - 4
Factor completely:
6a2b - 12ab3 + 3ab
3ab(2a - 4b2 + 1)
A ball is thrown into the air with an initial velocity of 4 meters per second from a height of 2 meters. Find when the ball will be at its maximum height and when will the ball hit the ground?
P(t) = -4.9t^2 + v_0t+h_0, where v = velocity and h = height
P(t) = -4.9t2 + 4t + 2
(-b)/(2a) = (-4)/(2(-4.9) )=0.41
It is at its maximum after 0.41 seconds.
0 = -4.9t2 + 4t + 2
It will hit the ground at 1 second.
Solve for x:
(x - 3)/4 = (3x + 1)/7
x = -5
What high school did Mr. Tuggle graduate from?
East Noble
Determine whether the table of values below is a linear function, quadratic or exponential.

This is exponential. The equation is
y=2(3)^x
A square has an area of 42.25 inches squared. What is the length of one side of the square?
x2 = 42.25
x = sqrt(42.25
x = 6.5
A garden is 4 ft wide and 8 feet long. The length and the width will be increased by x feet. If the new area is to be 77 feet squared, then what is x and the new dimensions of the garden?
x = 3
Dimensions are 7 feet wide and 11 feet long.
Solve for x:
(x + 3)/(x - 2) = (x - 4)/(x + 5)
x = -1/2
What school did Mrs. Newby teach at before West Noble?
Howe