Evaluating Exp. Functions
Exponential Growth
Exponential Decay
Exponential vs. Linear
100
If f(x) = 10(2)^x then which of the following represents the value of f(0) ? (1) 1 (2) 0 (3) 10 (4) 20
(3) 10
100
Which of the following is the equation of an increasing exponential function? 1) y = 4(0.75)^x 2) y = 7(3/2)^x 3) y = 5x - 2 4) y = 3x^2
2) y = 7(3/2)^x
100
You buy a car for $10,000. It loses value at a rate of 34% per year. Write a model to represent the car's value over time.
What is y = 10,000(0.66)t?
100
Fill in the blanks: A linear function ____________ or ____________ by the same amount. An exponential function ____________ or ______________ by the same amount.
add/subtracts multiplies/divides
200
Given the function f(x)= (3)(0.5)^x Evaluate the function when x = -4
f(-4) = 48
200
You deposit $500 in a bank account with a 7% interest rate that is compounded yearly. How much money will you have in your account in 7 years, rounded to the nearest cent.
What is $802.89?
200
You buy a car for $10,000. It loses value at a rate of 34% per year. How much will your car be worth in 12 years? Round your answer to the nearest cent.
$68.32?
200
The table below shows the average yearly balance in a savings account where interest is compounded annually. No money is deposited or withdrawn after the initial amount is deposited.
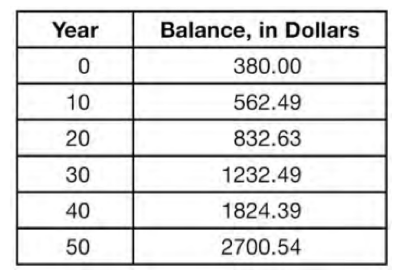
Which type of function best models the given data?
1) linear function with a negative rate of change 2) linear function with a positive rate of change 3) exponential decay function 4) exponential growth function
4) Exp. Growth Function
300
The value in dollars, v(x), of a certain car after x years is represented by the equation v(x) = 25,000(0.86)^x. To the nearest dollar, how much is the car worth after four years. 1) 2,589 2) 6,510 3) 13,675 4) 18,490
3) 13,675
300
The equation A = 1300(1.02)^7 is being used to calculate the amount of money in a savings account. What does 1.02 represent in this equation?
1. 0.02% decay 2. 0.02% growth 3. 2% decay 4. 2% growth
4. 2% growth
300
You buy a car for $15,000. It loses value at a rate of 17% per year. Write a model to represent the car's value over time.
What is y = 15000(0.83)t?
300
Determine whether T(x) is a linear or exponential function?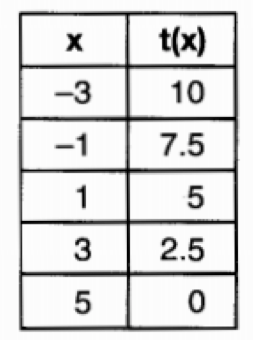
T(x) is defined as a linear function because the RATE OF CHANGE IS CONSTANT.
400
The value in dollars, v(x), of a certain car after x years is represented by the equation v(x) = 25,000(0.86)^x . To the nearest dollar, how much more is the car worth after 2 years than after 3 years? 1) 2,589 2) 6,510 3) 15,901 4) 18,490
1) 2,589
400
A population of 1,000 bacteria on the outside drinking fountain doubles in size every hour. Write an equations that models this situation.
What is y = 1000(2)t?
400
For a recently released movie, the function y = 119.67(0.61)^x models the revenue earned, y, in millions of dollars each week, x, for several weeks after its release. Based on the equation, how much more money, in millions of dollars, was earned in revenue for week 3 than for week 5? 1) 37.27 2) 27.16 3) 17.06 4) 10.11
3. 17.06
400
If you were to explain to a friend in Algebra class the major difference between a linear and exponential function, what would you say to them?
Linear functions have a CONSTANT RATE OF CHANGE, while exponential functions have a constant MULTIPLYING FACTOR.
500
A population of 1,000 bacteria on the outside drinking fountain doubles in size every hour. How many bacteria will there be in one fourth of a day.
64,000 bacteria.
500
Is this an exponential growth or decay function? What is the growth or decay factor? y = 112(2/3)t?
Decay and the decay factor is (2/3)