Are the following two lines parallel, perpendicular, or neither?
3y -2x = 9
6x = -4y -5
Perpendicular
Find the inverse of the relation: {(2, 3), (4, -6), (-1 1), (-1, -1)}
{(3, 2), (-6, 4), (1, -1), (-1, -1)}
Write the equation of a line with slope 3/4 and y-intercept 3 in all 3 forms.
y - 3 = 3/4 (x - 0)
y = 3/4 x + 3
3x - 4y = -12
Determine whether the graph shows positive, negative, or no correlation. Describe its meaning if positive or negative. 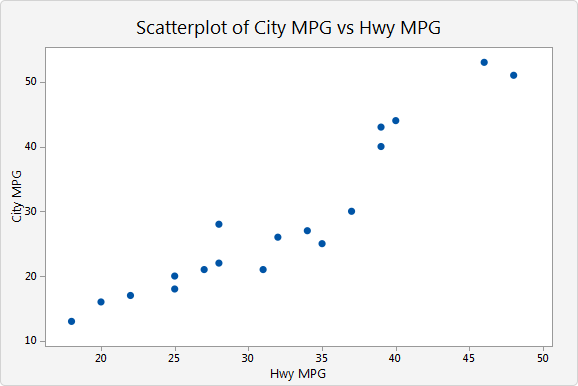
Positive Correlation
As the Highway MPG increases, so does the City MPG
Find the equation of the line in point slope, slope intercept, and standard form that is parallel to the line 4y = 3x - 35 and goes through the point (2,5)
y - 5 = 3/4 (x -2)
y = 3/4 x + 7/2
3x - 4y = -14
Find the inverse of f(x) = -5x + 4 and graph both the lines.
f-1(x) = -1/5 x + 4/5
Write an equation in all three forms that passes through the points (-2, 5) and ( 8, -1)
y - 5 = 3(x + 2)
y = 3x + 11
3x - y = -11
Determine whether the graph shows positive, negative, or no correlation. Describe its meaning if positive or negative.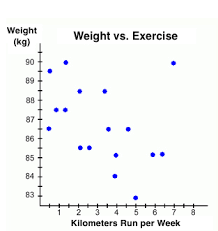
Negative Correlation
As you run more, your weight decreases.
Find the equation of the line in point slope, slope intercept, and standard form that is perpendicular to -3y + 5 = x that goes through the point (1,1).
y - 1= 3(x - 1)
y = 3x - 2
3x - y = 2
Find the inverse and graph both lines: 4x + 3y = 7
f-1(x) = -3/4 x + 7/4
Find the equation of the line in point slope, slope intercept, and standard form going through the x-intercept and perpendicular to -7x = 7y + 2.
y - 0 = 1 (x + 2/7)
y = x + 2/7
x - y = -2/7
The population of unicorns decreased at a constant rate of 12 unicorns per year. In the year 500 the population of unicorns was 5,000. Write an equation to represent the unicorn population in years after the year 400. Predict the population of unicorns in the year 600.
y = -12x + 6200
3,800 unicorns.
Are the following equations perpendicular, parallel, or neither?
-3x + 2y = 7
12x = 8y - 28
Neither, they are the same line.