Sequences
Exponents 7.1 & 7.2
Word Problems
Exponents 7.3 & 7.4
Graphing
100
Is the sequence arithmetic, geometric, or neither? Explain.
frac{1}{2}, 2, 3\frac{1}{2}, 5, 6\frac{1}{2}
The sequence is arithmetic because we add 1 1/2 each time.
100
Simplify:
(5u^4v)(7u^4v^3)
35u^8v^4
100
Paige invested $1200 at a rate of 5.75 % compounded quarterly. Determine the value of her investment after 7 years.
$1,789.54
100
Express the answer in both standard form and scientific notation.
(2 * 10^3)(2*10^3)
4*10^6; 4,000,000
100
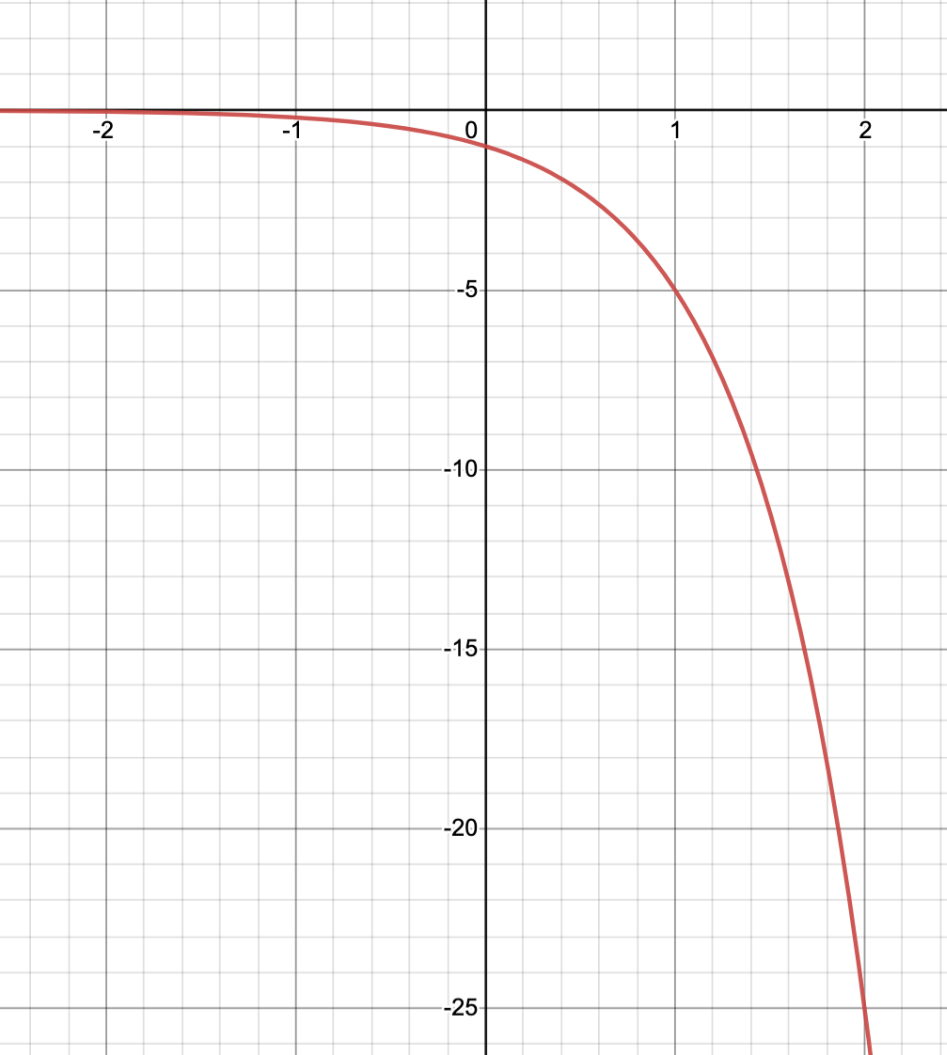
Graph and find the y-intercept, domain, and range:
y = -5^x
D: {all real numbers}
R: { y < 0}
y-int: (0, -1)
200
Determine if the sequence is arithmetic, geometric, or neither. Explain. Write a formula if possible.
2, -3, 4.5, -6.75, ...
The sequence is geometric because you multiply by -1.5 each time.
a_n = 2 * (-1.5)^{n-1}
200
Simplify:
(4x)^2 (x^3y)^3(y^5)
16x^{11}y^8
200
Camilo purchased a rare coin from a dealer for $300. The value increases at 5% each year. Write an equation to model the value over time. Use the equation to find the value after 5 years.
y =300*(1.05)^x, \$ 382.88
200
Express the answer in both standard form and scientific notation.
\frac{2 * 10^{-8}}{4 * 10^{-2}}
5 *10^{-7}; 0.0000005
200
Graph and find the y-intercept, domain, and range:
y = 6^x-3
D: {all real numbers}
R: { y > -3}
y-int (0, -2)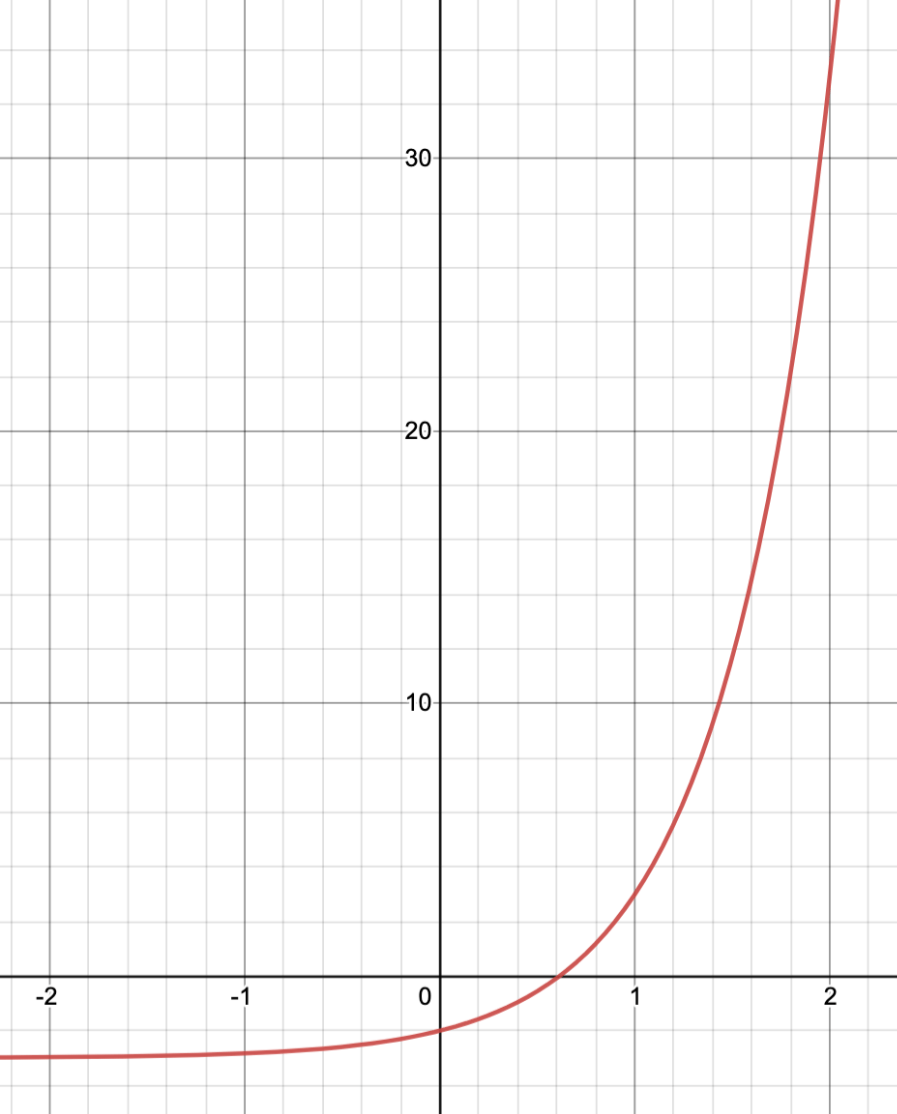
300
Write an equation to find the nth term and find the 10th term of the sequence: 6, -24, 96, ...
a_n = 6 *(-4)^{n-1}, -1,572,864
300
Simplify:
\frac{r^4t^7v^2}{t^6v^5}
\frac{r^4t}{v^3}
300
Leonardo purchases a car for $18,995. It depreciates at a rate of 18% per year. Create an equation to represent the car's value over time. After 6 years how much is it worth?
y = 18995*(0.82)^x, \$5,774.61
300
Simplify:
25^{3/2}
125
300
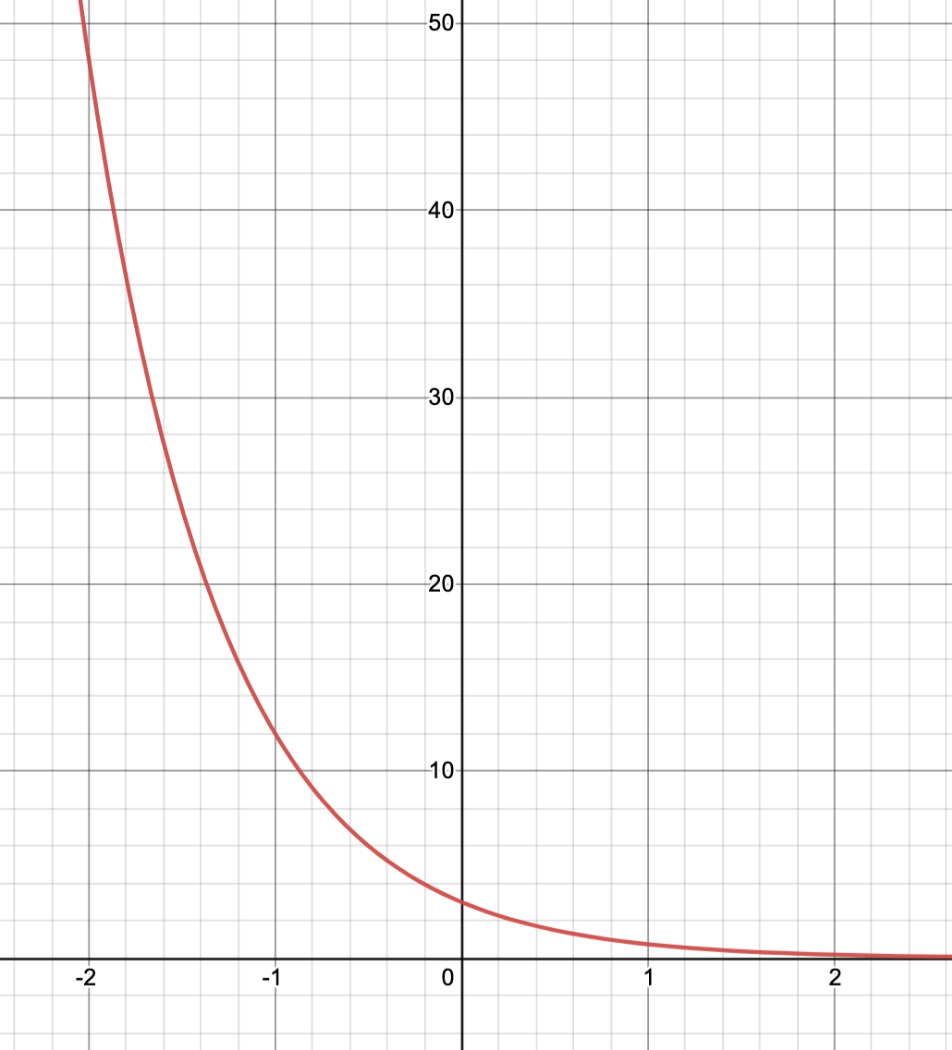
Graph and find the y-intercept, domain, and range:
y = 3(1/4)^x
D: { all real numbers}
R: {y >0}
y-int (0, 1)
400
Write an equation to find the nth term and find the 10th term of the sequence: 768, -576, 432, -324, ...
a_n = 768(-3/4)^{n-1}
a_10 =-57.665
400
Simplify:
\frac{2a^2b^{-7}c^10}{6a^{-3}b^2c^{-3}}
\frac{a^5c^13}{3b^9}
400
Jin's investment of $4,500 has been losing value at a rate of 2.5 % each year. Create an equation to represent the value of the investment over time and find the value after 5 years.
y = 4500 (1- 0.025)^x, \$3,964.93
400
Simplify:
9^{-\frac{3}{2}}
\frac{1}{27}
500
Danielle's parents have offered her two different options to earn her allowance for a 9 week period over the summer. She can either get paid $30 each week or $1 the first week, $2 the second week, $4 the third week, and so on. Find the total she would get paid with each option. Which should she choose?
$270 with the first and $511 with the second. She should choose the second one because she will earn $241 more.
500
Simplify:
\frac{(x^2y^{-4}z^5)^0}{(2x^-5y^7z^5)^{-2}}
\frac{4y^{14}z^{10}}{x^{10}}
500
Solve for x:
5^x = \frac{1}{25}
x = -2
600
Simplify:
(\frac{-3x^{-6}y^{-1}z^{-2}}{6x^{-2}yz^{-5}})^{-2}
\frac{4x^8y^4}{z^6}
600
Solve for x:
4^x = 32
x = \frac{5}{2}