Characteristics of Quadratics
Graphing Quadratics
Quadratics in REAL LIFE
MORE Quadratics in REAL LIFE
100
7)
a) What is the vertex? ______________
(3, 1)
100
9. Use the quadratic function y=3x2+12x+8 to find the following.
d) The y-intercept
(0, 8)
100
2. Suppose a ball is thrown upward with an initial upward velocity of 30 meters per second from an initial height of 10 meters. Write an equation for the height over time.
h = -4.9t2 + 30t + 10
100
a) How long was the firework in the air?
14 seconds
200
7.
b) Where is the axis of symmetry? (Sketch and label it.)
x = 3
200
9. Use the quadratic function y=3x2+12x+8 to find the following.
a) The equation for its axis of symmetry
x = -2
200
3. The following graph models the path of an object, in feet, being projected into the air. Answer the following questions using the model.
a) How high did the object go?
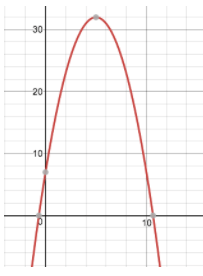
32 feet
200
b) How high did it go?
784 feet
300
8. Does graph of the equation y= -(x+5)(x+7) have a maximum or a minimum value? Explain how you know.
This graph would have a MAXIMUM because the a value is negative. Therefore, it would open down and the y-value of the vertex would be negative.
300
9. Use the quadratic function y=3x2+12x+8 to find the following.
b) The vertex
(-2, -4)
300
3. The following graph models the path of an object, in feet, being projected into the air. Answer the following questions using the model.
b) How long was the object in the air?
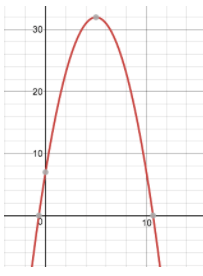
10.5 seconds
(approximately)
300
c) How high was the firework when it was first lit? How do you know?
15 feet
(I know this because this is the height at the starting time of 0 seconds - initial height)
400
10. Determine the vertex for the following quadratic y-3=(x-4)2
(4, 3)
400
(100 points for each part)
y-intercept: (0, 3)
Axis of symmetry: x = -2
Vertex: (-2, -1)
x-intercepts: (-1,0) and (-3,0)
400
3. The following graph models the path of an object, in feet, being projected into the air. Answer the following questions using the model.
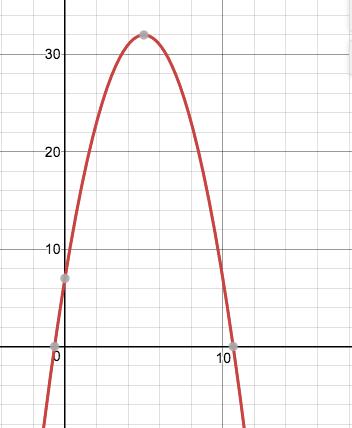
c) Was the object on the ground when it was projected into the air? How do you know?
No, the y-intercept shows that at time of 0 seconds, the object was 7 feet off the ground (y-intercept).
400
6. Dallin’s frisbee got stuck in a tree 14 feet from the ground. Dallin threw his shoe up at the frisbee to dislodge it. The height of the shoe is modeled by the equation h(t)= -16t2+25t+6 . Will the shoe go high enough to hit the frisbee? Defend your answer.
Yes, because if you calculate the maximum height, the maximum height is approximately 15.77 feet and will be able to reach the disc.
500
5. Rewrite y=2(x-3)2+7 in standard form. Identify the y-intercept.
Standard form:____________________
y-intercept:____________________
Standard form: y = 2x2 - 12x + 25
y-intercept: (0, 25)
500
Graph and identify each key feature
(100 points for each)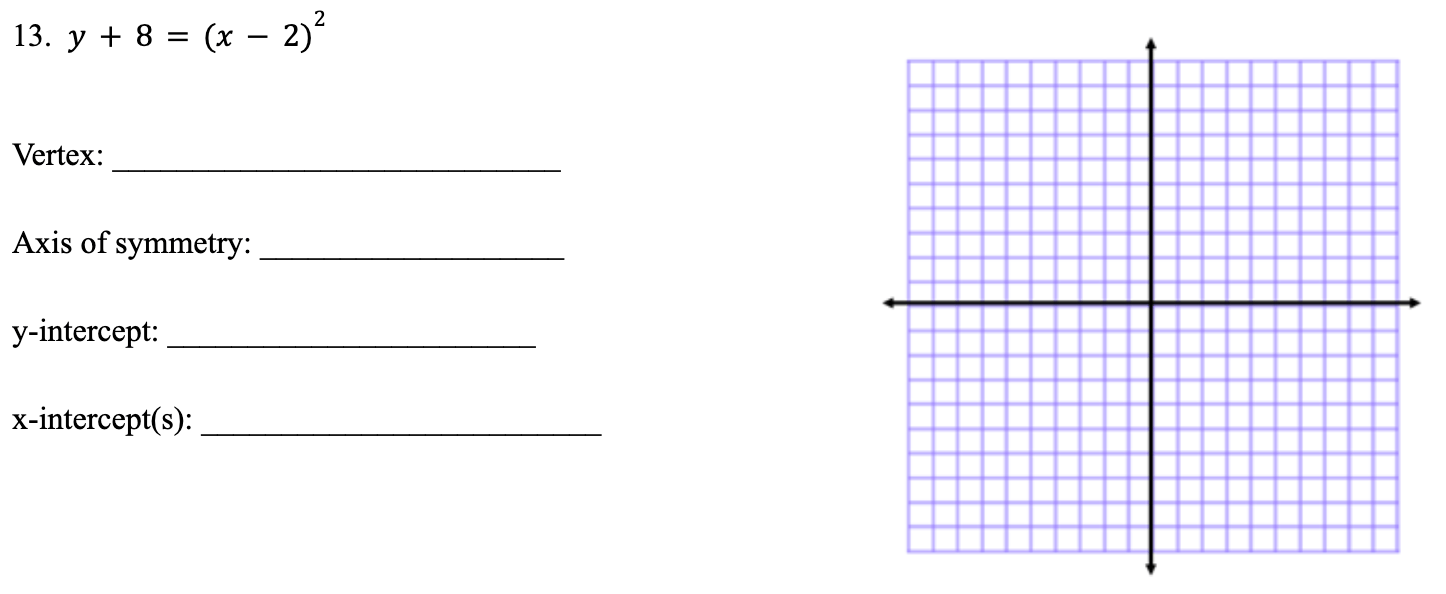
Vertex: (2, -8)
Axis of symmetry: x = 2
y-intercept: (0, -4)
(200 points) x-intercepts: (2+2sqrt2, 0) and (2-2sqrt2, 0)
500
1. The flight path of an arrow is modeled by the quadratic equation h(t)=-16t2+35t+5
a) Find its maximum height.
Approximately 24.14 feet
500
1. The flight path of an arrow is modeled by the quadratic equation h(t)=-16t2+35t+5
b) Find how long it was in the air.
Approximately 2.32 seconds