and Expressions
and
Inequalities
Is the following an example of correlation or causation?
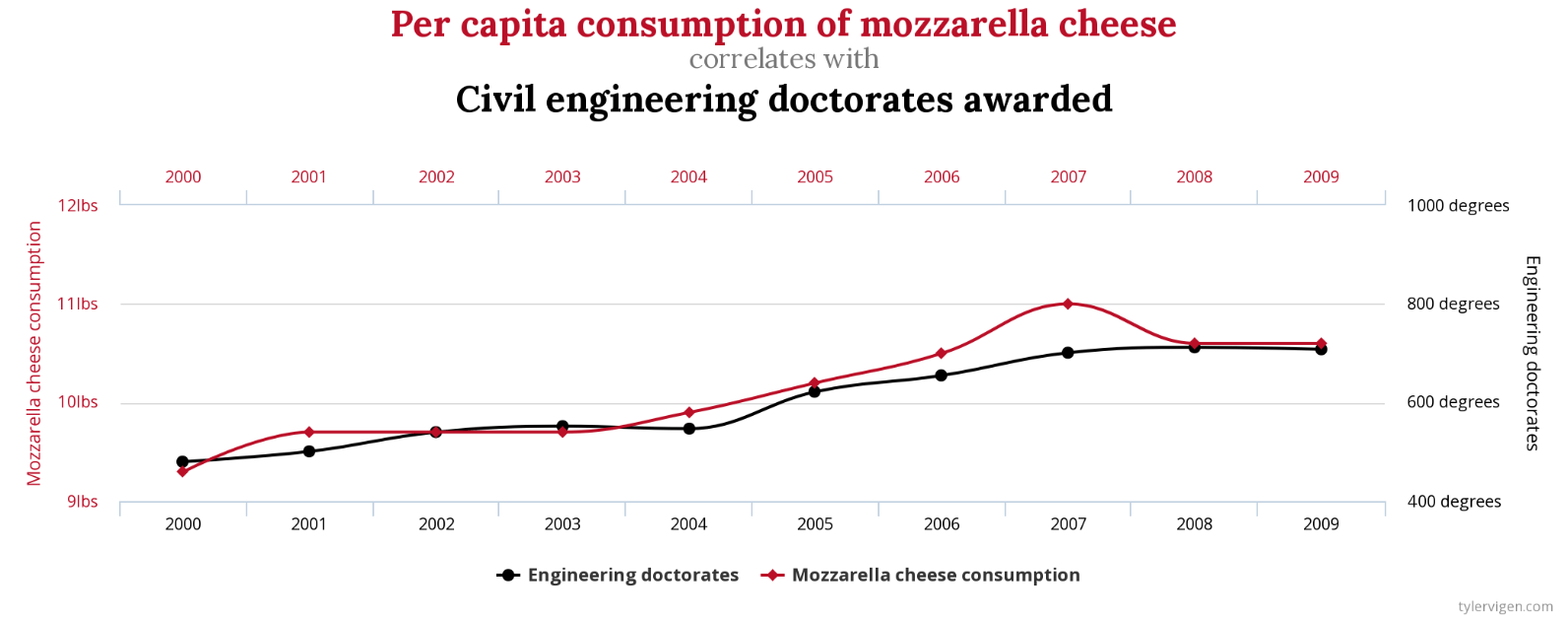
This graph is an example of correlation. Although there does appear to be a trend, there is no causal relationship between the two. In other words, the consumption of mozzarella cheese does not cause the change in number of civil engineering degrees.
This question is meant to demonstrate that correlation does NOT equal causation.
For imaginary numbers, what are the values for
i and i2
The values corresponding to i and i2 are:
i = sqrt(-1)
i^2 = -1
Determine whether each graph is a function or not:
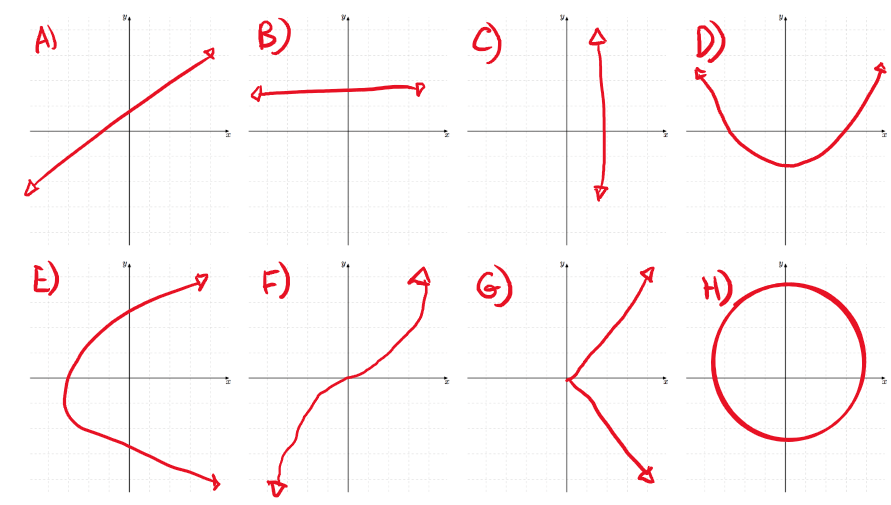
To determine which are and are not a function, we can use the vertical line test.

Which graph represents the inequality below
-9x+4y<=8
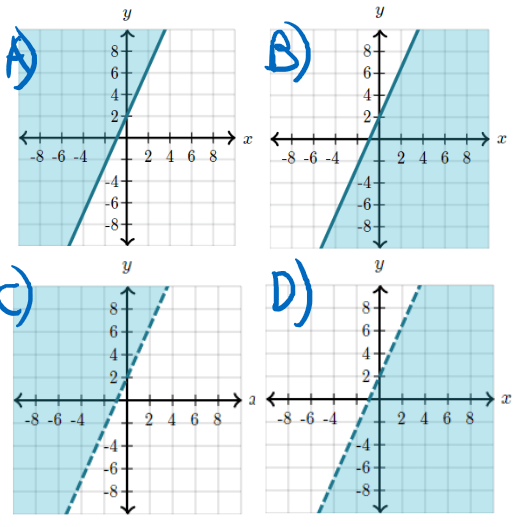
Since the inequality is a <=, the graph will have shading below the line and the line will be solid.
So the correct graph is graph B!
Write the inequality represented by the graph below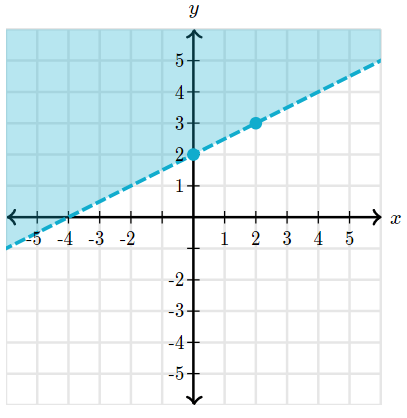
To find the inequality for this graph, we start by noticing the line is dotted and the shading is above the line, meaning we should use a > sign.
Next we can look at the two points (0,2) and (2,3) to find the slope.
(y_2-y_1)/(x_2-x_1)=(3-2)/(2-0)=(1/2)
So after noting that the y intercept is (0,2) we can write the inequality as
y>(1/2)x+2
Identify the type of equation (linear, exponential, quadratic, or none) of each graph below:
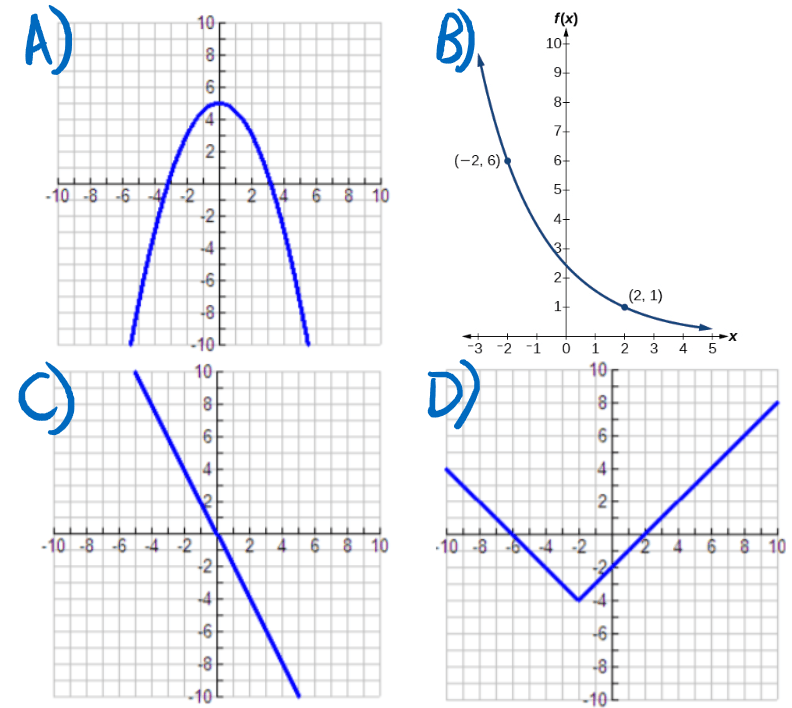
A) Since graph A is a parabola facing downward, we know that it must be a negative quadratic equation
B) Since graph B is a curve that appears to continue to decrease and flatten out, this graph is an exponential decay equation
C) Since graph C is a straight line decreasing from left to right, it is a decreasing linear equation
D) Since graph D has a point where two sides extend straight out and up, this is actually an absolute value equation so the answer is none or absolute value
Student radio asks its listeners to fill out a poll on their website to learn if they like the music played.
The poll showed that 87% of the 150 respondents "love" the music played on the radio.
What kind of bias does this example represent?
A) Response Bias
B) Undercoverage
C) Voluntary Response Sampling
The correct bias for this example is
C) voluntary response
This is because they asked listeners to participate, which means that the audience chose whether or not to participate.
Determine whether each number is rational or irrational :
1) sqrt(5)
2) 2pi
3) sqrt(64)
4) pi-1
Since irrational numbers are real numbers that cannot be written as a simple fraction...
1) irrational
2) irrational
3) rational
4) irrational
Evaluate the following function f at f(2):
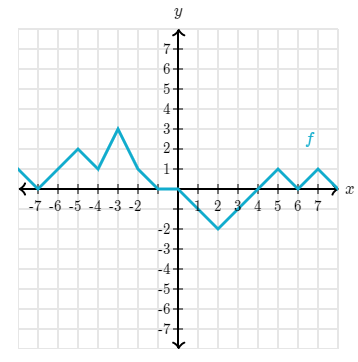
When we evaluate a function, we are finding the value of y when x is the given number.
When x = 2, the function is equal to -2.
So f(2)=-2
Solve the linear equation for x:
4x-9x=15
To solve this equation, first we simplify like terms and combine 4x and -9x
-5x=15
Then, we move the -5 over to get x by itself
x=(15/-5)=-3
So our answer is: x = -3
Which graph is a representation of the system of inequalities below:
y<3/4x+3
y<=-2x-1
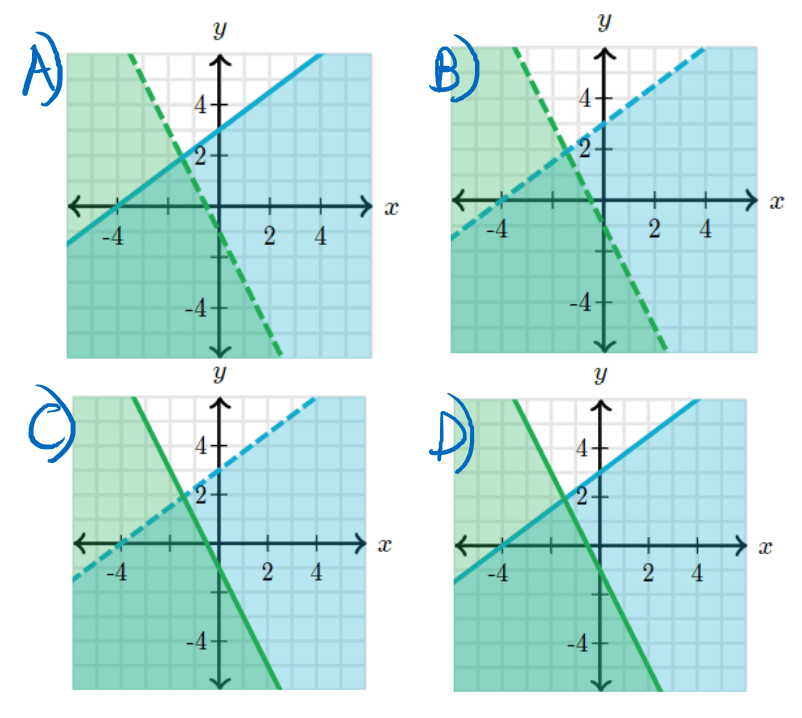
The best thing we can do to distinguish the graphs is look at the inequality signs used. Since the first equation has a less than but not equal to sign, the graph should be a dotted line that is shaded underneath it. For the second equation, we can see that we are using a less than or equal to sign so we need to use a solid line with shading underneath. The graph that shows this is graph C!
Use the zero product property to find the solutions to the following equation
(x+6)(-x+1)=0
To find the solutions, all we need to do is set each part equal to 0 and solve for x
(x+6)=0->x=-6
(-x+1)=0->x=1
Determine the type of correlation for each graph (positive, negative, or none)
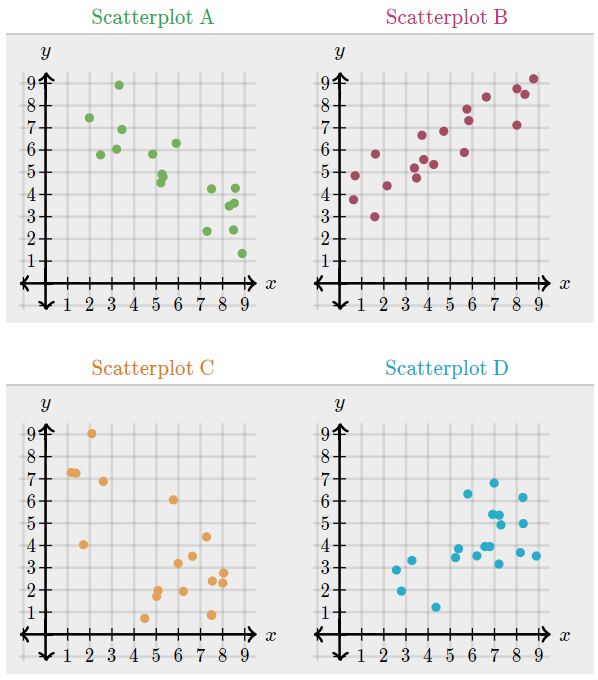
Scatterplot A is negative
Scatterplot B is positive
Scatterplot C is negative
Scatterplot D is positive
Determine the real and imaginary part of each complex number:
1)9i
2) 4-3i
3) 7i-2
4) -2
Since complex numbers are written as a + bi where a is the real part and b is the imaginary part. Therefore...
1) the real part is 0 and the imaginary is 9
2) the real part is 4 and the imaginary is -3
3) the real part is -2 and the imaginary is 7
4) the real part is -2 and the imaginary is 0
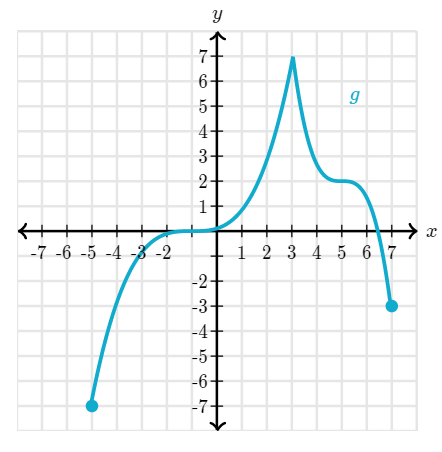
Evaluate the following according to the graph of f(x) and g(x)
5*f(1)+5*g(9)
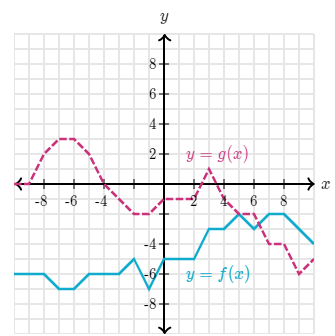
First we can use the graph to find the values of f(1) and g(9). Looking in the fourth quadrant, we can see that f(1) = -5, and g(9) = -6
Now we put those into our equation so
5*(-5)+5*(-6)=-55
Solve the linear inequality below, reduce any fractions to lowest terms and do not round.
-38d-57>=-19d+76
To start off, we'll move the terms with d to the left side and other terms to the right
-38d+19d>=76+57
From there we can combine like terms
-19d>=133
So once we divide both sides by -19 and switch which way the inequality sign is facing we find...
d<=-7
Find the system of equations and its solution for the given graph below
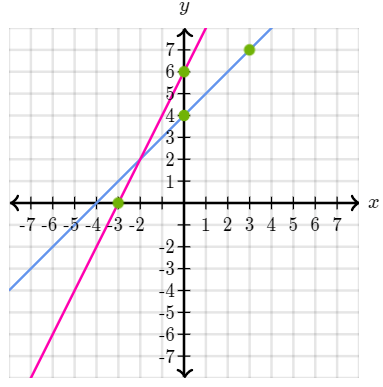
Looking at the graph we can use those two points per line to find the slope and the equation for each line.
y=2x+6,y=x+6
From there, it is easy to see the solution on the graph as it is the point where the lines intersect. The solution is:
x=-2,y=2
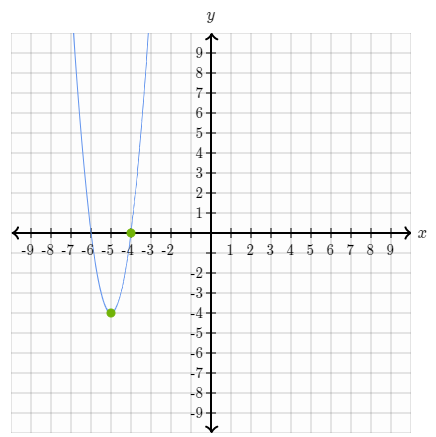
Graph the quadratic equation below and identify any x intercepts
y=4(x+6)(x+4)
Looking at this quadratic equation, we know from a=4 that our parabola is opening up and has a minimum of -4. From there, we find the zeroes of our equation to get our x intercepts:
(-6,0),(-4,0)
Match the following correlation coefficients to their graph:
1) -0.71 2) -0.92 3) 0.85 4) 0.39
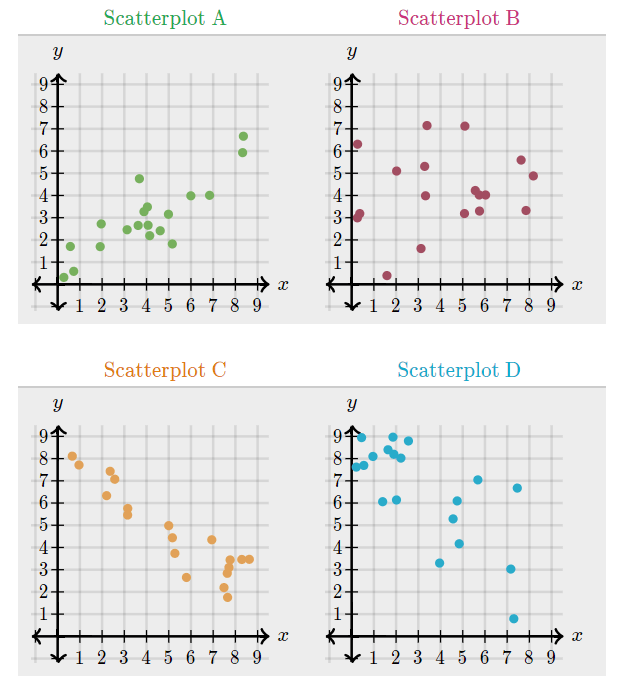
Scatterplot A has a correlation coefficient of: 0.85
Scatterplot B has a correlation coefficient of: 0.39
Scatterplot C has a correlation coefficient of: -0.92
Scatterplot D has a correlation coefficient of: -0.71
Which answer below is the simplified version of the given expression?
The correct answer is B,
(x+2)/(x^2+2x+4)
To get this answer, we first factor the top and bottom. The top equation becomes
(x^2-4) ->(x+2)*(x-2)
and the bottom becomes
(x^3-8)-> (x-2)*(x^2+2x+4)
What is the domain and range of the following graph? Put your answer in inequality notation.
If we look at our graph, we can determine the domain and range by examining the bounds of our x and then y variables.
for our domain:
-5<=x<=7
for our range:
-7<=y<=7
Rosie can complete 36 multiplication problems in 3 minutes. If she can keep up the pace, how many minutes (m) would it take for her to complete 54 problems?
To solve this problem, we can set up a proportion equation. We can use the info that she does 36 problems in 3 minutes.
(36/3)=(54/x)
We can use cross multiplication to find
(36x)=54*3
And then we finally solve it for x and get
x=4.5
So Rosie can complete 54 problems in 4.5 minutes!
Solve the following system of equations for x and y using elimination
-2x+15y=-24
2x+9y=24
Since we are solving this system using elimination, we are going to start but adding the two equations together
(-2x+2x)+(15y+9y)=(-24+24)
As we do that, enough terms cancel out to find y.
24y=0-> y=0
Since we now know what y is, we can plug it in to find x
-2x+15(0)=-24->-2x=-24->x=12
So the solution is x=12 and y=0
Does function A or function B fit the graph better?
Use that function to also predict the plant height in cm at 6 weeks after planting

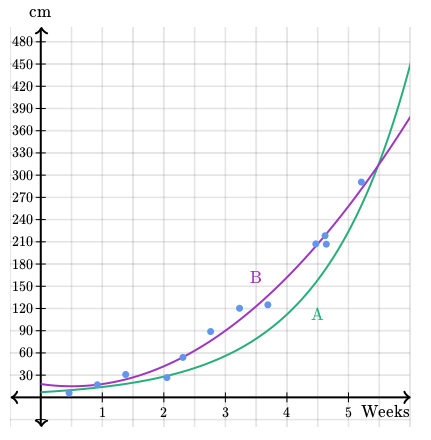
Function B is a better fit for this graph.
Knowing that, we substitute 6 weeks for x to get
y=12*(6)^2-12*(6)+18=378cm
Find the slope intercept form of the linear equation of the graph below:
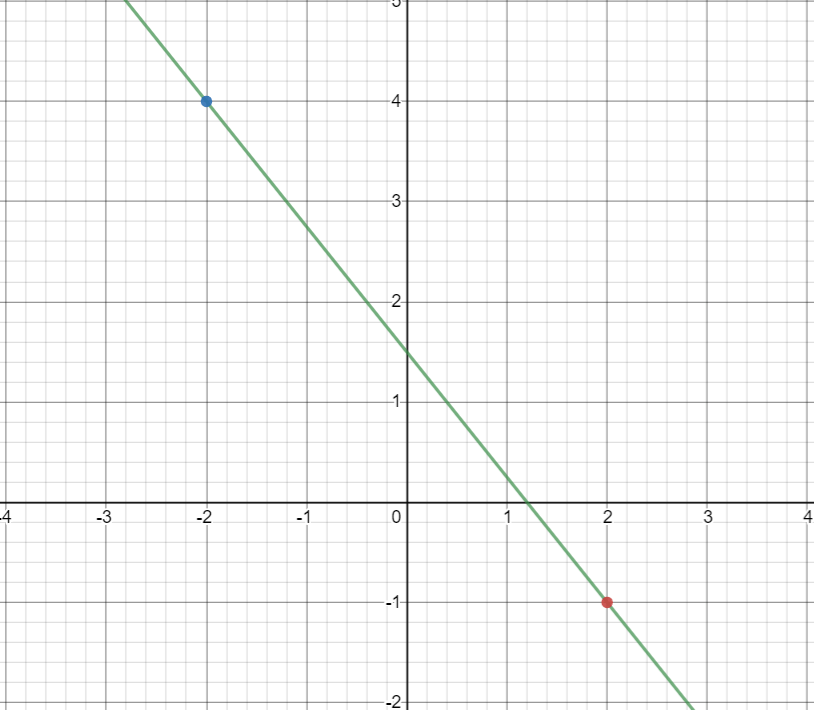
If we examine the graph we find that our two points are (-2,4) and (2,-1), which we can use to find the slope.
(y_2-y_1)/(x_2-x_1)=(-1-4)/(2--2)=(-5/4)
If we examine the graph again, we can see our y intercept is (0,1.5) which means our equation is:
y=(-5/4)x+1.5
The correct answer is C,
To simplify this equation, we should factor out a common term. All the numbers are multiples of 2 and have a x^3 term, so we'll factor that out.
2x^3*((1)/(1+2x^3))
For a school assignment, Rosie rides in the elevator of a local hotel and keeps track of the distance she travels up and down. Below is a graph of her altitude (in meters relative to the ground) as a function of time (in minutes).
Match the correct statement with the graph features: relative maximum or minimum, positive or negative interval, or increasing or decreasing interval.
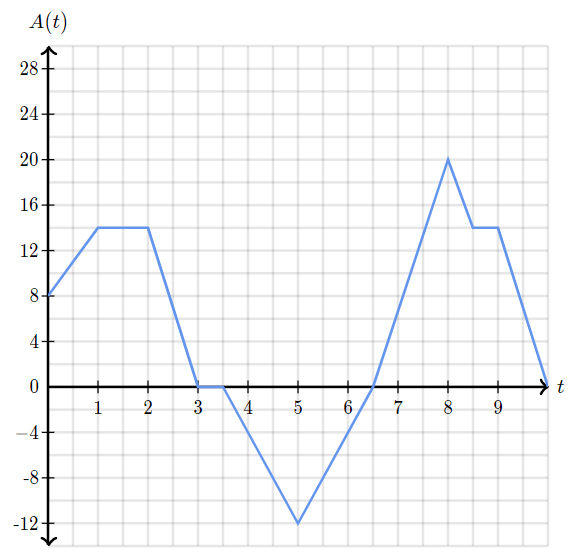
Statements:
A) Between the 6.5 and 10 minute marks, Rosie was above the ground
B) Between the 5 and 8 minute marks, the elevator was traveling upwards
C) Rosie's lowest altitude was 12 meters below the ground
Statement A's feature is a positive interval
Statement B's feature is an increasing interval
Statement C's feature is a relative minimum
Solve the following linear equation for y
4y-4=5y-8
To solve this linear equation, first we can move all our terms with y to the left and the rest to the right
4y-5y=-8+4
Next we combine like terms on both sides
-y=-4
Finally, we move the -1 over to the other side to get
y=4
Solve the following system of equations using substitution
6x-5y=15
x=y+3
To solve this system, since we have an equation for x we will substitute it into the first equation and simplify to find y
6(y+3)-5y=15->6y-5y+18=15->y=-3
From there, we can plug our y value back into the second equation to find the value of x
x=(-3)+3
So our final answer is:
x=0,y=-3
Solve the following quadratic for x by taking the square root
(x+5)^2-64=0
To find the solutions, we start to solve for x like normal
(x+5)^2=64->x+5=sqrt(64)
From there we recognize that in algebra we can't assume a square root gives a negative or a positive so we must represent both. So we split those up and solve for both
x+5=+8-> x=3
x+5=-8->x=-13
Find the slope intercept equation for the table of values below:
Rosie decides to drive home to visit her family before school starts. The trip is 350 miles and Rosie drives at a constant rate. Eager to get home, she keeps track of how many miles (y) were left to drive at a certain amount of time (x).
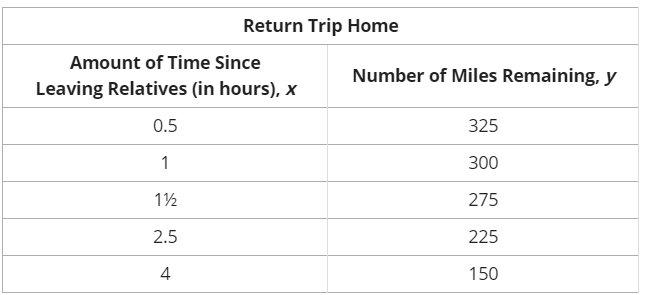
Our first step is to find the slope of the graph.We can do that by taking two of the points from the table.
(225-275)/(2.5-1.5)=-50/1
And the problem told us the trip is 350 miles so our y intercept is (0,350) so our equation is:
y=(-50)x+350
Simplify the following expression and state if there is a value that x cannot equal:
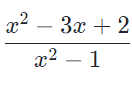
We first factor the numerator, which becomes
(x-2)*(x-1)
Then, we factor the denominator which becomes
(x+1)*(x-1)
Once we simplify that, we see our answer is
(x-2)/(x+1) when x!=1
A truck driver, Thomas, is driving across the country to deliver school supplies.
The graph below represents the fuel remaining in his gas tank (in liters) as a function of distance driven (in kilometers). According to the graph, how fast did his truck consume the fuel in its tank?
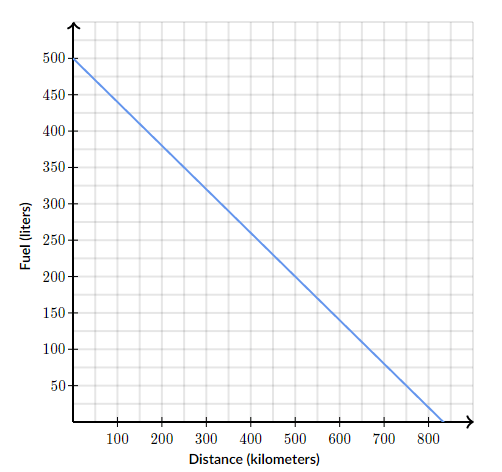
To find the rate of fuel consumption, we can pick two points on the graph and find the slope between them. Let's look at the points (0 km, 500 L) and (250 km, 350 L).
Using these two points, we can put them in the equation for slope to find the fuel consumption rate.
(y_2-y_1)/(x_2-x_1)=(350-500)/(250-0)=-(3/5)
So the truck consumes (-3/5) L per km
Solve the following linear inequality for x (use fractions reduced to the lowest terms)
54x+64>=49x+59
To solve this inequality, first we can move our x terms to the left side and all others to the right
54x-49x>=59-64
Next we combine like terms
5x>=-5
And finally, we move the 6 to the other side which gives us
x>=-1
Graph the following system of equations and use it to find the solution (use fractions if needed)
y=-x+2
y=3x-4
The graph should look like this:
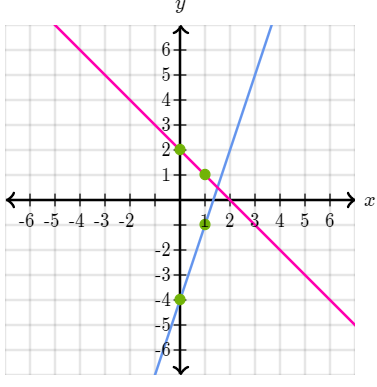
So then we can see the answer will be
x=3/2,y=1/2
Use the quadratic equation to solve the following quadratic for x
10x^2=6+9x
First, let's rearrange it so it looks like standard form
10x^2-9x-6=0
Now we just have to plug those values into the quadratic formula
x=(9+-sqrt((-9)^2-4(10)(-6)))/(2(10))
And finally we simplify to get
x=(9+-sqrt(321))/(20)